Вектори
Поняття вектора
Вектор – це направлений відрізок. Відповідно вектор так само як і відрізок має початок та кінець. Кінець вектора зображають стрілкою яка символізує напрям вектора.

Отже. Маємо вектори та Вектор так же як і відрізок може позначатися як двома великими літерами або однією маленькою латинського алфавіту.
Тут варто розуміти, що у випадку позначення маленькою літерою потрібно над нею ставити стрілку яка є символом вектора. Це варто робити як на малюнку так і у записах.
Якщо ж позначати великими літерами, то потрібно дотримуватися деяких правил:
На малюнку ми не ставимо стрілки над буквами. Також на малюнку буква, що стоїть біля стрілки є кінцем вектора, у нашому випадку це «В»; відповідно «А» це початок вектора.
При записі вектора з двома літерами першою йде літера, що символізує початок, а другою – кінець. Наший вектор є таким: Це є дуже важливим! Адже, та це абсолютно різні вектори!
Вектор початок та кінець якого збігаються, називають нульовим вектором. На малюнку такий вектор зображають точкою. Якщо його позначити якоюсь точкою, наприклад, «О», то даний нульовий вектор можна позначити як Нульовий вектор також позначають так Нульовий вектор не має напрямку.
Довжиною (також ще називають модулем або абсолютною величиною) вектора називають довжину відрізка. Наприклад, довжина вектора є довжина відрізка «АВ».
Модуль вектора позначають так: модуль вектора - так Довжина нульового вектора дорівнює нулю:
Вектори можуть бути однаково (або співнапрямленими) позначають символом та протилежно (або протилежно напрямленими) позначають символом напрямленими.
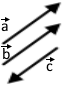
На малюнку вектори та є однаково направленими, а та чи та протилежно напрямленими.
Два вектори називаються рівними, якщо вони зміщуються паралельним перенесенням.
Говорячи простими словами, то вектори є рівними, якщо вони є однаково направлені та мають однакову довжину.

Вектор на площині
Найчастіше доводиться працювати із вектором на площині або у просторі. Розберемося, що це таке «вектор на площині».
Намалюємо вектор у Декартовій прямокутній системі координат.
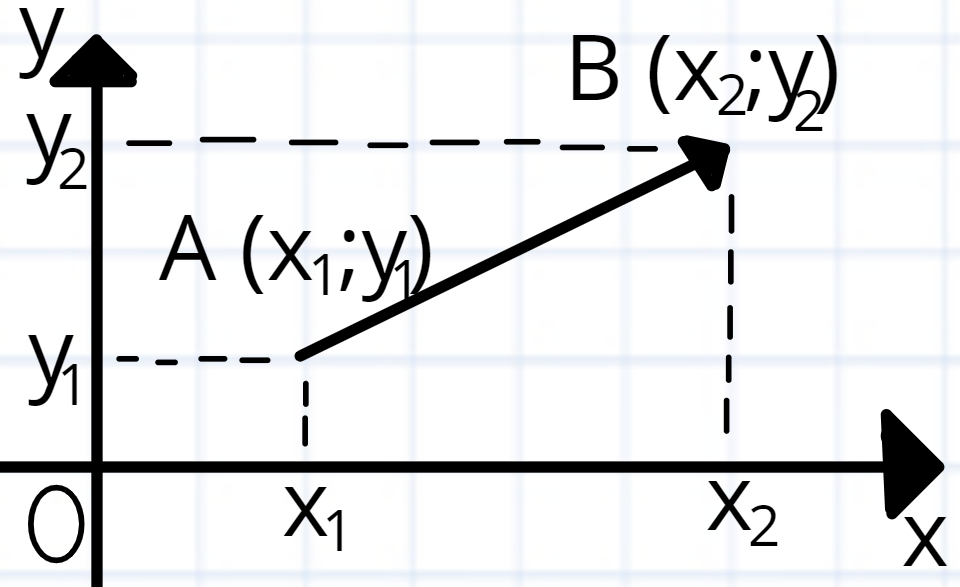
Отже, є вектор де початок вектора, кінець вектора. Як початок так і кінець мають свої координати відповідно.
У вектора також є свої координати. Їх шукають таким чином: від відповідних координат кінця вектора віднімають відповідні координати початку вектора.
- так шукають координати вектора за координатами його початку та кінця.
Деколи відразу дають координати вектора. Тому в таких випадках маємо відразу вектор з координатами: де та це по факту є
Довжину (модуль, абсолютну величину) вектора можна знайти за такою формулою:
|AB| = x2 + y2
Або
|AB| = (x2 - x1)2 + (y2 - y1)2
Дії з векторами
Сумою векторів та є вектор
Закони додавання векторів:
1. a + 0 = a
2. a + b = b + a
3. a + (b + c) = (a + b) + c
Різницею векторів та є вектор
Добуток вектора на число. Якщо є вектор який необхідно помножити на довільне число то в такому випадку необхідно кожну координату вектора помножити на це число.
λa(х; у) = a(λх; λу)
Закони множення вектора на число:
(λ + μ)a = λa + μa
λ(a + b) = λa + λb
|λa| = |λ|∙|a|
λa ↑↑ a, якшо λ > 0
λa ↑↓ a, якшо λ < 0
Наочне зображення векторів
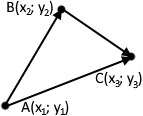
Сума. Правило трикутника. Якими б не були точки А, В, С підтверджується рівність:
«AB + BC = AC»
Сума. Правило паралелограма. Для векторів зі спільним початком їх сум зображується діагоналлю паралелограма, який побудований на цих векторах, до того ж початок вектора-суми збігається з початком цих векторів.
«AB + BC = AC»

Різниця. Правило для побудови різниці двох векторів. Щоб побудувати вектор, який дорівнює різниці векторів (від якого віднімаємо) і (який віднімаємо), треба від однієї точки відкласти вектори і що дорівнюють їм. Тоді вектор, початок якого збігається з кінцем вектора а кінець – з кінцем вектора буде різницею векторів і
«AB - AC = CB»
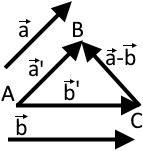
Множення вектора на число. Якщо вектор множиться на число, що є більшим за то вектор збільшить свої розміри. Якщо число є від до то зменшиться. Якщо число є від’ємне, то вектор змінить свій напрям на протилежний.
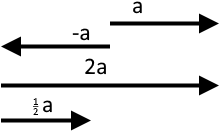
Колінеарні вектори. Рівні вектори
Колінеарними називають два ненульових вектори, які лежать на одній прямій, або на паралельних прямих.
Колінеарні вектори можуть бути однаково напрямленими або протилежно напрямленими.
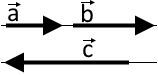
Два вектори називають рівними, якщо вони співнапрямлені і їх довжини рівні.
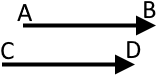
Якщо вектори колінеарні, то їх відповідні координати пропорційні. І навпаки, якщо відповідні координати двох векторів пропорційні, то ці два вектори колінеарні.
Тобто, якщо вектори та колінеарні, то Також можна записати так:
Розкладання вектора за двома неколінеарними векторами
Будь-який вектор можна розкласти за двома неколінеарними векторами і у вигляді до того ж це розкладання єдине.
Скалярний добуток векторів
Скалярним добутком векторів та називається число
Скалярний добуток двох векторів дорівнює добутку їх абсолютних величин на косинус кута між ними.
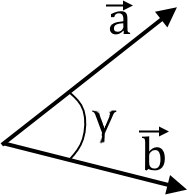
Властивості скалярного добутку векторів:
Для будь-яких векторів та числа виконуються рівності:
1. a ∙ b = b ∙ a
2. (λa ) ∙ b = λ(a ∙ b)
3. (a + b) ∙ c = a ∙ c + b ∙ c
4. a ∙ a = a2 = |a|2
5. a ∙ b = |a| ∙ |b| ∙ cosγ, де кут між векторами
6. Якщо a ∙ b = 0, то a ⊥ b
Якщо необхідно знайти кут між векторами, то варто скористатися властивістю скалярного добутку. Оскільки де кут між векторами та то виразивши косинус отримаємо:
cosγ = a ∙ b/|a||b|
Також можна цю формулу переписати через координати векторів. Для цього врахуємо, що: , , .
Отримаємо:
cosγ = x1 ∙ x2 + y1 ∙ y2/x12 + y12x22 + y22
А вже знаючи косинус кута між векторами, можна знайти цей кут (використовуючи таблицю або калькулятор).
Розглянемо декілька прикладів
1. Знайти координати вектора якщо
Отже, маємо вектор де - початок вектора, - кінець вектора. Щоб знайти координати вектора необхідно відняти від відповідних (від віднімаємо від - координат точки, що є кінцем вектора координати початку вектора:
AB(-1 -(-3); -2 -2) = AB(2; -4)
2. При якому значенні «x» скалярний добуток векторів і дорівнює
Нам відомо, що скалярний добуток двох векторів можна знайти так: Оскільки, скалярний добуток має бути рівним тобто
Як бачите в обох варіантах маємо однакову частину (в нашому випадку ліву), а якщо в двох прикладів є однакові частини, то дві інші частини рівні між собою.
Тобто Підставивши відповідні координати будемо мати:
1 ∙ 2x + (-1) ∙ 10 = 10
Після чого залишається розв’язати отримане рівняння. Це є лінійне рівняння. Як їх розв'язувати ви можете прочитати тут. А результат (відповідь) буде таким:
x = 10
3. Який з векторів та є колінеарним до
Колінеарними вектори є тоді, коли їх відповідні координати є пропорційними.
Перевіримо чи вектори є колінеарними.
- як бачимо при ділені відповідних координат поділити на а на виходять однакові числа. Це означає, що вектори є колінеарними.
Перевіримо чи вектори та є колінеарними.
- як бачимо при ділені відповідних координат поділити на а на виходять різні числа. Це означає, що вектори є неколінеарними.
4. При якому значенні вектори і перпендикулярні?
Вектори є перпендикулярними в тому випадку, коли їх скалярний добуток є рівним нулеві. Отже, коли Використавши, що то будемо мати Будемо мати:
1 ∙ 3 + 3 ∙ x = 0
Розв’язавши отримане рівняння будемо мати:
x = -1
5. Обчислити якщо - кут між векторами.
Скористаємося формулою пошуку скалярного добутку . Будемо мати:
a ∙ b = 5∙4∙cos600 = 10
6. Знайти кут між векторами «a(-2; 2)» і «b(-3; 0)».
Щоб знайти кут між векторами скористаємося формулою:
cos(a; b) = x1 ∙ x2 + y1 ∙ y2/x12 + y12x22 + y22
cos(a; b) = -2 ∙ (-3) + 2 ∙ 0/(-2)2 + 22(-3)2 + 02 = 6/62 = 1/2
Отже будемо мати, що бо «cos450 = 1/2».
7. Дано вектори «a(-2; 1)» і «b(3; -1)». Знайти координати вектора «n», якщо «n = 3a - 5b».
Для того щоб знайти вектор «n» необхідно знайти «3a» та «-5b» або «5b». Простими словами, необхідно помножити вектор на число. Тут варто зауважити на рахунок «-5b» або «5b». Якщо вектор «b» будемо множити на «-5», то після множення вектори «a» та «b» необхідно додавати, оскільки «-» вже буде врахований. А, якщо вектор «b» множити на «5», то вектори «a» та «b» необхідно буде віднімати, бо «-» не враховано.
Пам’ятаємо, якщо вектор множиться на число, то необхідно координати вектора помножити на це число.
Будемо мати:
3a(-2; 1) = a(-2∙3; 1∙3) = a(-6; 3)
-5b(3; -1) = b(3∙(-5); -1∙(-5)) = b(-15; 5)
Оскільки вектор «b» помножили на «-5», то вектори тепер необхідно додати. Пам’ятаємо, що при додаванні/відніманні необхідно додавати/віднімати відповідні координати.
n = a(-6; 3) + b(-15; 5) = n(-6+(-15); 3+5) = n(-21; 8)
8. Обчисліть скалярний добуток «(a - 2b)(a + b)», якщо «|a| = |b| = 2», «∠(a, b) = 600».
Для того щоб знайти скалярний добуток «(a-2b)(a+b)» в першу чергу розкриємо дужки:
(a - 2b)(a + b) = a ∙ a + a ∙ b - 2b ∙ a - 2b ∙ b
Тепер необхідно скористатися такими властивостями: «a ∙ a = a2 = |a|2», «a ∙ b = |a| ∙ |b| ∙ cos(a, b)», де «∠(a, b)» кут між векторами «a» та «b».
a ∙ a + a ∙ b - 2b ∙ a - 2b ∙ b = |a|2 + |a| ∙ |b| ∙ cos(a, b) - 2|b| ∙ |a| ∙ cos(a, b) - 2|b|2 = 22 + 2∙2∙½ - 2∙2∙2 - 2∙22 = -10