Багатокутники
Поняття багатокутника
Ламаною називається фігура, яка складається з точок та з’єднуючих їх відрізків Точки називаються вершинами ламаної, а відрізки - ланками ламаної.
Ламана називається простою, якщо вона не має самоперетинів.
Проста ламана
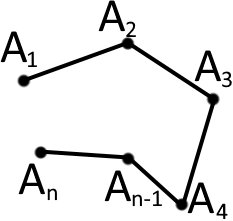
Ламана з самоперетинами
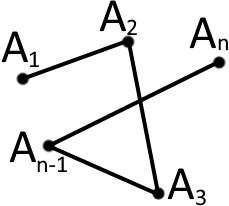
Ламана називається замкнутою, якщо у неї кінці співпадають.
Довжиною ламаної називається сума довжин її ланок.
Проста замкнута ламана називається багатокутником, якщо її сусідні ланки не лежать на одній прямій. Вершини ламаної називаються вершинами багатокутника, а ланки ламаної – сторонами багатокутника.

- багатокутник.
Дві сторони багатокутника називають сусідніми, якщо вони мають спільну вершину. та сусідні, оскільки у них є спільна вершина
Якщо ж сторони багатокутника не мають спільної вершини, їх називають не сусідніми. та не сусідні, оскільки у них не має спільної вершини.
Відрізки, які з’єднують не сусідні вершини багатокутника, називаються діагоналями. - діагоналі багатокутника.
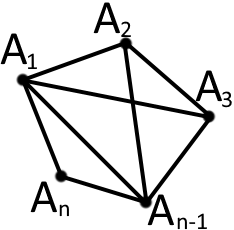
Діагоналі багатокутника
Кількість діагоналей можна знайти за формулою:
/n(n - 3)/2
Суму довжин усіх сторін багатокутника називають периметром багатокутника.
Найменше число сторін (а також вершин) багатокутника – три. У такому випадку маємо трикутник. Багатокутник з тобто з називається
Кути, що утворюються при сусідніх сторонах, називаються кутами багатокутника (внутрішніми). - кути багатокутника (внутрішні).
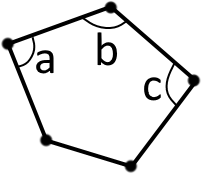
Кути багатокутника
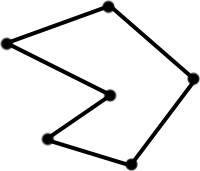
Багатокутник у якого всі кути є менші за розгорнутий (менші за градусів), називається опуклим.

Якщо хоча б один кут багатокутника є більшим за розгорнутий (за градусів), то такий багатокутник, називають неопуклим або випуклим.
Суму кутів (внутрішніх) опуклого n-кутника можна знайти так:
180°(n - 2)
Кути які є суміжними до кутів багатокутника (до внутрішніх кутів) називаються зовнішніми кутами багатокутника.
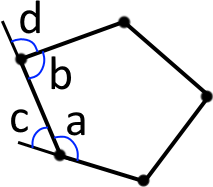
Сума зовнішніх кутів опуклого взятих по одному при кожній вершині, дорівнює градусів (завжди).
Правильним багатокутником називають опуклий багатокутник, у якого всі сторони рівні та всі кути рівні.
Позначимо через правильного
У такому випадку щоб знайти градусну міру внутрішнього кута правильного можна скористатися формулою:
αn = /180°(n - 2)/n
Цю формулу запам’ятати доволі просто. У чисельнику знаходиться формула суми всіх кутів багатокутника, а у знаменнику їх кількість.
Вписаний та описаний багатокутник
Багатокутник називається вписаним, якщо усі його вершини лежать на колі. При цьому кажуть, що коло є описаним навколо багатокутника.
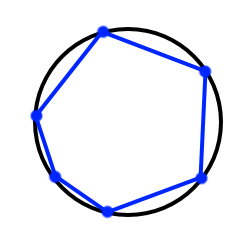
Багатокутник називається описаним, якщо усі його сторони є дотичними до кола. При цьому кажуть, що коло є вписаним у багатокутник.

Властивості правильного багатокутника
Якщо багатокутник правильний, то у нього можна вписати коло та навколо нього можна описати коло. При цьому центри вписаного та описаного кола збігаються.
Коло, вписане у правильний багатокутник дотикається до його сторін по середині.
У багатокутниках є формули, що пов’язують між собою сторону багатокутника та радіус вписаного/описаного кола. Розглянемо їх.
Будемо використовувати наступні позначення: правильного вписаного кола у правильний описаного кола навколо правильного
Сторону правильно можна знайти використавши радіус вписаного кола за допомогою формули:
an = 2r ∙ tg/180/n
З цієї формули радіус вписаного кола можна знайти так:
r = an2tg/180/n
Також сторону правильно можна знайти використавши радіус описаного кола за допомогою формули:
an = 2R ∙ sin/180/n
З цієї формули радіус описаного кола можна знайти так:
R = an2sin/180/n
Також ми можемо знайти радіус вписаного кола маючи при цьому радіус описаного кола:
r = R · cos/180/n
Та навпаки:
R = rcos/180/n
Розібрані приклади
Застосуємо теорію на практиці. Розберемо декілька прикладів:
Задача 1: Скільки всього діагоналей має десятикутник?
Кількість діагоналей n-кутника можна знайти за формулою:
/n(n - 3)/2
Де кількість вершин. Оскільки, ми маємо десятикутник, то В такому випадку будемо мати:
/10(10 - 3)/2 = 35
Отже, у десятикутника буде діагоналей.
Відповідь: 35.
Задача 2: Чому дорівнює сума внутрішніх кутів опуклого дванадцятикутника?
Суму внутрішніх кутів n-кутника можна знайти за формулою:
180°(n - 2)
Де кількість вершин. Оскільки, ми маємо дванадцятикутник, то В такому випадку будемо мати:
180°(12 - 2) = 1800°
Отже, сума внутрішніх кутів дванадцятикутника буде рівна
Відповідь: 1800°.
Задача 3: Скільки вершин має опуклий багатокутник, якщо сума його внутрішніх кутів дорівнює
Позначимо суму внутрішніх кутів як тоді матимемо
А суму внутрішніх кутів можна знайти за формулою:
180°(n - 2)
Тобто, ми будемо мати такий запис:
180°(n - 2) = an
Звідси, врахувавши матимемо:
180(n - 2) = 900
Отже, отримали лінійне рівняння зі змінною Розв’яжемо його:
180(n - 2) = 900 |∶180
n - 2 = 5
n = 5 + 2
n = 7
Отже, наший багатокутник буде мати вершин (кутів).
Відповідь: 7.
Задача 4: Чому дорівнює внутрішній кут правильного восьмикутника?
Позначимо через кількість кутів. За умовою задачі ми маємо восьмикутник, тому матимемо:
Градусну міру внутрішнього кута позначимо як
Для того щоб знайти градусну міру внутрішнього кута ми можемо скористатися формулою:
an = /180(n - 2)/n
Отже, будемо мати:
a8 = /180(8 - 2)/8
a8 = 135
Отже, внутрішній кут восьмикутника буде градусів.
Відповідь: 135.
Задача 5: Скільки сторін має правильний багатокутник, якщо його внутрішній кут дорівнює градусів?
Позначимо через кількість кутів. А через градусну міру внутрішнього кута багатокутника, матимемо:
Для того щоб кількість кутів багатокутника ми можемо скористатися формулою:
an = /180(n - 2)/n
Отже, будемо мати:
156 = /180(n - 2)/n
Ми маємо раціональне рівняння відносно змінної Детальніше читайте тут.
156 = /180(n - 2)/n |∙n
156n = 180(n - 2); n ≠ 0
156n = 180n - 360
156n - 180n = -360
-24n = -360 |∶(-24)
n = 15
Отже, багатокутник має вершин.
Відповідь: 15.
Задача 6: Скільки сторін має правильний багатокутник, якщо його зовнішній кут дорівнює градусів?
Враховуючи, що зовнішній кут має то позначимо його як і матимемо
Для того щоб знайти кількість сторін багатокутника нам варто знайти внутрішній кут багатокутника. Позначимо внутрішній кут як
Враховуючи, що внутрішній та зовнішній кут багатокутника є суміжними, то ми можемо скористатися властивістю, що сума суміжних кутів рівна Отже, матимемо:
a + b = 180
Підставимо значення та отримаємо лінійне рівняння відносно змінної
a + 20 = 180
a = 180 - 20
a = 160
Позначимо через «n» кількість кутів багатокутника.
Для того щоб кількість кутів багатокутника ми можемо скористатися формулою:
an = /180(n - 2)/n
Отже, будемо мати:
160 = /180(n-2)/n
Ми маємо раціональне рівняння відносно змінної Детальніше читайте тут.
160n = 180(n - 2); n ≠ 0
160n = 180n - 360
160n - 180n = - 360
-20n = -360 |∶(-20)
n = 18
Отже, багатокутник має вершин.
Відповідь: 18.
Задача 7: Кути п’ятикутника пропорційні до чисел Знайти ці кути.
Враховуючи, що ми маємо відношення п’яти чисел, то це означає, що ми матимемо п’ять вершин Використаємо такі позначення для цих кутів:
Тому ми будемо мати таке співвідношення:
Отже, ми будемо мати такі значення наших кутів:
a1 = 3x
a2 = 5x
a3 = 5x
a4 = 6x
a5 = 8x
Для того щоб знайти ці кути нам варто знайти суму всіх кутів. Скористаємося формулою:
180(n-2)
Матимемо:
180(5 - 2) = 540
Отже, сума всіх кутів багатокутника є рівною градусів. Після чого ми матимемо:
a1 + a2 + a3 + a4 + a5 = 540
Підставимо значення та отримаємо:
3x + 5x + 5x + 6x + 8x = 540
Розв’яжемо отримане рівняння:
27x = 540 |∶27
x = 20
Тепер знайдемо наші кути:
a1 = 3∙20 = 60
a2 = 5∙20 = 100
a3 = 5∙20 = 100
a4 = 6∙20 = 120
a5 = 8∙20 = 160
Відповідь: 60; 100; 100; 120; 160.
Задача 8: Сторона правильного шестикутника дорівнює Знайти його найбільшу діагональ.
Намалюємо правильний шестикутник сторін, Проведемо у ньому діагоналі і Також намалюємо описане коло навколо цього багатокутника.
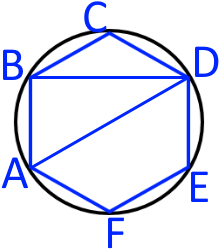
Як помітно у нас утворився прямокутний трикутник З гіпотенузою З властивості кола ми знаємо, що гіпотенуза прямокутного трикутника який вписаний у коло є одночасно діаметром і центр кола знаходиться по середині гіпотенузи.
Отже, щоб знайти довжину відрізка то нам необхідно знайти радіус описаного кола. Радіус описаного кола позначимо через врахувавши, що у нас є правильний шестикутник, то радіус зможемо знайти використавши формулу:
R = an2sin/180/n
Матимемо:
R = 102sin/180/6
R = 102sin 30
R = 10
Враховуючи, що сторона є діаметром, то нам необхідно помножити радіус на
AD = 2R
AD = 2 · 10 = 20
Відповідь: 20.
Задача 9: Радіус кола, вписаного в правильний шестикутник, дорівнює Знайти периметр шестикутника.
Нам необхідно знайти периметр. Оскільки, периметр це сума всіх сторін, а шестикутник у нас є правильним (тобто всі сторони рівні), то нам необхідно знайти будь-яку сторону.
Враховуючи, що ми маємо радіус вписаного кола (позначимо через то щоб знайти сторону (позначимо як можна скористатися формулою:
an = 2r ∙ tg/180/n
Отже, матимемо:
a = 2∙8√3∙tg/180/6
a = 16√3 ∙ tg 30
a = 16
Враховуючи, що шестикутник є правильним, то щоб знайти периметр можна помножити кількість сторін на довжину однієї. Матимемо:
P = 6a
P = 6 ∙ 16
P = 96
Відповідь: 96.
Задача 10: Скільки сторін має опуклий багатокутник, у якого сума внутрішніх кутів дорівнює сумі його зовнішніх кутів, узятих по одному при кожній вершині?
Враховуючи, що сума зовнішніх кутів багатокутника взятих по одному при кожній вершині завжди рівна градусів, то це означає, що сума внутрішніх кутів теж рівна градусів.
Оскільки, сума внутрішніх кутів чотирикутника рівна градусів, то відповідно наший багатокутник має сторони.
Відповідь: 4.
Задача 11: Скільки сторін має опуклий багатокутник, якщо сума всіх його внутрішніх кутів і всіх зовнішніх дорівнює «2520» градусів.
Для того щоб знайти кількість вершин можна скористатися формулою суми внутрішніх кутів:
180(n - 2)
Але на справді цю формулу можна сприймати як: «сума всіх кутів відняти суму зовнішніх кутів» Враховуючи цю умову ми можемо сказати, що суму всіх кутів (внутрішні + зовнішні) можна знайти так: Оскільки, нам ця сума є відома, то кількість кутів можна знайти так:
180n = 2520 |∶180
n = 14
Другий варіант розв’язання заключається в тому, що ми від загальної суми віднімаємо суму зовнішніх кутів, а потім застосовуємо формулу суми внутрішніх кутів багатокутника.
Відповідь: 14.
Задача 12: Скільки вершин має правильний багатокутник, у якого внутрішній кут у разів більший від зовнішнього?
Враховуючи, що ми маємо правильний багатокутник, то у нього всі внутрішні кути рівні між собою та зовнішні між собою. Позначимо зовнішній кут як а внутрішній як
У нашому випадку градусна міра зовнішнього кута є невідомою, тому позначимо її через
b = x
А внутрішній кут є у разів більший за зовнішній, тому матимемо:
a = 8b = 8x
Врахуємо, що зовнішній та внутрішній кут при одній вершині суміжними. Тому ми можемо скористатися властивістю, що сума суміжних кутів рівна
a + b = 180
Матимемо:
8x + x = 180
9x = 180 |∶9
x = 20
Отже, наші кути будуть:
a = 160
b = 20
Скористаємося формулою знаходження внутрішнього кута
an = /180(n - 2)/n
Матимемо:
160 = /180(n - 2)/n |·n
160n = 180(n - 2); n ≠ 0
160n = 180n - 360
160n - 180n = -360
-20n = -360 |∶(-20)
n = 18
Відповідь: 18.
Задача 13: Три кути багатокутника прямі, а решта дорівнюють по Скільки вершин має багатокутник?
В даному прикладі варто орієнтувати на суму зовнішніх кутів багатокутника. Оскільки вона завжди рівна то нам варто з’ясувати скільки необхідно кутів щоб отримати цю суму.
Врахуємо, що ми маємо три кути по тому ми маємо і три зовнішні кути теж (бо зовнішній та внутрішній кут при одній вершині є суміжними, а сума суміжних кутів рівна
Тому, ми маємо: градусів зайнятих.
Отже, залишилося ще градусів.
Оскільки, інші внутрішні кути є по то зовнішній кут при цій вершині буде Вийде, що нам необхідно ще три таких кути, бо
Отже, ми маємо три внутрішні кути по та три внутрішні кути по Звідси слідує, що ми маємо шестикутник.
Відповідь: 6.