Прямокутна система координат на площині.

Візьмемо на площині дві взаємноперпендикулярні прямі «х» та «у». Вісь «х» намалюємо горизонтально та зробимо на її правому кінці стрілочку («→»), а вісь «у» намалюємо вертикально і на її верхньому кінці теж поставимо стрілочку («↑»). Прямі «х» та «у» позначимо біля їх закінчень у вигляді стрілок. А в місці перетину поставимо точку «О».

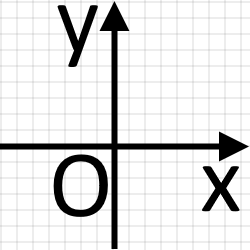
На малюнку зображена прямокутна Декартова система координат. Осі «х» та «у» називаються осями координат. Вісь «х» називають вісь абсцис також її ще позначають як «Ох», а вісь «у» називають вісь ординат також її ще позначають як «Оу». Точку «О» перетину осей координат називають початком координат.

Осі координат символізують послідовність чисел. А точка «О» є початком відліку. Тому, для осі «х», всі числа які є праворуч від точки «О» будуть додатними, а ліворуч від’ємними; для осі «у», всі числа які є над точкою «О» будуть додатними, а під нею від’ємними.

Також, така система координат ділить площину на чверті. Які мають свої порядкові номера, що рахуються проти руху стрілки годинника.

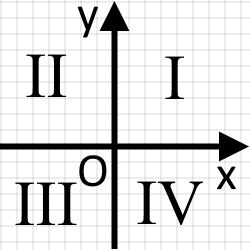
Їх називають координатними чвертями.

Кожна точка, що знаходиться на цій координатній площині має свої числові координати по осі «х» та «у». Ці координати записують у круглих дужках через крапку з комою, де першим йде координата по осі «х», а далі по осі «у»:

(х; у)

Для того щоб дізнатися координати якоїсь точки, необхідно, опустити (провести) перпендикуляр до кожної з осей.

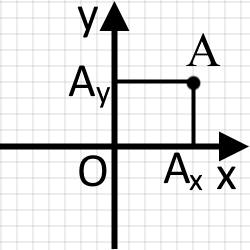
Так координатою точки «А» по осі «х» буде «A_x⁡⁡», а по осі «у» буде «A_y⁡⁡». Тоді ми будемо мати такий запис:

A(A_x⁡⁡; A_y⁡⁡)

Як помітно перед дужками ми поставили позначення (ім’я) нашої точки (тобто, точки «А»). Це необхідно для того щоб чітко розуміти в якої точки які координати.

У нашому випадку для позначення координат точки ми використали «A_x⁡⁡» та «A_y⁡⁡». Але якщо ми будемо вважати, що одна клітинка буде рівна одиниці, то координати точки «А» будуть такими:

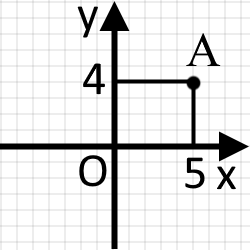
А(5; 4)

Не обов’язково вважати одну клітинку як одиницю. Наприклад можна вважати одну клітинку як трійку. В такому випадку матимемо:

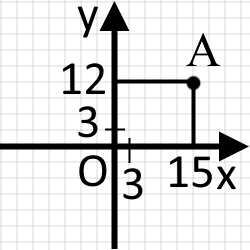
А(15; 12)

Якщо точка знаходиться на одній із координатних прямих, тоді координата по іншій прямій буде рівна нулеві. Наприклад, якщо точка знаходиться на осі «х», тоді координата по осі «у» буде рівна нулю, та навпаки, якщо точка знаходиться на осі «у», тоді координата по осі «х» рівна нулю.

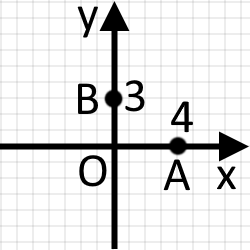
А(4; 0); В(0; 3)

Якщо точка знаходиться у початку координат, тоді її координатами по обох осях є нуль.

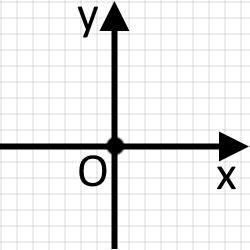
О(0; 0)

Формули для обчислення координат середини відрізка.

На координатній площині можуть знаходитися не лише точки, а і різноманітні фігури. Такі як: відрізок, пряма, коло і так далі.

Як ми вже знаємо, відрізок це є дві точки з’єднаних між собою. Маючи координати кінців цього відрізка ми без проблем можемо знайти координати його середини. Для цього нам необхідно буде додати відповідні координати («х» до «х». «у» до «у») кінців відрізка та поділити отриманий результат на «2».

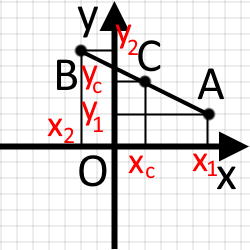
Маємо точки «А» та «В» які є кінцями відрізка «АВ», через точку «С» позначимо середину відрізка «АВ». Координати кінців відрізка будуть «A(x₁⁡⁡; y₁⁡⁡)», «B(x₂⁡⁡; y₂⁡⁡)», а координати точки «С» будуть «C(x_c⁡⁡; y_c⁡⁡)». В такому випадку координати середини відрізка ми зможемо знайти так:

x_c⁡⁡ = x₁⁡⁡ + x₂2

y_c⁡⁡ = y₁⁡⁡ + y₂2

Також, завдяки цим формулам ми можемо знайти координати будь-якого з кінців відрізка маючи координати іншого кінця та середини відрізка. Для цього нам необхідно помножити вирази на «2», після чого отримаємо:

x₁⁡⁡ + x₂⁡⁡ = 2x_c⁡⁡

y₁⁡⁡ + y₂⁡⁡ = 2y_c⁡⁡

І вже в залежності, що необхідно знайти варто буде розв’язати отримане рівняння (тобто підставити всі відомі числа і знайти, що залишиться).

Завдання 1: Знайти координати середини відрізка «АВ», якщо «A(-3; 2)», «B(-1; -2)».

Позначимо через точку «С» середину відрізка «АВ». А її координати будуть «C(x_c⁡⁡; y_c⁡⁡)». В такому випадку координати середини відрізка ми знайдемо за формулами:

x_c⁡⁡ = x₁⁡⁡ + x₂2

y_c⁡⁡ = y₁⁡⁡ + y₂2

Де «(x₁⁡⁡; y₁⁡⁡)» - координати першого кінця відрізка (наприклад точки «А»), «(x₂⁡⁡; y₂⁡⁡)» - координати другого кінця відрізка (наприклад точки «В»). Отже, матимемо:

x_c⁡⁡ = /-3 + (-1)/2 = /-4/2 = -2

y_c⁡⁡ = /2 + (-2)/2 = /0/2 = 0

Координати середини відрізка будуть такі:

C(-2; 0)

Завдання 2: Точка «С» є серединою відрізка «АВ». Знайти координати точки «В», якщо «А(-6; 7)», «С(-2; 2)».

Позначимо через «х» та «у» координати точки «В»: «В(х; у)».

Оскільки у нас є інший кінець відрізка (точка «А») та середина цього відрізка (точка «С»), то ми можемо скористатися формулами знаходження середини відрізка:

x_c⁡⁡ = x₁⁡⁡ + x₂2

y_c⁡⁡ = y₁⁡⁡ + y₂2

Де «(x₁⁡⁡; y₁⁡⁡)» - координати першого кінця відрізка (наприклад точки «А»), «(x₂⁡⁡; y₂⁡⁡)» - координати другого кінця відрізка (наприклад точки «В»). Отже, матимемо:

-2 = /-6 + x/2

2 = /7 + y/2

Ми отримали два лінійних рівняння. Перше відносно змінної «х», друге – «у». Розв’яжемо їх. Детальніше як розв’язувати лінійні рівняння читайте тут.

-2 = /-6 + x/2 |∙2

-4 = -6 + x

-6 + x = -4

x = -4 + 6

x = 2

2 = /7 + y/2 |∙2

4 = 7 + y

7 + y = 4

y = 4 - 7

y = -3

Отже, точка «В» буде мати такі координати:

B(2; -3)

Поділ відрізка в заданому відношенні.

Якщо точка «C(x₀⁡⁡; y₀⁡⁡)» поділяє відрізок «АВ» у відношенні «/AC/CB = k» (тобто, точка «С» не є серединою відрізка «АВ»), де «A(x₁⁡⁡; y₁⁡⁡)» і «B(x₂⁡⁡; y₂⁡⁡)», то координати точки «С» обчислюються за формулами:

x₀ ⁡⁡= x₁⁡⁡ + kx₂⁡⁡1 + k

y₀ ⁡⁡= y₁⁡⁡ + ky₂⁡⁡1 + k

Формула для обчислення відстані між двома точками із заданими координатами.

Якщо на координатній площині ми маємо точки «A(x₁⁡⁡; y₁⁡⁡)» та «B(x₂⁡⁡; y₂⁡⁡)», то відстань між двома точками ми можемо знайти за формулою:

AB = (x₁ ⁡⁡- x₂⁡⁡)²⁡ ⁡+ (y₁ ⁡⁡- y₂⁡⁡)²⁡⁡

Відстань між двома точками також ще називають довжиною відрізка у системі координат.

Завдання 1: Знайти довжину відрізка «АВ», якщо «А(-1; 2)» і «В(3; -1)».

Враховуючи, що ми маємо координати двох точок, то ми можемо знайти довжину між цими точками за формулою:

AB = (x₁ ⁡⁡- x₂⁡⁡)²⁡ ⁡+ (y₁ ⁡⁡- y₂⁡⁡)²⁡⁡

Де «(x₁⁡⁡; y₁⁡⁡)» - координати першої точки (наприклад точки «А»), «(x₂⁡⁡; y₂⁡⁡)» - координати другої точки (наприклад точки «В»). Отже, матимемо:

AB = (-1 - 3)²⁡⁡ + (2 - (-1))²⁡⁡ = (-4)² ⁡⁡+ (3)² = 16 + 9 = √25 = 5

Отже, відстань між точками «А» і «В» рівна «5».

Завдання 2: Знайти відстань від точки «А(-4; 3)» до початку координат.

Оскільки, нам необхідно знайти відстань від точки «А» до початку координат, то другою точкою у нас буде точка «О» з координатами «О(0; 0)». Для того щоб знайти відстань між ними ми можемо скористатися формулою:

AО = (x₁ ⁡⁡- x₂⁡⁡)²⁡ ⁡+ (y₁ ⁡⁡- y₂⁡⁡)²⁡⁡

Де «(x₁⁡⁡; y₁⁡⁡)» - координати першої точки (наприклад точки «А»), «(x₂⁡⁡; y₂⁡⁡)» - координати другої точки (наприклад точки «О»). Отже, матимемо:

AO = (-4 - 0)²⁡⁡ + (3 - 0)²⁡⁡ = (-4)² ⁡⁡+ (3)² = 16 + 9 = √25 = 5

Отже, відстань від точки «А» до початку координат рівна «5».

Завдання 3: Відстань між точками «А(2; 2)» і «В(-2; у)» дорівнює «5». Знайти значення «у».

Відстань між точками «АВ» рівна «5» («АВ = 5»). Для того щоб знайти значення «у» нам варто скористатися формулою:

(x₁ ⁡⁡- x₂⁡⁡)²⁡ ⁡+ (y₁ ⁡⁡- y₂⁡⁡)²⁡⁡ = AB

Де «(x₁⁡⁡; y₁⁡⁡)» - координати першої точки (наприклад точки «А»), «(x₂⁡⁡; y₂⁡⁡)» - координати другої точки (наприклад точки «В»). Отже, матимемо:

Підставивши значення будемо мати:

(2 - (-2))²⁡⁡ + (2 - y)² = 5

4²⁡⁡ + (2 - y)² = 5

16 + (2 - y)² = 5

Ми маємо ірраціональне рівняння. Детальніше про них читайте тут.

Для того щоб знайти «у» нам необхідно підняти обидві частини рівняння до квадрату. Так ми позбудимося кореня квадратного.

(16 + (2 - y)²)² = 5²

16 + (2 - y)²⁡ ⁡= 25

Перенесемо «25» у ліву частину рівняння при цьому змінимо знак на протилежний:

16 + (2 - y)²⁡⁡ - 25 = 0

(2 - y)²⁡ ⁡- 9 = 0

Розкриємо дужки використавши формулу скороченого множення «(a - b)²⁡⁡»:

4 - 4y + y²⁡ ⁡- 9 = 0

y² ⁡⁡- 4y - 5 = 0

Отримали квадратне рівняння. Детальніше про як їх розв’язувати читайте тут.

D = (-4)² ⁡⁡- 4∙1∙(-5) = 16 + 20 = 36

y₁⁡⁡ = /-(-4) + √36/2 ∙ 1 = /4 + 6/2 = 5

y₂⁡⁡ = /-(-4) - √36/2 ∙ 1 = /4 - 6/2 = -1

Отже, ми отримали два значення «у»:

y₁⁡⁡ = 5

y₂⁡⁡ = -1

Відстань від точки до осі.

У випадках коли нам необхідно знайти відстань від точки до будь-якої осі, то ця відстань буде рівна координаті точки відносно іншої осі.

Якщо ми маємо точку «А» з координатами «A(x₀⁡⁡; y₀⁡⁡)», то відстань від цієї точки до осі «х» буде рівна «y₀⁡⁡», а до осі «у» буде рівна «x₀⁡⁡». Оскільки це будуть довжини перпендикулярів проведених з даної точки до осей.

Рівняння прямої.

Рівняння прямої в прямокутній системі координат має вигляд:

ax + by + c = 0

Де «a», «b», «c» - довільні числа, причому «a» і «b» одночасно не можуть бути рівними нулю.

Рівняння «ax + by + c = 0» називають загальним рівнянням прямої.

Також часто зустрічається рівняння такого вигляду:

y = kx + p

Дане рівняння можна отримати, якщо з рівняння «ax + by + c = 0» виразити «у». Тобто:

by = -ax - c

Розділимо на «b»:

by = -ax - c |∶b

y = -/a/bx - /c/b

Та скористаємося заміною: «-/a/b = k», «-/c/b = p». Після чого отримаємо рівняння:

y = kx + p

У такому рівнянні «k» називають кутовим коефіцієнтом, також це є тангенсом кута, який утворює ця пряма з додатним напрямом осі «х» (з віссю «Оу»); «p» це є координата перетину прямої з віссю «у» (з віссю «Оу»).

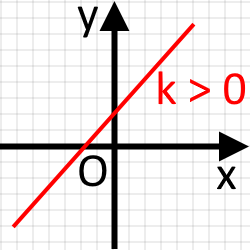
В залежності від знаку «k» наша пряма буде мати різний нахил.

При «k > 0» лівий край прямої буде нижчий за правий. І дана пряма буде утворювати гострий кут із додатним напрямом осі «х».

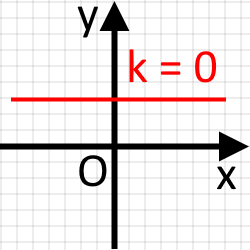
При «k = 0» пряма буде паралельною до осі «х» (до «Ох»).

При «k < 0» лівий край прямої буде вищий за правий. І дана пряма буде утворювати тупий кут із додатним напрямом осі «х».

Звідси отримаємо умову паралельності прямих: якщо дві прямі заданні рівняннями «y = k₁⁡⁡x + p» і «y = k₂⁡⁡x + p», то ці прямі будуть паралельними тоді і тільки тоді, коли їх кутові коефіцієнти є рівними. Тобто, при «k₁ ⁡⁡= k₂⁡⁡».

Також ми можемо записати рівняння прямої, що проходить через точки «A(x₁⁡⁡; y₁⁡⁡)» і «B(x₂⁡⁡; y₂⁡⁡)», якщо «x₁⁡⁡ ≠ x₂⁡⁡» і «y₁⁡⁡ ≠ y₂⁡⁡»:

x - x₁x₂⁡⁡ - x₁ = y - y₁y₂⁡⁡ - y₁⁡⁡

Рівняння прямої, що має кутовий коефіцієнт «k» і проходить через точку «A(x₀⁡⁡; y₀⁡⁡)» має вигляд:

y - y₀ ⁡⁡= k(x - x₀⁡⁡)

Або

y = y₀⁡ ⁡+ k(x - x₀⁡⁡)

Завдання 1: Складіть рівняння прямої, яка проходить через точки «А(1; -3)» і «В(-2; -9)».

Оскільки нам відомо дві точки і необхідно скласти рівняння прямої, то варто скористатися формулою:

x - x₁x₂⁡⁡ - x₁ = y - y₁y₂⁡⁡ - y₁⁡⁡

Де «(x₁⁡⁡; y₁⁡⁡)» це координати точки «A(1; -3)», а «(x₂⁡⁡; y₂⁡⁡)» координати точки «B(-2; -9)». Матимемо:

/x - 1/-2 - 1 = /y - (-3)/-9 - (-3)

/x - 1/-3 = /y + 3/-6

Скористаємося метеликом. Детальніше читайте тут.

-6(x - 1) = -3(y + 3)

Перенесемо все в одну часину:

-6(x - 1) + 3(y + 3) = 0

Та розкриємо дужки:

-6x + 6 + 3y + 9 = 0

-6x + 3y + 15 = 0

Отримали рівняння прямої вигляду: «ax + by + c = 0». Давайте ще складемо рівняння прямої вигляду: «y = kx + p».

Для цього необхідно виразити «у». Перенесемо все крім «3у» у протилежну частину:

3y = 6x - 15

І щоб звільнити «у» нам необхідно поділити весь вираз на «3».

3y = 6x - 15 |∶3

y = 2x - 5

Отже, отримали рівняння прямої вигляду: «y = kx + p».

Завдання 2: Складіть рівняння прямої, яка проходить через точку «А(-4; 3)» і паралельна прямій «у = 0,5х - 4».

В першу чергу нам варто зауважити, що пряма рівняння якої ми маємо скласти є паралельною до прямої «у = 0,5х - 4». Це означає, що їх кутові коефіцієнти є рівними. Тому в нашому рівнянні кутовий коефіцієнт буде рівний «0,5», тобто «k = 0,5».

Отже, виходить, що ми маємо кутовий коефіцієнт прямої та точку через яку ця пряма проходить. Звідси слідує, що ми можемо скористатися формулою:

y = y₀ ⁡⁡+ k(x - x₀⁡⁡)

Де «(x₀⁡⁡; y₀⁡⁡)» це координати точки через яку проходить наша пряма. Тобто, координати точки «A(-4; 3)».

Будемо мати:

y = 3 + 0,5(x - (-4))

y = 3 + 0,5(x + 4)

Розкриємо дужки:

y = 3 + 0,5x + 2

y = 0,5x + 5

Отже, ми отримали рівняння прямої вигляду: «y = kx + p».

Рівняння кола.

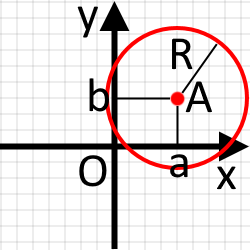
Рівняння кола з центром у точці «A(a; b)» та радіусом «R» («R > 0») має вигляд:

(x - a)² ⁡⁡+ (y - b)²⁡⁡ = R²⁡⁡

Завдання 1: Скласти рівняння кола, діаметром якого є відрізок «АВ», якщо «А(-5; 9)», «В(7; -3)».

Для того щоб скласти рівняння кола нам необхідно знати координати центру цього кола та радіус цього кола. За умовою задачі нам сказано, що «АВ» є діаметром цього кола. Тому центр кола буде мати координати середини відрізка «АВ». А радіус кола буде рівний половині довжини відрізка «АВ».

Знайдемо координати середини відрізка «АВ». Припустимо, що ц буде точка «С» з координатами «C(x₀⁡⁡; y₀⁡⁡)». Тоді, ми можемо знайти середину відрізка скориставшись формулами:

x_c⁡⁡ = x₁⁡⁡ + x₂2

y_c⁡⁡ = y₁⁡⁡ + y₂2

Де «(x₁⁡⁡; y₁⁡⁡)» - координати першої точки (наприклад точки «А»), «(x₂⁡⁡; y₂⁡⁡)» - координати другої точки (наприклад точки «В»). Отже, матимемо:

x_c⁡⁡ = /-5 + 7/2 = 1

y_c⁡⁡ = /9 + (-3)/2 = 3

Отже, координати середини відрізка та центру кола будуть: «С(1; 3)».

Для того щоб знайти радіус ми можемо знайти довжину відрізка «АВ» та поділити її на два або можна знайти довжину відрізка «АС» чи «ВС».

Знайдемо довжину відрізка «АС» скориставшись формулою:

AC = (x₁ ⁡⁡- x₂⁡⁡)²⁡ ⁡+ (y₁ ⁡⁡- y₂⁡⁡)²⁡⁡

Але оскільки у формулі рівняння кола використовується радіус в квадраті, то ми можемо відразу шукати довжину відрізка в квадраті:

AC²⁡⁡ = (x₁⁡⁡ - x₂⁡⁡)²⁡⁡ + (y₁⁡⁡ - y₂⁡⁡)²⁡⁡

Де «(x₁⁡⁡; y₁⁡⁡)» - координати першого кінця відрізка (наприклад точки «А»), «(x₂⁡⁡; y₂⁡⁡)» - координати другого кінця відрізка (наприклад точки «С»). Отже, матимемо:

AC²⁡⁡ = (-5 - 1)²⁡⁡ + (9 - 3)²⁡⁡ = (-6)²⁡⁡ + (6)²⁡⁡ = 36 + 36 = 72

Отже, остаточно ми будемо мати таке рівняння кола:

(x - 1)²⁡⁡ + (y - 3)²⁡⁡ = 72

Завдання 2: Вказати центр радіус кола «x²⁡⁡ + y²⁡⁡ + 16y + 60 = 0».

У таких завданнях необхідно користуватися формулами скороченого множення: «(a + b)²⁡⁡» або «(a - b)²⁡⁡». Для цього варто виділити повний квадрат, тобто вирази «a² ⁡⁡+ 2ab + b²⁡⁡» або «a² ⁡⁡- 2ab + b²⁡⁡».

Як помітно у нас є число з «x²⁡⁡» але не має числа з «х», тому повний квадрат тут не добудиться і вираз з «х» ми не зачіпаємо. А вираз з «у» ми зможемо перетворити. Як помітно у нас вже є «y² ⁡⁡+ 16y», тобто ми маємо «a² ⁡⁡+ 2ab», де «y²⁡⁡ = a²⁡⁡» і «16y = 2ab». Тобто, ми будемо мати, що «2 ∙ y ∙ 8 = 2ab». Звідси слідує, що «b = 8».

Отже, до виразу «y²⁡⁡ + 16y» нам не вистачає «+ 64» (бо «b²⁡⁡ = 8² ⁡⁡= 64»), тому допишемо його. Але щоб все наше рівняння не змінилося нам варто зробити протилежну дію. Тобто, ще написати «- 64». Отже, будемо мати:

x² ⁡⁡+ y²⁡⁡ + 16y + 64 - 64 + 60 = 0

Після чого скористаємося формулами скороченого множення:

x² ⁡⁡+ (y + 8)²⁡ ⁡- 64 + 60 = 0

x²⁡⁡ + (y + 8)²⁡ ⁡- 4 = 0

Перенесемо «-4» у протилежну сторону та отримаємо:

x² ⁡⁡+ (y + 8)²⁡⁡ = 4

Оскільки, поруч з «x²⁡⁡» не має ні якого числа, то координата центру кола по осі «х» буде рівна «0», а по осі «у» ми будемо мати «-8» (не забуваємо, що у загальному вигляді рівняння кола в дужках стоїть знак мінус, тому ми маємо брати число з протилежним знаком). Звідси слідує, що центр кола буде мати координати: «(0; -8)».

А щоб знайти радіус кола необхідно добути корінь з «4». Матимемо: «R = √4 = 2».