Для того щоб успішно розв’язувати практичні завдання вам варто ознайомитися з теоретичним матеріалом. Це можна зробити тут i тут.

Задача 1: Одна зі сторін трикутника дорівнює «7» см. Знайти висоту, проведену до цієї сторони, якщо площа трикутника дорівнює «35» см².

Оскільки за умовою задачі нам відома площа трикутника, то ми можемо використовувати формули які зв’язані з площею. Наприклад в цьому випадку зручно використати таку формулу:

S = ah_a2

Де «S» - площа трикутника, «a» - сторона трикутника, «h_a» - висота яка проведена до обраної сторони.

Тобто з цієї формули ми зможемо відразу знайти висоту.

h_a = /2S/a

Підставимо все що нам є відомо:

h_a = /2 ∙ 35/7

Оскільки, після підстановки ми відразу можемо знайти висоту (бо лише вона є невідомою), то залишається просто обчислити її значення.

h_a = 10

Відповідь: 10 см.

Задача 2: Градусні міри кутів трикутника відносяться як «3 : 2 : 10». Знайти градусну міру найменшого кута трикутника.

Позначимо кути трикутника так: «І» - перший кут, «ІІ» - другий кут, «ІІІ» - третій кут.

За умовою задачі нам відоме їх співвідношення «І : ІІ : ІІІ = 3 : 2 : 10». Тому ми можемо записати, що наші кути будуть такими: «І = 3х», «ІІ = 2х», «ІІІ = 10х». Коли є співвідношення то беруться по черзі вирази з лівої та з правої частини і там де є звичайні числа дописуємо змінну «х». Вона є множником пропорції.

Для того щоб знайти градусну міру найменшого кута необхідно знайти градусні міри всіх кутів. Для цього нам необхідно знайти «х». Скористаємося властивістю кутів трикутника: сума всіх внутрішніх кутів трикутника рівна «180» градусів. Тобто:

I + II + III = 180

Якщо ми підставимо замість «І», «ІІ», «ІІІ» наші вирази з «х», то отримаємо:

3х + 2х + 10х = 180

Отже, отримали лінійне рівняння яке залишається розв’язати:

15х = 180

х = 180 : 15

х = 12

Після чого залишається підставити замість «х» «12» у наші вирази «І = 3х», «ІІ = 2х», «ІІІ = 10х». Оскільки у «ІІ» є найменше число поруч з «х», то відповідно там буде найменший кут (ви щоб переконатися можете підставити у всі вирази та обчислити їх).

ІІ = 2 ∙ 12 = 24

Відповідь: 24 градуси.

Задача 3: У трикутнику «АВС» кут «А = 30 градусів», кут «В = 105 градусів». Знайти відношення «ВС : АВ».

Намалюємо наший трикутник:

Як видно з малюнку сторона «АВ» знаходиться навпроти кута «С», а сторона «ВС» навпроти кута «А».

У трикутнику маючи дві сторони та кути, що знаходяться навпроти них можна скористатися теоремою синусів. Будемо мати:

/BC/sin ⁡A = /AB/sin ⁡C

Звідси ми можемо знайти відношення «ВС : АВ». Скориставшись метеликом, отримаємо:

/BC/AB = /sin⁡ A/sin ⁡C

Але нам не відомий кут «С». Його можна знайти за властивістю внутрішніх кутів трикутника. Оскільки сума внутрішніх кутів трикутника рівна «180» градусів, то матимемо:

∠A + ∠B + ∠C = 180

Підставимо все, що нам відомо:

30 + 105 + ∠C = 180

Отримали лінійне рівняння з невідомою «∠C». Залишається його розв’язати:

135 + ∠C = 180

∠C = 180 - 130

∠C = 45

Тепер у нас є всі данні. Підставимо «30» замість «А», «45» замість «С».

/BC/AB = /sin⁡ 30/sin⁡ 45

/BC/AB = sin⁡ 30 ∶ sin ⁡45

/BC/AB = /1/2 ∶ /1/√2

/BC/AB = /1/2 · /√2/1

/BC/AB = /√2/2

Відповідь: /√2/2.

Задача 4: Дві сторони трикутника дорівнюють «48» см і «28» см. Указати всі можливі значення периметра трикутника.

Припустимо, що у трикутнику є сторони «a», «b», «c». Периметр «Р» трикутника можна знайти додавши всі сторони. Тобто:

P = a + b + c

За правилом трикутника кожна сторона є більшою за модуль різниці двох інших сторін (оскільки довжина сторони не може бути від’ємною, тому ми беремо результат по модулю) та меншою за їх суму.

Візьмемо, що сторона «a» буде мати довжину «48», сторона «b» матиме довжину «28». Тому в такому випадку довжина сторони «с» буде така:

|a - b| < c < a + b

Підставимо наші значення та знайдемо можливі варіанти довжини сторони «с».

|48 - 28| < c < 48 + 28

20 < c < 76

Ми отримали можливі варіанти довжини сторони «с». Оскільки не відома точна довжина, то і периметр може бути також приблизним. Його довжина може бути в межах від найменшого значення сторони «c_min» до найбільшого «c_max».

a + b + c_min < P < a + b + c_max

Отже, маємо:

48 + 28 + 20 < P < 48 + 28 + 76

96 < P < 152

Відповідь: 96 < P < 152.

Задача 5: Периметр трикутника дорівнює «50», а його бісектриса ділить протилежну сторону на відрізки завдовжки «15» і «5». Знайти меншу сторону.

Візьмемо трикутник «АВС» та проведемо у ньому бісектрису «ВН». Намалюємо цей трикутник:

Відрізки «АН» та «СН» утворилися при проведені до сторони «АС» бісектриси «ВС».

Візьмемо, що відрізок «АН» буде мати довжину «15», а відрізок «СН» матиме довжину «5». Тоді сторона «АС» буде мати довжину:

АС = АН + СН

АС = 15 + 5 = 20

В такому випадку на сторони «АВ» та «ВС» залишається «Р – АС». Тобто будемо мати:

АВ + ВС = Р - АС

АВ + ВС = 50 - 20

АВ + ВС = 30

Якщо, ми візьмемо, що сторона «ВС» буде мати довжину «х», то сторона «АВ» буде мати довжину:

АВ + х = 30

АВ = 30 - х

Нам важливо було переписати наші сторони через одну змінну. Можна було переписати сторону «АВ» або «ВС» через одну з них. Тобто «АВ» через «ВС» чи навпаки.

За властивістю бісектриси ми можемо скласти таке співвідношення:

/AB/AH = /BC/CH

/30 - x/15 = /x/5

5(30 - x) = 15x

150 - 5x = 15x

15x + 5x = 150

20x = 150

x = /150/20

x = 7,5

Після того як ми знайшли значення змінної «х», то можемо знайти довжини сторін «АВ» та «ВС». Просто підставимо у вирази «АВ» та «ВС» замість «х» число «7,5».

АВ = 30 - 7,5 = 22,5

ВС = 7,5

Найменшою стороною є «ВС» з довжиною «7,5».

Відповідь: 7,5.

Задача 6: Сторони трикутника дорівнюють «4» см, «5» см і «6» см. Знайти з точністю до «0,01» см довжину медіани проведеної до сторони завдовжки «5» см.

Візьмемо сторони трикутника «a», «b», «c»; де «a = 4», «b = 5», «c = 6». Отже, медіана буде проведена до сторони «b» позначимо її «m_b». Маючи три сторони трикутника ми можемо знайти медіану:

m_b = /1/2 2a² + 2c² - b²

Підставимо наші дані та отримаємо:

m_b = /1/22∙4² + 2∙6² - 5²

m_b = /1/2 ∙ √79

m_b = 4,44

Відповідь: 4,44.

Задача 7: Один з катетів і гіпотенуза прямокутного трикутника відповідно дорівнюють «5» см і «13» см. Знайти площу трикутника.

Площу прямокутного трикутника можемо знайти за формулою:

S = /ab/2

Де «a», «b» - катети прямокутного трикутника.

Оскільки, нам відомий лише один катет «а = 5», то необхідно знайти ще другий катет «b». Враховуючи, що гіпотенуза «c» нам відома «с = 13», то ми можемо знайти другий катет за теоремою Піфагора.

c² = a² + b²

b² = c² - a²

b = ±c² - a²

Підставимо наші дані та знайдемо другий катет. Оскільки довжина від’ємною бути не може, то від’ємний розв’язок відразу відкидаємо:

b = 13² - 5²

b = 12

Тепер у нас є всі дані для знаходження площі. Підставимо у формулу:

S = /5 ∙ 12/2

S = 30

Відповідь: 30.

Задача 8: Катети прямокутного трикутника дорівнюють «5» см і «12» см. Знайти радіус кола, вписаного в трикутник.

Оскільки, коло є вписаним у трикутник, то позначимо його радіус як «r». Позначимо катети як «a» та «b», а гіпотенузу «с»; де «a = 5», «b = 12», «с = ?».

Врахувавши, що коло є вписаним у коло, то його радіус можна знайти з формули знаходження площі трикутника:

S = pr

Де «р» - півпериметр трикутника в який вписане коло.

Площу прямокутного трикутника можна знайти за формулою:

S = /ab/2

Де «a», «b» - катети прямокутного трикутника.

Підставимо данні та знайдемо площу трикутника:

S = /5 ∙ 12/2

S = 30

Периметр трикутника можемо знайти як суму всіх його сторін поділену на два.

p = /a + b + c/2

Виходить, що нам не відома лише гіпотенуза трикутника. Знайдемо її за теоремою Піфагора.

c² = a² + b²

c = ±a² + b²

Оскільки довжина не може бути від’ємною, то ми відкинемо відразу розв’язок зі знаком «-». Підставимо наші значення та отримаємо:

c = 5² + 12²

c = 13

Тепер ми маємо всі данні для знаходження півпериметра трикутника. Отримаємо:

p = /5 + 12 + 13/2

p = 15

Ми маємо все для знаходження радіуса вписаного кола:

r = /S/p

r = /30/15

r = 2

Відповідь: 2.

Задача 9: Катет прямокутного трикутника дорівнює «28» см, різниця двох інших його сторін дорівнює «8» см. Знайти у сантиметрах гіпотенузу.

Позначимо перший катет як «а», другий катет як «b», гіпотенузу «с». За умовою задачі один з катетів рівний «28». Припустимо, що це є перший катет. Тобто: «a = 28». Вказано, що різниця двох інших сторін є «8». Оскільки у нас залишилися гіпотенуза та катет, то ми маємо віднімати від гіпотенузи катет. Це пов’язано з тим, що різниця є додатною, тобто ми від більшого числа віднімаємо менше. А гіпотенуза є найбільшою стороною прямокутного трикутника. Тому будемо мати: «c – b = 8». Якщо взяти, що катет «b» буде рівний «х», то будемо мати: «b = х». Тоді гіпотенуза «с» буде: «с – х = 8», звідси «с = х + 8».

Наші не відомі сторони є переписані через одну змінну «х». Щоб знайти її скористаємося теоремою Піфагора.

c² = a² + b²

Підставимо наші данні та розв’яжемо отримане рівняння:

(x + 8)² = 28² + x²

x² + 16x + 64 = 784 + x²

16x = 720

x = 45

Після того як знайшли значення змінної «х», то ми можемо знайти довжину гіпотенузи підставивши «45» замість «х». Отримаємо:

c = 45 + 8

c = 53

Відповідь: 53.

Задача 10: Проекції катетів прямокутного трикутника на гіпотенузу дорівнюють «4» см і «21» см. Знайти у сантиметрах менший катет.

Намалюємо прямокутний трикутник «АВС» з прямим кутом «В» та гіпотенузою «АС». Проведемо висоту «ВН».

Візьмемо, що проекція «АН» катета «АВ» буде рівна «4», «АН = 4»; проекція «СН» катета «ВС» буде рівна «21», «СН = 21». Оскільки відрізок «АН» є меншим за «СН», бо «4 < 21», то катет «АВ» є меншим за «ВС». Це означає, що нам необхідно знайти сторону «АВ».

Враховуючи, що ми маємо проекцію «АН» катета «АВ» на гіпотенузу «АС», то можемо скористатися співвідношеннями у прямокутному трикутнику. Отримаємо:

AB² = AH ∙ AC

AB = ± AH ∙ AC

Оскільки довжина від’ємною бути не може, то залишаємо лише додатний розв’язок:

AB = AH ∙ AC

Нам не відома гіпотенуза «АС». Оскільки, відрізок «АС» складається з відрізків «АН» та «СН», то виходить, що довжина «АС» буде рівна сумі довжин «АН» та «СН».

АС = АН + СН

Підставимо значення та отримаємо:

АС = 4 + 21

АС = 25

Тепер у нас є всі данні для знаходження катета «АВ». Підставимо та отримаємо:

АВ = 4 ∙ 25

АВ = 10

Відповідь: 10.

Задача 11: Периметр рівнобедреного трикутника дорівнює «20». Знайти його основу, якщо вона на «2» більша від бічної сторони.

Намалюємо рівнобедрений трикутник «АВС», де «АВ» та «ВС» - бічні сторони, «АС» - основа трикутника.

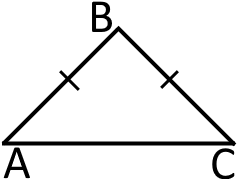
Позначимо довжину сторін «АВ» та «ВС» через «х». Тоді основа «АС» буде мати довжину «х + 2».

Після того як ми переписали всі сторони через одну змінну «х» ми можемо її знайти записавши рівняння периметру:

АВ + ВС + АС = Р

х + х + х + 2 = 20

3х = 20 - 2

3х = 18

х = 18 ∶ 3

х = 6

Підставимо «6» замість «х» та знайдемо основу трикутника:

АС = 6 + 2

АС = 8

Відповідь: 8.