Метод інтервалів
Одним з найпопулярніших методів розв’язувати нерівність є метод інтервалів. За його допомогою можна розв’язати нерівність. Хоча його реальна ефективність помітна лише в певних ситуаціях.
Розглянемо загальний принцип методу інтервалів:
1. Дуже часто в першу чергу визначають область допустимих значень Звісно, це можна робити трішки пізніше. Зауважимо, що в більшості випадках коли доводиться шукати ОДЗ метод інтервалів це буде не найкращим вибором (наприклад у нерівностях з коренем).
2. Наступним кроком є заміна знаку нерівності на знак рівності
3. Далі варто розв’язати отримане рівняння. Для того щоб метод інтервалів був ефективним намагаються отримане рівняння розкладати на максимально прості множники (тобто, щоб змінна не була у степені) та прирівнювати його до нуля. Тобто, зводити до вигляду: або На цьому ж етапі дуже зручно шукати ОДЗ. В реальності не заміняти знак нерівності на знак рівності але розкласти на прості множники буде необхідно.
4. Отримані розв’язки наносять на числову пряму. Не забуваємо, що точки можуть бути (не виколотими) або (виколотими). Детальніше про це читайте тут. Після чого, ми отримаємо проміжки, які називають інтервалами.
5. Далі ми обираємо довільне число в межах кожного інтервалу та підставляємо його у рівняння або нерівність (в ті де ми розклали на прості множники). Коли ми підставимо число, то зможемо визначити знак цього виразу. Нам не знаходити конкретне число після підстановки. Достатньо знайти лише його знак.
6. Обираємо проміжки зі знаком який нам підходить по нерівності. Якщо ми маємо нерівності то нам потрібен знак а якщо нерівності то знак
7. Записуємо відповідь.
Для даного методу вам варто розуміти як виносити спільний множник за дужки, метод групування, потрібно знати формули скороченого множення і як розкладати квадратний тричлен на множники.
Розглянемо метод інтервалів на реальних прикладах.
Розв’язати нерівність:
Цей приклад є ідеальним для того щоб використати метод інтервалів. Ми маємо множення декількох дужок і порівнюємо з нулем. В прикладі не має коренів, модулів і подібних речей. Всі дужки та змінні є в першому степені.
Отже, нам варто прирівняти до нуля даний вираз та розв’язати отримане рівняння.
(x-3)(2x+4)(1-x) = 0
Пам’ятаємо, якщо у нас є множення декількох дужок (виразів) і в результаті ми отримуємо нуль, то це означає, що одна із дужок (виразів) є нулем.
або або
або або
Наносимо отримані розв’язки на числову пряму. Враховуючи, що нерівність у нас є не суворою, то точки будуть зафарбовані (не виколоті).
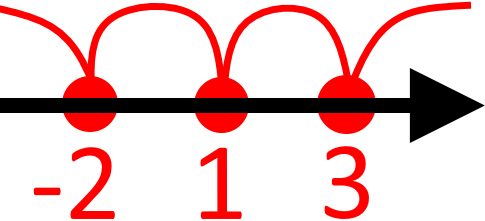
Тепер нам необхідно підставити з кожного проміжку якесь числа та знайти знак виразу.
Візьмемо для прикладу з проміжку число Пам’ятаємо, що нам достатньо знати лише знак результату. Тому, знайдемо знак кожної дужки, а потім знак цілого виразу.
x - 3:
2x + 4:
1 - x:
Отже, на проміжку ми будемо мати такий знак виразу:
+ ∙ + ∙ - = -
Тобто:
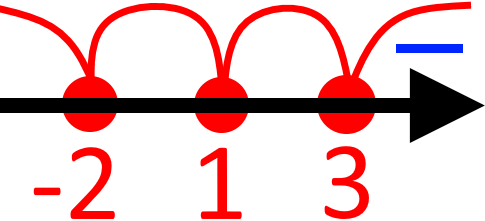
Тепер головний момент за який люблять метод інтервалів. Якщо, ви маєте множення/ділення ПРОСТИХ виразів, тобто, виразів у яких не має степеня, кореня, модуля і так далі, то знаки інтервалів будуть чергуватися.
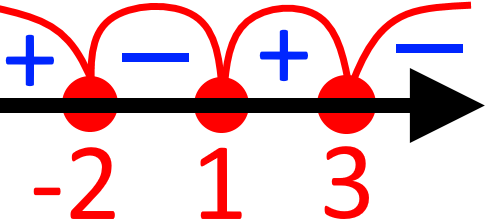
В цьому ви можете переконатися підставляючи числа з кожного інтервалу у рівняння/нерівність.
Після чого, залишається обрати лише проміжок (проміжки) які нам підходять. Враховуючи, що вираз є за нуль, то нам необхідні проміжки зі знаком
x ∈(-∞; -2] ∪ [1; 3]
Якщо дужки (вираз) є у парному степені, під модулем або під коренем парного степеня, то чергування знаків буде відбуватися за новими правилами.
В такій ситуації знаки біля розв’язку, що є у парному степені (і так далі) будуть однаковими, а решта продовжать чергуватися.
Наприклад:
Спробуємо розкласти на прості множники наші вирази.
У чисельнику ми маємо квадратний тричлен Розкласти квадратний тричлен можна за правилом де квадратного рівняння.
Розв’язками квадратного рівняння будуть а коефіцієнт в нас є тому ми зможемо розкласти наший тричлен так:
(x + 4)(x - 5)
У знаменнику ми маємо формулу скороченого множення
Тепер наший вираз виглядатиме так:
(x + 4)(x - 5)(x - 2)2 ≥ 0
Прирівняємо нерівність до нуля та знайдемо розв’язки рівняння.
(x + 4)(x - 5)(x - 2)2 = 0
Ми отримали дробово-раціональне рівняння Детальніше про них ви можете прочитати тут.
Нам необхідно прирівняти чисельник до нуля:
(x + 4)(x - 5) = 0
або
або
А знаменник не рівний нулеві:
(x - 2)2 ≠ 0
x - 2 ≠ 0
x ≠ 2
Нанесемо отримані розв’язки і не розв’язки на координатну пряму. Враховуючи, що ми маємо нерівність більшу-рівну за нуль. То, при цьому розв’язки ми позначатимемо зафарбованими (не виколоті) точками, а не розв’язки не зафарбованими (виколоті).

Підставлятимемо числа з кожного проміжку (інтервалу) та знайдемо знаки виразу на них.
Розглянемо проміжок Підставимо для прикладу число
x + 4:
x - 5:
x - 2:
Отже, на проміжку ми будемо мати такий знак виразу:
/+ ∙ +/+ = +
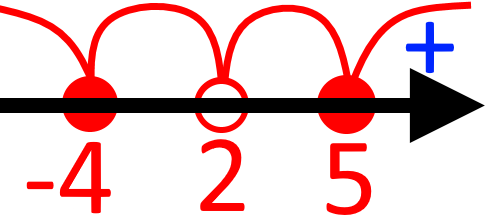
Якби ми чергували знаки, то отримали б такі знаки проміжків:
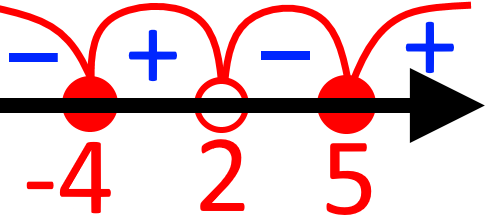
Але через те, що ми маємо вираз який є постійно додатним (бо число у парному степені завжди буде додатним), то знаки біля числа (в сусідніх інтервалах) будуть дублюватися. І реальні знаки інтервалів будуть такими:
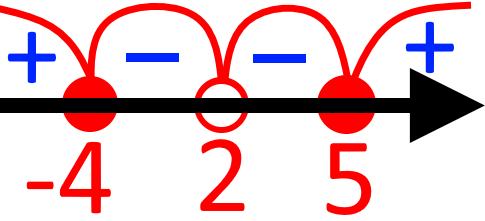
Такі числа намагаються якось позначати. Наприклад, їх можна обводити на координатній прямій. Такі позначення є виключно для вас. Тому, можете придумати свій особистий
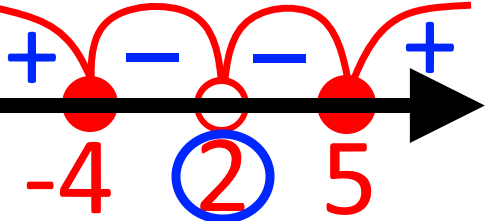
Після чого залишається обрати проміжки з підходящим знаком:
x ∈ (-∞; -4] ∪ [5; +∞)