Ірраціональні рівняння
Поняття ірраціонального рівняння
Рівняння називають ірраціональним, якщо воно містить невідомі під знаком кореня.
Розглянемо деякі види ірраціональних рівнянь та методи їх розв’язання.
Відразу зауважимо, що для всіх варіантів розглядаємо - натуральне число. функції зі змінною Також для простоти розглядатимемо схеми розв’язання у вигляді таблиці.
Рівняння вигляду: де
| n/f(x) = a | ||
| n - парне | n - непарне | |
| a ≥ 0 | a < 0 | f(x) = an |
| { | Рівняння розв’язків не має | |
Приклад:
Оскільки є корінь квадратний (тобто то це означає, що (корінь парного степеня завжди є більшим або рівним нулю). А в нашому випадку корінь є рівний від’ємному числу (числу яке є меншим за нуль). Звідси слідує, що рівняння не має коренів.
Приклад:
Оскільки є корінь квадратний (тобто то це означає, що (корінь парного степеня завжди є більшим або рівним нулю). А в нашому випадку корінь є рівний додатному числу (числу яке є більшим за нуль). Звідси слідує, що рівняння має корені.
Отже, необхідно підняти ліву та праву частину до квадрату (тому, що корінь квадратний).
Розв’язок можна записати у вигляді системи:
Перший вираз у системі є нерівністю. Вона необхідна для того щоб виключити можливі зайві розв’язки. Оскільки при розв’язанні рівняння може вийти корінь (розв’язок) при якому підкореневий вираз стане меншим нуля.
Приклад:
3/x - 3 = -3
Оскільки є корінь кубічний то це означає, що рівність матиме розв’язки не залежно від правої частини (не має значення додатній чи від’ємний вираз стоїть справа). Отже просто піднімаємо ліву та праву частину до третього степеня.
(3/x - 3)3 = (-3)3
x - 3 = -27
x = -27 + 3
x = -24
Рівняння вигляду:
| n/f(x) = g(x) | ||
| n - парне | n - непарне | |
| {f(x) = [g(x)]ng(x) ≥ 0f(x) ≥ 0 | f(x) = [g(x)]n | |
Приклад:
x + 5 = x - 1
Оскільки є корінь квадратний (тобто то це означає, що (корінь парного степеня завжди є більшим або рівним нулю). Звідси слідує, що підкореневий вираз права частина рівняння та має бути має бути більшою або рівною нулеві, тобто , . Якщо корінь є не парного степеня, то ці умови є не обов’язковими.
{x + 5 ≥ 0x - 1 ≥ 0(x + 5)2 = (x - 1)2
{x ≥ -5x ≥ 1(x + 5)2 = (x - 1)2
З та знаходимо, що Обираємо спільне для обох нерівностей. Детальніше можете прочитати тут. Це необхідно зробити щоб перевірити знайдені розв’язки. В такий спосіб шукаємо область визначення. Область визначення – це множина всіх дійсних значень при яких водночас мають зміст вирази, що входять до рівняння.
Тепер необхідно розв’язати рівняння, та знайти
(x + 5)2 = (x - 1)2
Піднявши ліву та праву частину рівняння до квадрату отримаємо:
x + 5 = x2 - 2x + 1
Скористаємося тим, що помінявши частини рівняння місцями нічого не зміниться (тобто, якщо написати повністю праву частину рівняння ліворуч, а ліву праворуч, то отримаємо таке ж саме рівняння).
x2 - 2x + 1 = x + 5
Переносимо все в ліву частину (варто не забувати, що при перенесені з однієї частини в іншу знаки та змінюються на протилежні. В попередньому кроці ми не змінювали знаки оскільки повністю переносили частини рівняння). Отримаємо:
x2 - 2x + 1 - x - 5 = 0
Виконавши дії додавання та віднімання (пам’ятаємо, що числа з додаються лише до чисел з з до та до чисел
x2 - 3x - 4 = 0
Це є квадратне рівняння. Детальніше як його розв’язувати можна прочитати тут. А зараз будуть виконані головні кроки:
D = b2 - 4ac
x1,2 = /-b ± √D/2a
x1 = /-(-3) + √25/2·1 = 4
x2 = /-(-3) - √25/2·1 = -1
Оскільки не задовольняє умову то це не є коренем (розв’язком) рівняння. Отже, відповідь: корінь (розв’язок) рівняння.
Рівняння вигляду:
| n/f(x) = n/g(x) | ||
| n - парне | n - непарне | |
| {/f(x) = g(x)/f(x) ≥ 0/g(x) ≥ 0 | f(x) = g(x) | |
Приклад:
x2 + 3x = 4x + 2
Оскільки показник кореня є парне число, то таке рівняння розв’язується системою. Напишемо її, для зручності взявши праву частину більшою або рівною нулеві (оскільки там лінійне рівняння). Отримаємо:
{ x2 + 3x = 4x + 24x + 2 ≥ 0x2 + 3x ≥ 0
Піднімемо в рівнянні обидві частини до квадрату (оскільки показник кореня є А у нерівності виразимо «х».
{( x2 + 3x )2 = (4x + 2)2x ≥ x ≥ 0; x ≥ -3
З та будемо мати, що Детальніше можете прочитати тут.
{x2 + 3x = 4x + 2x ≥ 0
{x2 + 3x - 4x - 2 = 0x ≥ 0
{x2 - x - 2 = 0x ≥ 0
Отримали квадратне рівняння. Розв’яжемо його.
x2 - x - 2 = 0
D = (-1)2 - 4 · 1 · (-2) = 9
x1 = /-(-1) + √9/2 · 1 = 2
x2 = /-(-1) - √9/2 · 1 = -1
Врахувавши умову отримаємо, що не є коренем (розв’язком) рівняння. Тому коренем (розв’язком) рівняння є лише
Ірраціональні рівняння, що містять декілька квадратних коренів. Рівняння вигляду: та подібні.
Такі рівняння варто розпочинати з визначення ОДЗ. Після чого можна скористатися одним із двох запропонованих способів.
Перший спосіб
Забезпечуємо невід’ємність лівої та правої частини рівняння. Тобто, якщо є (число або вираз) зі знаком мінус то переносимо його (їх) у протилежну частину при цьому змінюємо знаки на протилежні. Якщо говорити простими словами, то головна мета це позбутися віднімання. Наступний крок це підняття до квадрату лівої та правої чистини рівняння. Далі необхідно отримане рівняння спростити (додати або відняти відомі до відомих, невідомі до невідомих, розкрити дужки і тощо). Після спрощень отримаємо один із розглянутих типів рівнянь.
Приклад:
x + 1 - x - 2 = 1
Знайдемо область допустимих значень (ОДЗ). Для цього необхідно підкореневі вирази записати щоб вони були більші або рівні нулеві. Це зручно робити системою:
{/x + 1 ≥ 0/x - 2 ≥ 0
{/x ≥ -1/x ≥ 2
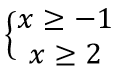
Звідси отримаємо, що має бути більшим або рівним двом (оскільки цей проміжок є спільний для обох нерівностей).
Позбудемося від’ємності в рівнянні. Для цього перенесемо радикал в праву частину (це необхідно щоб зник знак Отримаємо таке рівняння:
x + 1 = 1 + x - 2
Тепер ліва та права частина рівняння є невід’ємними. Піднесемо їх до квадрату:
(x + 1)2 = (1 + x - 2)2
x + 1 = 1 + 2x - 2 + x - 2
Поміняємо частини рівняння місцями (зробимо це для зручності) та виконаємо дії в лівій частині
1 + 2x - 2 + x - 2 = x + 1
2x - 2 + x - 1 = x + 1
Перенесемо невідомі (числа з ліворуч, а відомі (числа праворуч при цьому змінивши знаки на протилежні.
2x - 2 + x - x = 1 + 1
2x - 2 = 2
Поділимо обидві частини рівняння на
x - 2 = 1
Отримали вигляд рівняння Розв’яжемо відповідним методом. Піднімемо обидві частини до квадрату.
(x - 2)2 = 12
x - 2 = 1
x = 3
Значення входить у ОДЗ, тому є коренем рівняння.
Другий спосіб
Цей спосіб полягає у тому, що ліву та праву частину рівняння відразу піднімають до квадрату (без забезпечення невід’ємності). Але такий спосіб має декілька недоліків. Він може призвести до появи сторонніх розв’язків. В такому випадку можна запропонувати два підходи: Перший підхід полягає в тому, що необхідно підставляти отримані корені у початкове рівняння для перевірки. Але якщо отримані корені є ірраціональними числами, то така перевірка доставить багато проблем. Другий підхід полягає у переході до системи, яка є рівносильною даному рівнянню. Таку систему можна отримати, якщо доповнити рівняння, в якому записані ліва та права частини, піднесені до квадрата, нерівністю, що забезпечує однаковий знак лівої та правої частин.
Приклад:
x + 3 + x + 8 = 5
Знайдемо ОДЗ рівняння. Для цього необхідно підкореневі вирази зробити більшими або рівними нулеві. Напишемо це у вигляді системи:
{/x + 3 ≥ 0/x + 8 ≥ 0
{/x ≥ -3/x ≥ -8
Звідси отримаємо, що
Ліва та права частина рівняння є невід’ємною, тому їх можна підносити до квадрату (тому, що показник кореня двійка). Якщо розв’язувати так, то отримаємо доволі складне рівняння. Це зумовлено тим, що не скорочується після зникання кореня.
(x + 3 + x + 8)2 = 52
x + 3 + 2x + 3x + 8 + x + 8 = 25
2x + 11 + 2x + 3x + 8 = 25
Саме тому таке рівняння буде доволі складно розв’язувати. Звісно, якщо «х» зникне, то рівняння перетвориться на одне з тих, що розглядалися вище і розв’язати його буде не так складно. Таке рівняння можна також розв’язати. Для цього необхідно перенести все, що не корінь в іншу частину (розділити радикали від не радикалів) після чого підняти обидві частини до квадрату (або іншого степеня, в залежності від показника кореня).
2x + 3x + 8 = 25 - 11 - 2x
2x + 3x + 8 = 14 - 2x
x + 3x + 8 = 7 - x
(x + 3x + 8)2 = (7 - x)2
Після чого необхідно знайти корені отриманого рівняння та перевірити чи входять вони у ОДЗ та підставити у початкове рівняння для перевірки (щоб остаточно переконатися у правильності розв’язку).
25x - 25 = 0
25x = 25
x = 1
входить у ОДЗ але варто виконати перевірку підставивши це значення у початкове рівняння.
x + 3 + x + 8 = 5
1 + 3 + 1 + 8 = 5
4 + 9 = 5
2 + 3 = 5
5 = 5
Отже - єдиний корінь рівняння.
Але можна скористатися іншим варіантом. Перенесемо один із радикалів в іншу частину. Після піднесемо обидві частини до необхідного степеня.
x + 3 = 5 - x + 8
(x + 3)2 = (5 - x + 8)2
x + 3 = 25 - 2·5·x + 8 + x + 8
x + 3 = 33 - 10x + 8 + x
Перенесемо радикал у ліву частину рівняння (щоб він був зі знаком а все інше у праву змінивши при цьому знаки на протилежні.
10x + 8 = 33 + x - x - 3
10x + 8 = 30
Розділимо обидві частини рівняння на
x + 8 = 3
Отримали ірраціональне рівняння яке було розглянуто раніше
Піднімемо обидві частини до квадрату та знайдемо корінь рівняння.
(x + 8)2 = 32
x + 8 = 9
x = 1
«х=1» входить у ОДЗ але варто виконати перевірку підставивши це значення у початкове рівняння.
x + 3 + x + 8 = 5
1 + 3 + 1 + 8 = 5
4 + 9 = 5
2 + 3 = 5
5 = 5
Отже - єдиний корінь рівняння.
Як видно в обох варіантах отримали однаковий розв’язок. Яким користуватися обирати вам але не забувайте виконувати перевірку! Краще витратити лишні декілька хвилин чим не помітити помилку.
Приклад:
5x + 5 + 2x + 1 = 3x + 4
Знайдемо ОДЗ. Напишемо це у вигляді системи нерівностей:
{/5x + 5 ≥ 0/2x + 1 ≥ 0/3x + 4 ≥ 0
{x ≥ -1x ≥ -x ≥ -
З відси отримаємо, що
Оскільки обидві частини рівняння є невід’ємними, то можна скористатися двома варіантами, що розглядали раніше. Тобто можна піднімати до степеня відразу ліву та праву частину або можна один радикал з лівої частини перенести в праву і після цього підняти степеня. Розглянемо обидва варіанти.
Розглянемо перший варіант. Піднімемо обидві частини одночасно:
(5x + 5 + 2x + 1)2 = (3x + 4)2
5x + 5 + 25x + 52x + 1 + 2x + 1 = 3x + 4
25x + 52x + 1 = -4x - 2
5x + 52x + 1 = -(2x - 1)
(5x + 52x + 1)2 = (-(2x - 1))2
(5x + 5)(2x + 1) = (-1)2(2x - 1)2
10x2 + 15x + 5 = 4x2 + 4x + 1
10x2 + 15x + 5 - 4x2 - 4x - 1 = 0
6x2 + 11x + 4 = 0
Отже отримали квадратне рівняння. Розв’яжемо його.
D = (11)2 - 4 · 4 · 6 = 121 - 96 = 25
x1 = /-11 + √25/2 · 6 = /-11 + 5/12 = -/1/2 = -0,5;
x2 = /-11 - √25/2 · 6 = /-11 - 5/12 = -/4/3;
Під ОДЗ підходить лише Підставимо цей розв’язок у початкове рівняння для перевірки.
5 · (-0,5) + 5 + 2 · (-0,5) + 1 = 3 · (-0,5) + 4
√2,5 + √0 = √2,5
√2,5 = √2,5
Ліва та права частини рівняння однакові. Отже є розв’язком початкового рівняння.
Спробуємо розв'язати рівняння другим способом. Для цього перенесемо радикал у праву частину рівняння (не забуваємо при цьому змінити його знак на протилежний).
5x + 5 = 3x + 4 - 2x + 1
Тепер є два варіанти розв’язання цього рівняння.
Перший, подібний до того, що вже робили. Тобто підняти обидві частини рівняння до квадрату. Відділити корінь від решти і знову підняти до квадрату. Після чого знайти зміну. Оскільки цей спосіб надзвичайно подібний до того, що вже зробили, то його розглядати не будемо.
Але розглянемо інший варіант. Оскільки ліва частина невід’ємна, тому невід’ємною має бути і права частина. Отже, рівняння рівносильне системі:
{ 5x + 5 = 3x + 4 - 2x + 1 3x + 4 - 2x + 1 ≥ 0 5x + 5 ≥ 0
{ (5x + 5)2 = (3x + 4 - 2x + 1)2 (3x + 4)2 ≥ (2x + 1)2 (5x + 5)2 ≥ 0
{ 5x + 5 = 3x + 4 - 23x + 42x + 1 + 2x + 1 3x + 4 ≥ 2x + 1 5x + 5 ≥ 0
{ 23x + 42x + 1 = 3x + 4 - 5x - 5 + 2x + 1 3x - 2x ≥ 1 - 4 5x ≥ -5
{ 23x + 42x + 1 = 0 x ≥ -3 x ≥ -1
Отримали, що та Отже, будемо мати Тепер розв'яжемо рівняння Розділимо його на два рівняння та
{ [/3x + 4 = 0/2x + 1 = 0 x ≥ -1
{ [x = - 4/3x = - 1/2 x ≥ -1
Отже отримавши два розв’язки і перевіривши їх з ОДЗ бачимо, що лише задовольняє умову Відповідно є лише один розв’язок цього рівняння.
Заміна змінних у ірраціональному рівнянні
Деякі ірраціональні рівняння зручно розв’язувати, використовуючи заміну змінної При цьому необхідно пам’ятати, що при нова змінна має задовольняти умову
Приклад:
83 - x - 3 - x = 2
Як помітно в рівнянні є для простоти розв’язання можна цей радикал замінити на нову змінну Використовуючи спосіб заміни варто пам’ятати, що стара змінна має повністю зникнути після заміни. Також у випадку парного показника кореня варто дотримуватися того, що нова змінна має бути більшою або рівною за нуль. В нашому випадку лише більшою оскільки радикал знаходиться в знаменнику, отже
/8/t - t = 2
Зведемо ліву частину до спільного знаменника:
8 - t2t = 2
Помножимо навхрест (спосіб метелика) ліву та праву частину:
8 - t2 = 2t
Перенесемо все в одну частину (в ліву та помножимо на або в праву та поміняємо частини місцями), при цьому не забуваємо, що при перенесенні знаки змінюються на протилежні:
t2 + 2t - 8 = 0
Отже отримали квадратне рівняння. Як такі рівняння розв’язувати можна ознайомитися тут. Ми ж просто напишемо корені цього рівняння:
t1 = 2; t2 = -4
Враховуючи, що маємо лише один розв’язок Тепер необхідно повернутися до заміни.
3 - x = 2
Після повернення до заміни отримали вигляд рівняння яке розглядалося раніше.
(3 - x)2 = 22
3 - x = 4
x = -1