Квадратні нерівності
Нерівність виду «ax2 + bx + c > 0» (або «ax2 + bx + c < 0»), де «a», «b», «c» - деякі числа, «a ≠ 0» і «x» - змінна, називається квадратною. Така нерівність може бути як суворою («>» або «< ») так і не суворою («≥» або «≤»).
Приклади: ; ,оскільки
Для розв’язування квадратних нерівностей використовують ескіз графіка функції , тобто параболу.
Розв’язування будь-якої квадратичної нерівності можна звести до одного з шести випадків. Розглянемо це у вигляді таблиці.
| D < 0 | D = 0 | D > 0 | |
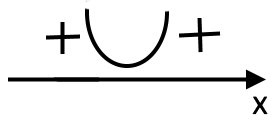 «х» - будь яке число; розв'язків немає; |
 ; розв'язків немає; |
 x ∈ (x1; x2) |
|
 |
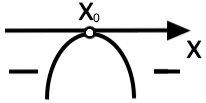 |
 |
Розв’язками нерівності
Розв’язками нерівності
Алгоритм розв’язування квадратних нерівностей:
Визначаємо напрямок віток параболи, яка є графіком функції
Знаходимо корені квадратного тричлена
Будуємо ескіз графіка функції
Вибираємо значення змінної, які відповідають розв’язкам нерівності
Записати відповідь
Приклад:
-x2 + 4x - 3 ≤ 0
1. Коефіцієнт «а» рівний «-1», отже парабола буде вітками до низу (дивитися табличку. Якщо «а» більше за нуль, то парабола вітками до гори, якщо менше нуля, то вітками до низу).
2. Розв’яжемо рівняння
D = 42 - 4 · (-1) · (-3) = 16 - 12 = 4; D>0
x1 = /-4 + √4/-2= 1; x2 = /-4 - √4/-2 = 3
3. Тепер необхідно побудувати ескіз графіка нашої функції. Оскільки дискримінант більший за нуль, то парабола перетнеться з віссю «0х» у двох точках «х1 = 1» та «х2 = 3».
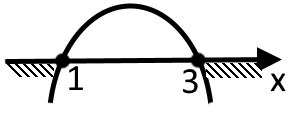
4. Оскільки нерівність має бути меншою або рівною за нуль, то її задовольняють всі значення змінної «х» які знаходяться не в зоні параболи (на малюнку виділено штриховкою) та точки перетину параболи з віссю «0х» (оскільки нерівність може бути рівна нулю).
x ∈ (-∞; 1] ∪ [3; +∞)
Відповідь: (-∞; 1]∪[3; ∞)