Все про коло
Коло, його елементи
Коло – геометрична фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Цю точку називають центром кола, а відрізок, що сполучає центр кола з будь-якою точкою кола, називають радіусом. Радіус позначають буквою «r».

Пряма яка сполучає дві точки кола і проходить через його центр, називається діаметром. Діаметр позначають буквою «d». Діаметр рівний двом радіусам А пряма яка сполучає дві точки кола і не проходить через його центр, називається хордою. Найбільша хорда – діаметр.
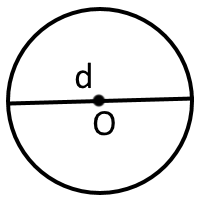
Діаметр кола, який проходить через середину хорди, перпендикулярний до неї.
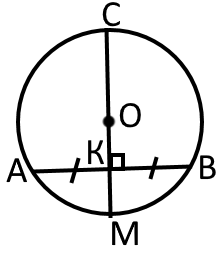
Діаметр кола, що проходить через середину хорди, яка не є іншим діаметром, перпендикулярний до неї.
«К» - точка перетину діаметра та хорди. Отже отримаємо, що: та
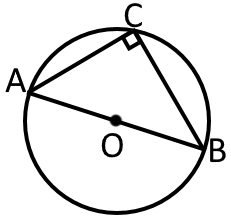
Діаметр з будь-якої точки кола видно під прямим кутом. Тобто, якщо взяти будь-яку точку кола і її з’єднати із кінцями діаметру, то утвориться прямий кут.
- довільна точка кола, і - відрізки, що сполучають точку з кінцями діаметра кола. Звідси слідує, що Це виникає через те, що діаметр ділить коло на дві однакові частини. Тобто на дві рівні дуги градусна міра яких є вписаним кутом (описано нижче) тому він буде рівний градусній мірі дуги розділеній на два
Круг та його елементи
Частина площини, обмежена колом, разом із самим колом, називають кругом. Центром, радіусом, діаметром, хордою, круга називають відповідно центр, радіус, діаметр, хорду кола, яка є межею даного круга. Тобто всі елементи які є у колі яке обмежує даний круг можна застосовувати і для круга. Наприклад: радіус кола рівний і радіус круга який є обмежений цим колом буде також
Центральні та вписані кути
Центральним називають кут вершина якого знаходиться у центрі кола (від чого і пішла його назва).

Як видно на малюнку - центральний кут. Він розбиває коло на дві дуги та (В житті ви часто з цим зустрічаєтеся. Наприклад коли у вас є торт, піца або ще щось круглої форми від якого ви відріжете шматочок. В такому випадку ви отримаєте один великий шматок і один шматок меншої форми, звісно ж за умови, що розріз буде проходити не по середині. В такому випадку буде два однакових шматочки). Величину дуги кола можна вимірювати в градусах. Градусною мірою дуги кола називають градусну міру відповідного центрального кута. Слово «дуга» можна замінити символом
Наприклад, якщо то А
Якщо з’єднати точки та то - буде хордою. А трикутник буде рівнобедреним, де
Кажуть, що спирається на дугу (на хорду
Вписаним називають кут, вершина якого належить колу, а сторони перетинають його. - вписаний кут.

Величина вписаного кута вимірюється половиною величини дуги, на яку він спирається. Також можна сказати, що вписаний кут буде рівний половині центрального кута, якщо вони спираються на одну і ту саму дугу.
- вписаний кут, що спирається на - центральний кут, що спирається на Тоді
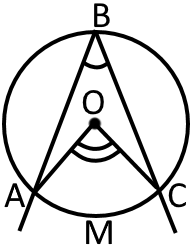
Також можна виділити декілька наслідків:
Вписані кути, що спираються на одну і ту саму дугу, рівні.
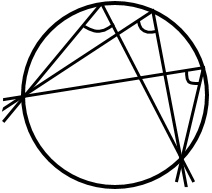
Вписаний кут, що спирається на діаметр, прямий.

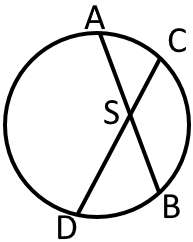
Властивість хорд, що перетинаються
Якщо хорди і перетинаються в точці то
Дотична до кола та її властивість
Дотичною до кола називають пряму, яка має єдину спільну точку з колом. Цю точку називають точкою дотику.
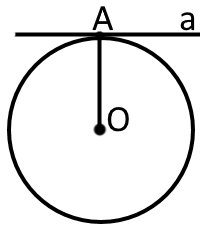
Для властивостей пряма - дотична до кола; точка - точка дотику; - центр кола; - радіус кола.
Властивості дотичної до кола:
1. Дотична до кола перпендикулярна до радіуса, проведеного у точку дотику.
2. Відстань від центра кола до дотичної до цього кола дорівнює радіусу кола. (Відстань від центру кола точки до дотичної «а» дорівнює радіусу кола
3. Відрізки дотичних, проведених з однієї точки до кола, рівні. (До кола із точки проведено дві дотичні; і - точки дотику. Тоді
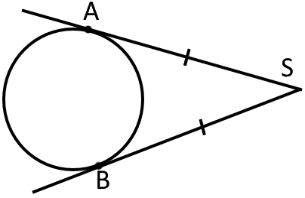
Січна – це пряма яка має з колом дві спільні точки.

Властивості дотичної та січної
1. Якщо з точки яка знаходиться поза колом, провести січну, яка перетинає коло в точках та та дотичну де - точка дотику, то:
«SC2 = SA · SB»

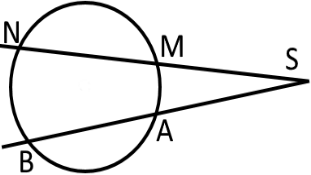
2. Якщо з точки провести дві січні, одна з яких перетинає коло в точках і а друга в точках «М» і , то:
«SA · SB = SM · SK»
Взаємне розміщення двох кіл
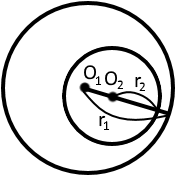
Розглянемо можливі випадки взаємного розміщення двох кіл, центри яких точки і а радіуси відповідно і де (кола можуть бути однаковими або різними).
1. Два кола не перетинаються, тобто не мають спільних точок. Тоді, коли, відстань між їх центрами є більшою за суму або меншою різницю їх радіусів:
«O1O2 > r1 + r2»

або «O1O2 < r1 - r2»
2. Два кола мають єдину спільну точку. В такому випадку кажуть, що кола дотикаються, а їх спільну точку називають точкою дотику.
Можливі два випадки розміщення таких кіл:
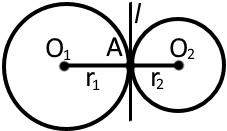
Перший: центри кіл розташовані по різні боки від точки дотику (справа та зліва від неї); такий дотик називається зовнішнім.
У такому випадку:
1) O1O2 = r1 + r2
2) У точці існує спільна дотична до двох кіл
3) l ⊥ O1O2
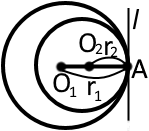
Другий: центри кіл розташовані по один бік від точки дотику (одне коло знаходиться в середині іншого); такий дотик називається внутрішнім.
У такому випадку:
1) O1O2 = r1 - r2
2) У точці існує спільна дотична до двох кіл
3) l ⊥ O1O2
3. Два кола мають дві спільні точки. Тоді коли (відстань між центрами є більшою за різницю та меншою за суму їх радіусів)

Довжина кола. Довжина дуги кола
Довжина кола, радіус якого дорівнює обчислюється за формулою:
C = 2πr
Довжина дуги що відповідає центральному куту кола радіусом обчислюється за формулою:
ln0 = πrn1800
