Для того щоб розв’язувати системи рівнянь варто ознайомитися з розділами: Система рівнянь; Квадратні рівняння; Рівняння, що зводяться до квадратних.

Найчастіше системи рівнянь розв’язують методом підстановки або графічним методом.

Користуючись методом виражання змінної варто пам’ятати, що краще за все виражати так щоб утворювався чим простіший вираз.

Для графічного методу варто розібратися із побудовою графіків функції.

1. Розв’язати систему: {/3x + 4y = 24/xy = 12

В даній системі яку б змінну і з якого б рівняння ми не виражали у нас буде утворюватися дріб. Але, якщо у першому рівнянні у знаменнику буде звичайне число, то у другому рівнянні в знаменнику буде змінна, що не зовсім зручно. Тому виразимо з першого рівняння наприклад змінну «х». Для цього нам необхідно «4у» перенести у протилежну сторону та поділити на «3» (бо біля «х» стоїть «3»). Отримаємо:

{/3x = 24 - 4y/xy = 12

{x = /24 - 4y/3xy = 12

Після того як виразили змінну «х» підставимо отриманий результат («/24 - 4y/3») в інше рівняння («xy = 12») замість вираженої змінної («х»). Отримаємо:

{x = /24 - 4y/3/24 - 4y/3 ∙ y = 12

Розв’яжемо рівняння, що утворилося після підстановки:

/24 - 4y/3 ∙ y = 12

/(24 - 4y)y/3 = 12

Помножимо весь вираз на «3» для того щоб позбутися знаменника.

/(24 - 4y)y/3 = 12 |∙3

(24 - 4y)y = 36

Знайдемо розв’язки даного рівняння. Для цього розкриємо дужки у лівій частині та перенесемо «36» з права на ліво:

24y - 4y² = 36

-4y² + 24y - 36 = 0

Для власної зручності поділимо весь вираз на «-4»:

-4y² + 24y - 36 = 0 |∶(-4)

y² - 6y + 9 = 0

D = (-6)² - 4∙1∙9 = 36 - 36 = 0

y = /-(-6)/2 ∙ 1 = 3

Ми знайшли значення однієї. Тепер варто знайти значення другої змінної («х»). Для цього нам необхідно підставити «3». Підставимо у друге рівняння:

x ∙ 3 = 12

x = /12/3

x = 4

Розв’язком початкової системи є пара чисел:

(4; 3)

Відповідь: (4; 3).

2. Розв’язати систему: {x² - xy - y² = 19x - y = 7

Виразимо з другого рівняння зміну «х» бо для цього достатньо лише перенести «-у» у протилежну сторону.

{x² - xy - y² = 19x = y + 7

Підставимо у перше рівняння замість «х» наший вираз «у + 7».

(y + 7)² - y(y + 7) - y² = 19

(y + 7)² - y(y + 7) - y² - 19 = 0

Розв’яжемо отримане рівняння:

y² + 14y + 49 - y² - 7y - y² - 19 = 0

-y² + 7y + 30 = 0

D = 7² - 4∙(-1)∙30 = 49 + 120 = 169

y₁ = /-7 + √169/2 ∙ (-1) = -3

y₂ = /-7 - √169/2 ∙ (-1) = 10

Отже, ми будемо мати два варіанти значення змінної «у». Залишається знайти значення змінної «х». Для цього варто підставити отримані значення замість «у» у будь-яке з початкових.

Підставлятимемо у друге рівняння.

При «у = -3», матимемо:

x = -3 + 7

x=4

Перша пара чисел яка є розв’язком початкової системи:

(4; -3)

При «у = 10», матимемо:

x = 10 + 7

x = 17

Друга пара чисел яка є розв’язком початкової системи:

(17; 10)

Відповідь: (4; -3); (17; 10).

3. Розв’язати систему: {4y - 3x = 45x² + 16y = 60

Часто не потрібно виражати повністю зміну щоб замість неї підставити вираз. Наприклад, якщо у другому рівнянні ми «16у» напишемо так «4 ∙ 4y», то з першого рівняння нам не обов’язково виражати «у» а достатньо «4у».

{4y = 3x + 45x² + 4 ∙ 4y = 60

Отже, підставимо «3х + 4» замість «4у» у друге рівняння:

{4y = 3x + 45x² + 4∙(3x + 4) = 60

Розв’яжемо отримане рівняння:

5x² + 4∙(3x + 4) = 60

5x² + 12x + 16 - 60 = 0

5x² + 12x - 44 = 0

D = 12² - 4∙5∙(-44) = 144 + 880 = 1024

x₁ = /-12 + √1024/2 ∙ 5 = 2

x₂ = /-12 - √1024/2 ∙ 5 = -4,4

Тепер варто знайти значення змінної «у». Для простоти будемо підставляти у перше рівняння.

При «х = 2» матимемо:

4y = 3 ∙ 2 + 4

4y = 10

y = /10/4

y = 2,5

Перша пара чисел яка є розв’язком початкової системи є такою:

(2; 2,5)

При «х = -4,4» матимемо:

4y = 3∙(-4,4) + 4

4y = -9,2

y = /-9,2/4

y = -2,3

Перша пара чисел яка є розв’язком початкової системи є такою:

(-4,4; -2,3)

Відповідь: (2; 2,5); (-4,4; -2,3).

4. Розв’язати систему: {/x/y + /6y/x = 5x² + 4xy - 3y² = 18

Як помітно виразити будь-яку зі змінних буде доволі таки складно. Також буде складно розв’язати графічним методом. В такому випадку часто використовують «змішаний» метод, а саме в першу чергу намагаються спростити систему методом додавання, після чого виражають одну зі змінних.

Для того щоб спростити наше рівняння під час додавання (коли, будемо використовувати метод додавання).

Зведемо ліву частину першого рівняння до одного єдиного дробу:

{x² + 6y²xy = 5x² + 4xy - 3y² = 18

В першому рівнянні скористаємося метеликом щоб позбутися дробу:

{x² + 6y²xy = /5/1x² + 4xy - 3y² = 18

{x² + 6y² = 5xyx² + 4xy - 3y² = 18

{x² - 5xy + 6y² = 0x² + 4xy - 3y² = 18

Тепер нам необхідно визначити який вираз будемо скорочувати. Наприклад, для того щоб скоротити «x²» необхідно або перше або друге рівняння помножити на «-1» (отримаємо однакові числа але з різними знаками біля «x²») після чого додати наші рівняння. Скорочення виразу «ху» нам нічого хорошого не дасть, бо залишаться «x²» та «y²» і виразити будь-яку змінну буде складно. Для того щоб скоротити «y²» варто помножити друге рівняння на «2» (отримаємо однакові числа але з різними знаками біля «y²») після чого необхідно додати наші рівняння.

Краще за все скоротити першим або третім способом, оскільки, тоді залишаться вираз «ху» з якого зручно виразити будь-яку зі змінних. Скоротимо вираз «y²» (скористаємося третім способом):

{x² - 5xy + 6y² = 0x² + 4xy - 3y² = 18 |∙2

{x² - 5xy + 6y² = 02x² + 8xy - 6y² = 36

Біля «y²» у нас однакові числа але з різними знаками, все чудово. Додаймо наші рівняння. Ліва частина до лівої, права до правої.

x²- 5xy + 6y² + 2x² + 8xy - 6y² = 36

3x² + 3xy = 36 |∶3

x² + xy = 12

Звідси ми можемо виразити змінну «у». Для цього варто винести за дужки «х» у лівій частинні рівняння.

x(x + y) = 12

Після чого розділимо на «х» обидві частини рівняння.

x + y = /12/x

Та перенесемо «х» з лівої частини у праву щоб виразити «у».

y = /12/x - x

Для своєї зручності можемо звести все до одного дробу.

y = 12 - x²x

Після того як ми виразили одну зі змінних нам необхідно підставити отриманий вираз у будь-яке початкове рівняння системи. Підставимо у друге.

x² + 4x ∙ 12 - x²x - 3 ∙ (12 - x²x)² = 18

Розв’яжемо отримане рівняння.

x² + 4x(12 - x²)x - 3(12 - x²)²x² = 18

Для того щоб позбутися знаменника ми можемо весь приклад помножити на «» але при цьому нам варто пам’ятати, що в такому випадку необхідно відкинути всі значення змінної «х» при яких знаменник перетвориться у нуль (бо на нуль ділити не можна), тому «х» не може бути рівний нулеві («x ≠ 0»).

x² + 4x(12 - x²)x - 3(12 - x²)²x² = 18 |∙x²

x⁴ + 4x(12 - x²) ∙ x - 3(12 - x²)² = 18x²

x⁴ + 4x²(12 - x²) - 3(12 - x²)² = 18x²

x⁴ + 48x² - 4x⁴ - 3(144 - 24x² + x⁴) - 18x² = 0

-3x⁴ + 30x² - 3(144 - 24x² + x⁴) = 0 |∶(-3)

x⁴ - 10x² + (144 - 24x² + x⁴) = 0

x⁴ + 144 - 24x² + x⁴ - 10x² = 0

2x⁴ - 34x² + 144 = 0 |∶2

x⁴ - 17x² + 72 = 0

Ми отримали біквадратне рівняння. Щоб його розв’язати варто скористатися заміною змінної:

x² = t

Після чого наше рівняння набуде такого вигляду:

t² - 17t + 72 = 0

D = (-17)² - 4∙1∙72 = 289 - 288 = 1

t₁ = /-(-17) + √1/2 ∙ 1 = 9

t₂ = /-(-17) - √1/2 ∙ 1 = 8

Ми розв’язали рівняння відносно змінної «t», тепер повернемося до змінної «х».

Отже, змінна «х» може набувати таких значень.

При «t = 9», матимемо:

x² = 9

x = ± √9

x = ±3

При «t = 8», матимемо:

x² = 8

x = ± √8

x = ± 2√2

Знайдемо тепер значення змінної «у» з виразу «y = /12/x - x».

При «х = 3», матимемо:

y = /12/3 - 3

y = 1

При «х = -3», матимемо:

y = /12/-3 - (-3)

y = -1

При «х = 2√2», матимемо:

y = /12/2√2 - 2√2

y = /6/√2 - 2√2

y = /6/√2 ∙ /√2/√2 - 2√2

y = /6√2/2 - 2√2

y = 3√2 - 2√2

y = √2

При «х = -2√2», матимемо:

y = /12/-2√2 - (-2√2)

y = /-6/√2 + 2√2

y = /-6/√2 ∙ /√2/√2 + 2√2

y = -/6√2/2 + 2√2

y = -3√2 + 2√2

y = -√2

Отже, розв’язками початкової системи будуть такі пари чисел:

(3; 1); (-3; -1); (2√2; √2); (-2√2; -√2)

Відповідь: (3; 1); (-3; -1); (2√2; √2); (-2√2; -√2)

5. Розв’язати систему: {3(x + y)² + 2(x - 2y)² = 52(x - 2y) - x - y = 1

Часто в складних системах використовують заміну змінних щоб спростити початкову систему.

Винесемо «-» у другому рівнянні з «- х – у» за дужки.

{3(x + y)² + 2(x - 2y)² = 52(x - 2y) - (x + y) = 1

Як помітно в обох рівняннях ми маємо вирази «х + у» та «х – 2у». Cкористаємося замінами:

{/x + y = u/x - 2y = v

Після чого наша система набуде такого вигляду:

{3u² + 2v² = 52v - u = 1

Як помітно завдяки заміні наша система набула простішого вигляду. Розв’яжемо її. Для цього виразимо «u» з другого рівняння.

{3u² + 2v² = 5-u = 1 - 2v |∙(-1)

{3u² + 2v² = 5u = 2v - 1

Та підставимо вираз «2v - 1» замість «u» у перше рівняння.

{3(2v - 1)² + 2v² = 5u = 2v - 1

Після чого розв’яжемо отримане рівняння:

3(2v - 1)² + 2v² = 5

3(4v² - 4v + 1) + 2v² - 5 = 0

12v² - 12v + 3 + 2v² - 5 = 0

14v² - 12v - 2 = 0 |∶2

7v² - 6v - 1 = 0

D = (-6)² - 4∙7∙(-1) = 36 + 28 = 64

v₁ = /-(-6) + √64/2 ∙ 7 = 1

v₂ = /-(-6) - √64/2 ∙ 7 = -/1/7

Знайдемо значення змінної «u».

При «v = 1», матимемо:

u = 2 ∙ 1 - 1

u = 1

Отже, перша пара чисел буде така:

u = 1; v = 1

При «v = -/1/7», матимемо:

u = 2 ∙ (-/1/7) - 1

u= -1/2/7

Отже, друга пара чисел буде така:

u = -1/2/7; v = -/1/7

Тепер варто розв’язати нашу систему:

{/x + y = u/x - 2y = v

При «u = 1; v = 1» будемо мати:

{/x + y = 1/x - 2y = 1

Виразимо змінну «х» з першого рівняння:

{/x = 1 - y/x - 2y = 1

Та підставимо у друге рівняння:

{/x = 1 - y/1 - y - 2y = 1

І розв’яжемо отримане рівняння:

1 - y - 2y = 1

-3y = 1 - 1

-3y = 0

y = 0

При «у = 0», матимемо:

x = 1 - 0

x = 1

Перша пара чисел:

(1; 0)

При «u = -1/2/7; v = -/1/7» будемо мати:

{x + y = -1/2/7x - 2y = -/1/7

Виразимо змінну «х» з першого рівняння:

{x = -1/2/7 - yx - 2y = -/1/7

Та підставимо у друге рівняння:

{x = -1/2/7 - y-1/2/7 - y - 2y = -/1/7

І розв’яжемо отримане рівняння:

-1/2/7 - y - 2y = -/1/7

-3y = 1/2/7 -/1/7

-3y = /9/7 -/1/7

-3y = /8/7 |∶(-3)

y = -/8/7 ∙ 3

y = -/8/21

При «у = -/8/21», матимемо:

x = -1/2/7 - (-/8/21)

x = -/9/7 + /8/21

x = /-9 · 3 + 8/21

x = -/19/21

Друга пара чисел:

(-/19/21; -/8/21)

Відповідь: (1; 0); (-/19/21; -/8/21).

6. Скільки розв’язків має система рівнянь: {y = (x - 5)²xy = 5

Для того щоб вирішити такі завдання часто використовують побудову ескізів (не точна побудова графіку, а лише його приблизний вигляд) графіків функції.

З ескізами графіків функції можна ознайомитися тут.

Поділимо у другому рівнянні на «х» для того щоб виразити змінну «у»:

{y = (x - 5)²xy = 5 |∶x

{y = (x - 5)²y = /5/x

Отже, ми будемо мати графік параболи у функції «y = (x - 5)²». При цьому вершину параболи ми можемо знайти за властивістю «y = f(x ± a)». Оскільки в стандартній функції параболи («y = x²») її вершина знаходиться у точці «(0; 0)», то у функції «y = (x - 5)²» вершина параболи зміститься у право на «5» і вершина буде знаходитися у точці «(5; 0)». Парабола буде вітками до гори, оскільки біля «x²» (якщо підняти дужки до квадрату) знаходиться «+».

Також будемо мати графік двох віток гіперболи з функції «y = /5/x». Оскільки, загальний вигляд цієї функції є таким: «y = /k/x». І при «k > 0» графік буде знаходитися у «І» та «ІІІ» чвертях, а при «k < 0» - у «ІІ» та «IV» чвертях. То у нашому випадку ми маємо графік буде розміщений у «І» та «ІІІ» чверті, бо «5 > 0». Також варто зауважити, що при «х = -5» матимемо «у = -1», а при «х = 5» буде «у = 1». Також «x ≠ 0», бо на нуль ділити не можна.

Побудуємо ескізи наших графіків. Ескіз функції «y = (x - 5)²» намалюємо червоним кольором, а «y = /5/x» - синім. Точки перетину позначимо зеленим.

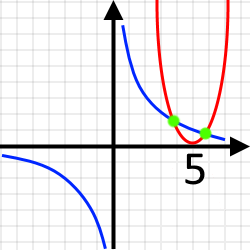
Як помітно у нас є дві точки перетину, тому система має два розв’язок.

Якщо необхідно знайти розв’язок системи, то розв’язком будуть координати точок перетину наших графіків.

Відповідь: система має два розв’язки.

7. Скільки розв’язків має система рівнянь: {x² + y² = 6xy = 1

Для того щоб знайти кількість розв’язків системи достатньо побудувати графіки функцій та знайти кількість точок перетину цих ескізів.

Виразимо з другого рівняння змінну «у».

{x² + y² = 6y = /1/x

Функція «x² + y² = 6» має графік кола. Загальний вигляд рівняння кола є таким: «(x - a)² + (y - b)² = R²»; де «(a; b)» - координати центру кола, «R» - радіус кола.

Оскільки, у нас не має жодних чисел біля «х» та «у», то центр кола буде знаходитися у точці «(0; 0)», а його радіус буде «R = √6».

Також будемо мати графік двох віток гіперболи з функції «y = /1/x». Оскільки, загальний вигляд цієї функції є таким: «y = /k/x». І при «k > 0» графік буде знаходитися у «І» та «ІІІ» чвертях, а при «k < 0» - у «ІІ» та «IV» чвертях. То у нашому випадку ми маємо графік буде розміщений у «І» та «ІІІ» чверті, бо «1 > 0». Також варто зауважити, що при «х = -1» матимемо «у = -1», а при «х = 1» буде «у = 1». Також «x ≠ 0», бо на нуль ділити не можна.

Побудуємо ескізи наших графіків. Ескіз функції «x² + y² = 6» намалюємо червоним кольором, а «y = /1/x» - синім. Точки перетину позначимо зеленим.

Як помітно ми маємо чотири точки перетину, тому система має чотири розв’язки. А розв’язками системи будуть координати точок перетину графіків функцій.

Відповідь: система має чотири розв’язки.

8. Розв’язати систему рівнянь: {/x + y = -2/y + z = -11/x + z = 1

Зверніть увагу! У нашій системі є три змінні та три рівняння. Систему можна розв’язати тоді, коли кількість рівнянь є більшою або такою ж як кількість змінних.

Системи в яких три та більше рівняння і змінних розв’язуються так же як і система з двома рівняннями та змінними. Єдине, якщо ви використовуєте метод виражання змінної, то варто все робити послідовно.

Наприклад: ми можемо виразити змінну «z» з третього рівняння та підставити результат у друге:

{/x + y = -2/y + z = -11/z = 1 - x

{/x + y = -2/y + 1 - x = -11/z = 1 - x

Тепер з другого рівняння ми можемо виразити змінну «у» та підставити у перше.

Порядок ви можете підлаштовувати під себе. В даному прикладі показаний лише принцип.

{/x + y = -2/y = x - 1 -11/z = 1 - x

{/x + y = -2/y = x - 12/z = 1 - x

{/x + x - 12 = -2/y = x - 12/z = 1 - x

Як помітно в першому рівнянні у нас залишилася лише одна єдина змінна «х». Розв’яжемо дане рівняння:

x + x - 12 = -2

2x = -2 + 12

2x = 10 |∶2

x = 5

Ми отримали значення змінної «х». Тепер варто у зворотному порядку знаходити решту змінних.

Ми знаходили змінну «х» підставляючи значення змінної «у», тому зараз варто знайти саме її (шукатимемо з другого рівняння, де вона вже є вираженою):

y = x - 12

При «х = 5», матимемо:

y = 5 - 12

y = -7

Тепер знайдемо змінну «z» (шукаємо з третього рівняння):

При «х = 5», матимемо:

z = 1 - x

z = 1 - 5

z = -4

Отже, розв’язком початкової системи буде така пара чисел (записуємо в такому порядку: (x; y; z)):

(5; -7; -4)

Відповідь: (5; -7; -4).