Для того, щоб успішно розв’язувати практичні завдання вам варто ознайомитися з теоретичним матеріалом як розв’язувати квадратні рівняння та квадратні нерівності.

1) Розв’язати нерівність: «x² - 4x < 0».

Для того, щоб розв’язати нерівність варто з першу знайти розв’язки рівняння. Замінимо знак нерівності «<» на рівність «=».

x² - 4x = 0

Це є неповне квадратне рівняння. Ми можемо його розв’язати за допомогою дискримінанту або методами неповних рівнянь. Оскільки, ми в усіх доданках маємо «x», то можна винести його як спільний множник за дужки:

x(x - 4) = 0

Маємо множення декількох виразів в результаті якого виходить нуль. Таке можливо лише, коли один з множників є рівний нулеві:

x = 0; x - 4 = 0

Отже, маємо два рівняння. Перше вже є розв’язаним:

x = 0

І знайдемо розв’язок другого рівняння:

x - 4 = 0

x = 4

Отже, маємо два розв’язки: «0» та «4».

Зауважимо, що ми маємо суворий знак нерівності («<»), тому, точки на координатній прямій будуть не замальованими (виколотими).

Коефіцієнт «a» є більшим за «0» («a = 1 > 0»), тому, парабола буде вітками в гору. Намалюємо координатну пряму, поставимо на ній точки та побудуємо графік параболи.

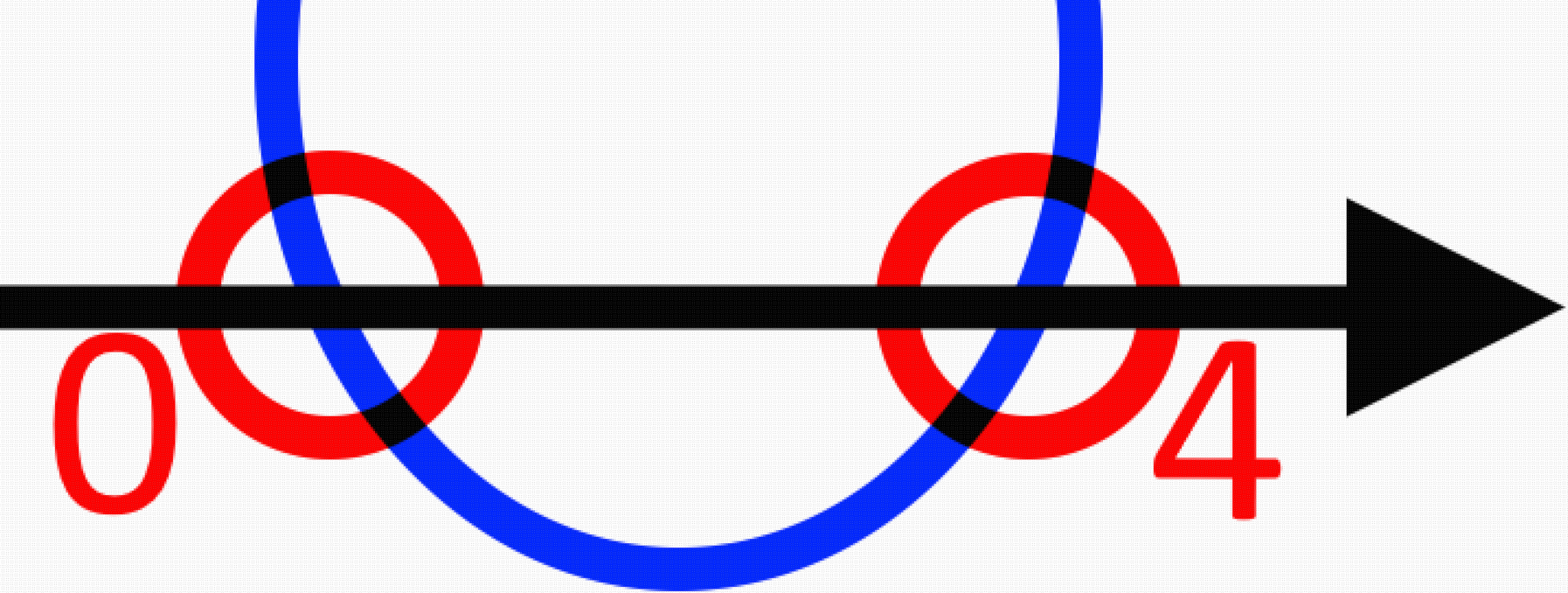
Пам’ятаємо, що проміжки де парабола є над віссю матиме знак «+», а де під віссю матиме знак «-».

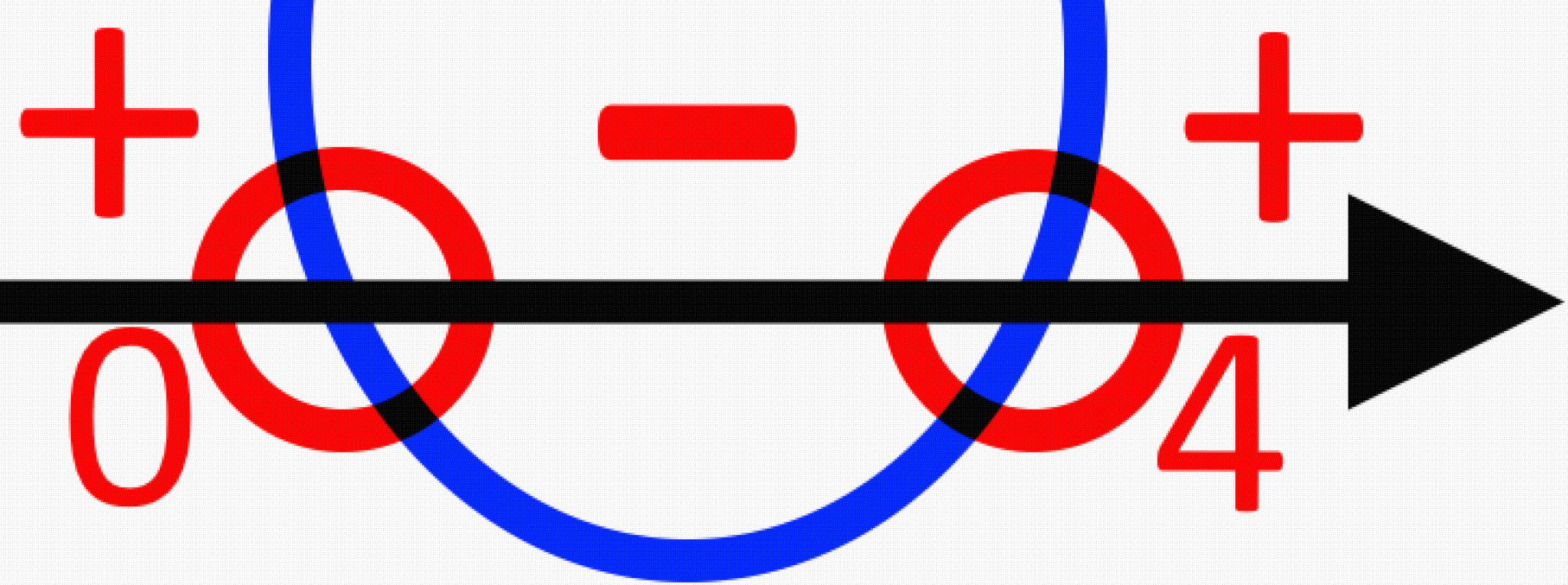
Враховуючи, що наш вираз має бути меншим за нуль, тому, потрібно обрати проміжок зі знаком «-». Також, врахуємо, що маємо суворий знак (не зафарбовані точки), тому у відповіді біля чисел будуть використовуватися круглі дужки. Отже, розв’язком буде:

x ∈ (0; 4)

2) Розв’язати нерівність: «x² ≥ 16».

Для нашої зручності перенесемо все в одну частину. Це необхідно, щоб порівнювати вираз з нулем.

x² - 16 ≥ 0

Тепер, замінимо «≥» на «=».

x² - 16 = 0

Ми отримали не повне квадратне рівняння. Розв’яжемо його. Перенесемо «16» в протилежну частину.

x² = 16

Тепер, нам потрібно добути корінь:

x = ± 16

x = ± 4

Отже, будемо мати два розв’язки: «-4» та «4».

Оскільки, знак нерівності є не суворим «≥», то точки будуть замальованими. А, парабола вітками в гору.

Розставимо знаки проміжків:

Враховуючи, що вираз має бути більшим-рівним за нуль, то потрібно обрати проміжок зі знаком «+», а дужки біля чисел будуть квадратними. Матимемо:

x ∈ (-∞; -4]∪[4; +∞)

3) Розв’язати нерівність: «(x + 3)(x - 3) - 4x ≤ 3».

В нашому випадку ми маємо множення дужок. Ми можемо відкрити дужки оскільки є додавання/віднімання за їх межами:

x² - 9 - 4x ≤ 3

Перенесемо все в одну частину:

x² - 9 - 4x - 3 ≤ 0

Можемо виконати додавання/віднімання подібних чисел:

x² - 4x - 12 ≤ 0

Замінимо знак нерівності на знак рівності:

x² - 4x - 12 = 0

D = (-4)² - 4∙1∙(-12) = 16 + 48 = 64

Розв’язками даного рівняння будуть:

x¹ = #-(-4) + 64#2 ∙ 1 = /4 + 8/2 = /12/2 = 6

x² = #-(-4) - 64#2 ∙ 1 = /4 - 8/2 = /- 4/2 = - 2

Оскільки, знак нерівності є не суворим «≤», то точки будуть замальованими. А, парабола вітками в гору.

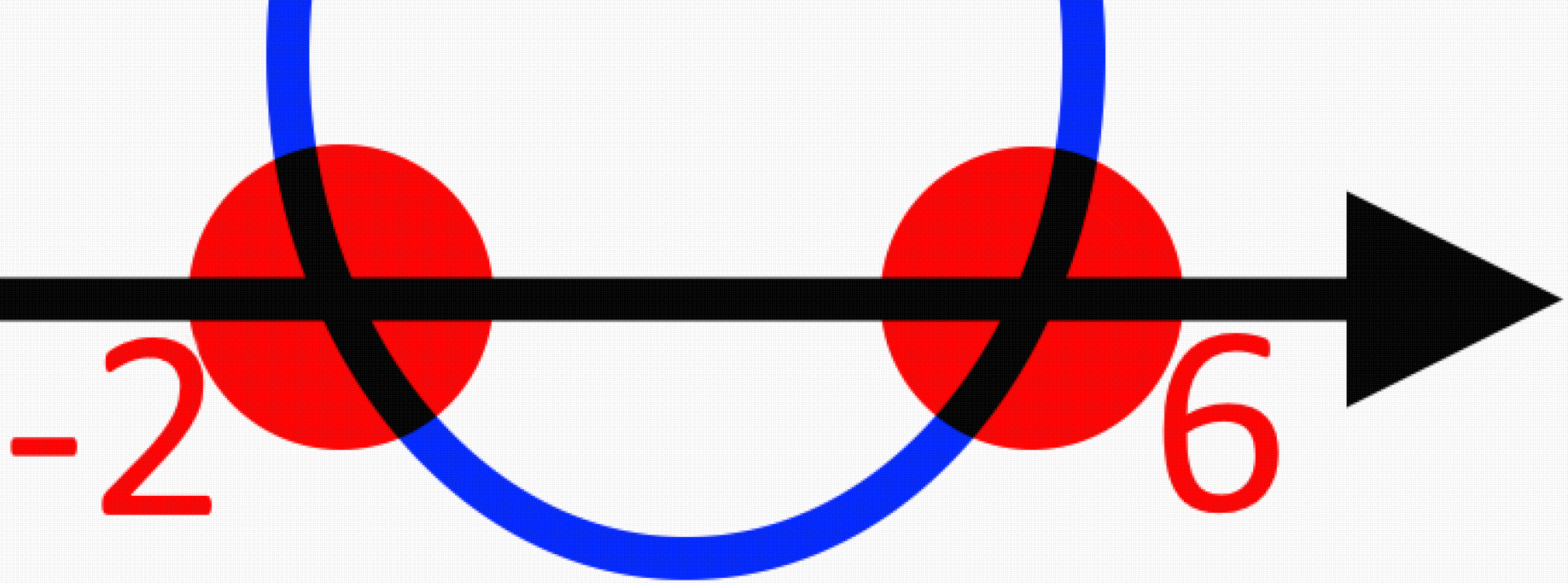
Розставимо знаки проміжків:

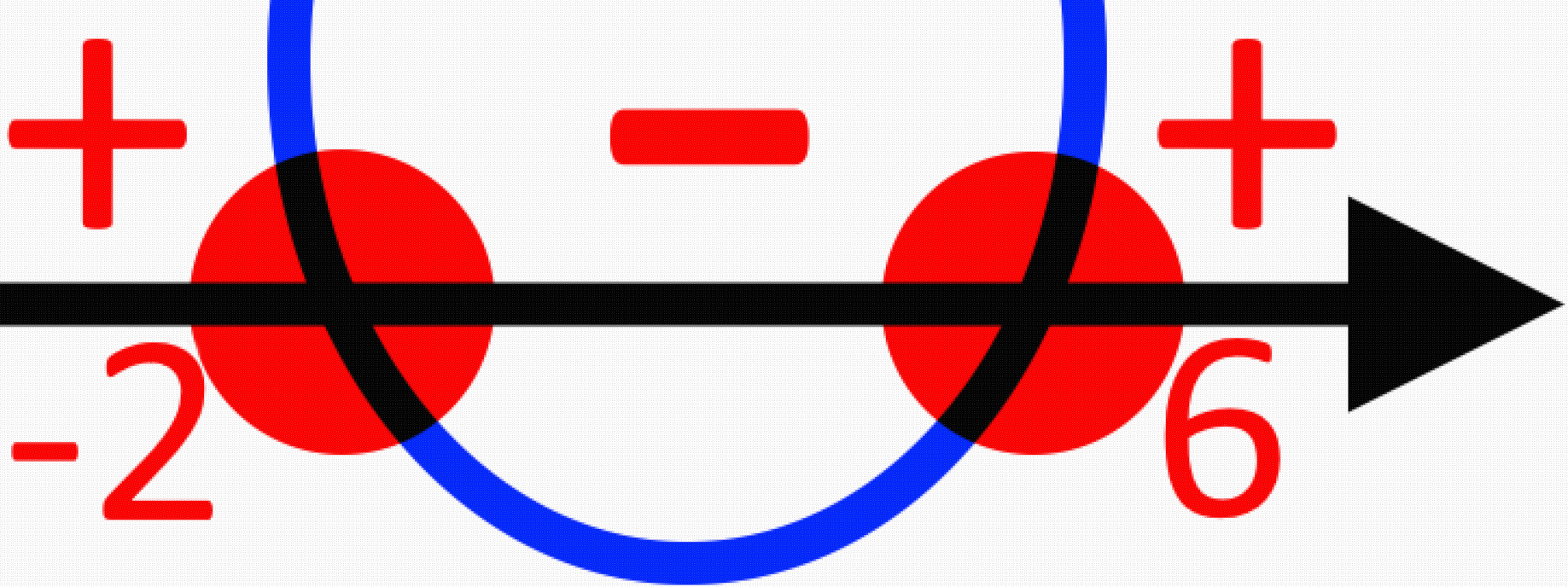
Враховуючи, що вираз має бути меншим-рівним за нуль, то потрібно обрати проміжок зі знаком «-», а дужки біля чисел будуть квадратними. Матимемо:

x ∈ [-2; 6]

4) Розв’язати нерівність: «x² - 6x ≤ -9».

В першу чергу перенесемо все в одну частину:

x² - 6x + 9 ≤ 0

Поміняємо знак нерівності на знак рівності:

x² - 6x + 9 = 0

В реальності тут ми маємо формулу скороченого множення. Скористаємося цим:

(x - 3)² = 0

Та розв’яжемо отримане рівняння. Зауважимо, що дужка рівна «0». Таке можливо лише, коли в дужках є нуль. Тому, матимемо:

x - 3 = 0

x = 3

Оскільки, знак нерівності є не суворим, то точка буде замальованою. Враховуючи, що вона єдина, то парабола буде лише дотикатися до прямої. Парабола буде вітками до гори.

Розставимо знаки проміжків:

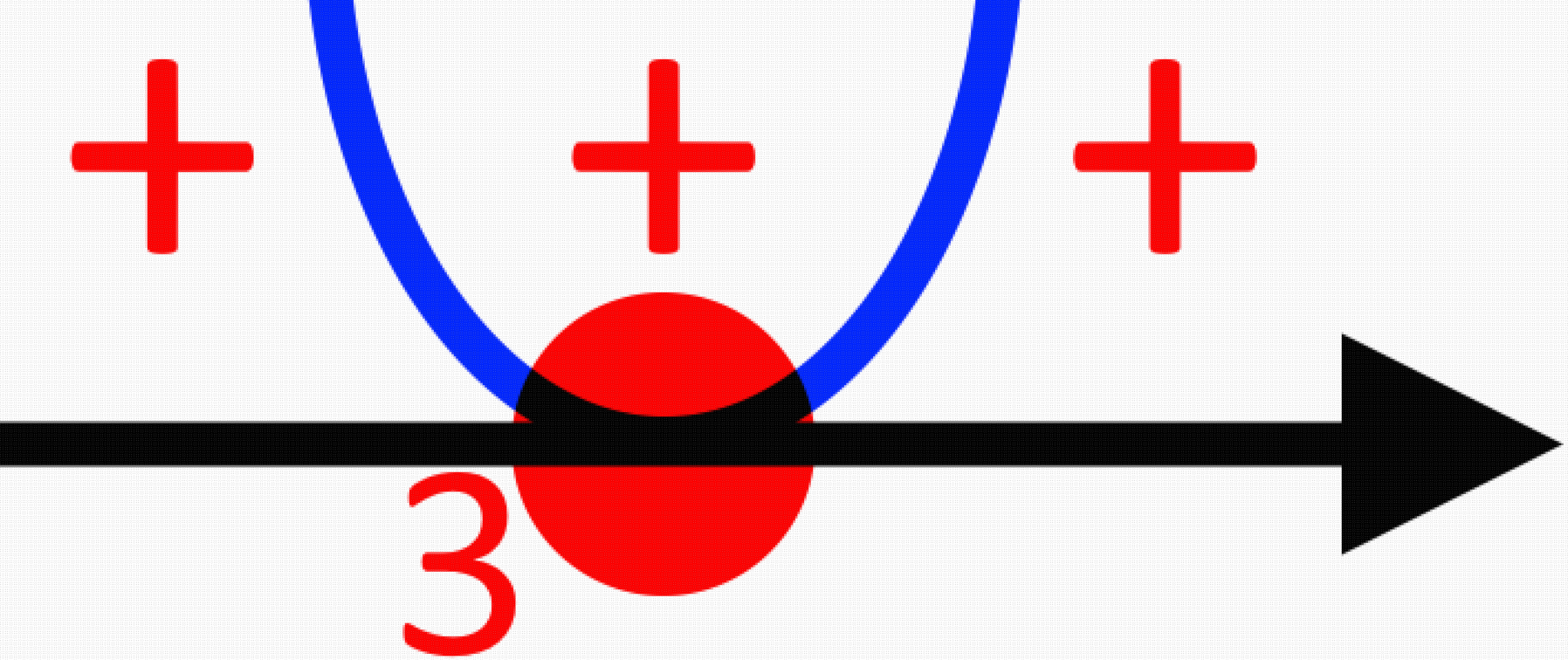
Враховуючи, що знак нерівності є меншим-рівним за нуль, то потрібно обрати проміжки зі знаком «-». Но, ми не маємо таких проміжків, але маємо значення при якому вираз є рівний нулеві. Тому, нерівність матиме єдиний розв’язок, що складається з одного числа.

x ∈ {3}

5) Розв’язати нерівність: «x(x - 5) + 12 < 4 - 5x».

В першу чергу відкриємо дужки:

x² - 5x + 12 < 4 - 5x

Перенесемо все в одну частину:

x² - 5x + 12 - 4 + 5x < 0

x² + 8 < 0

Поміняємо знак нерівності на знак рівності:

x² + 8 = 0

Розв’яжемо отримане рівняння:

x² = -8

x ∈ ∅

Квадратне рівняння не має розв’язків, але це не означає, що квадратна нерівність не має розв’язків. Тому, нам необхідно намалювати координатну пряму. Враховуючи, що рівняння розв’язків не має, то точок на координатній прямій не буде. Ми можемо відразу намалювати параболу, яка буде над координатною прямою (бо парабола вітками в гору).

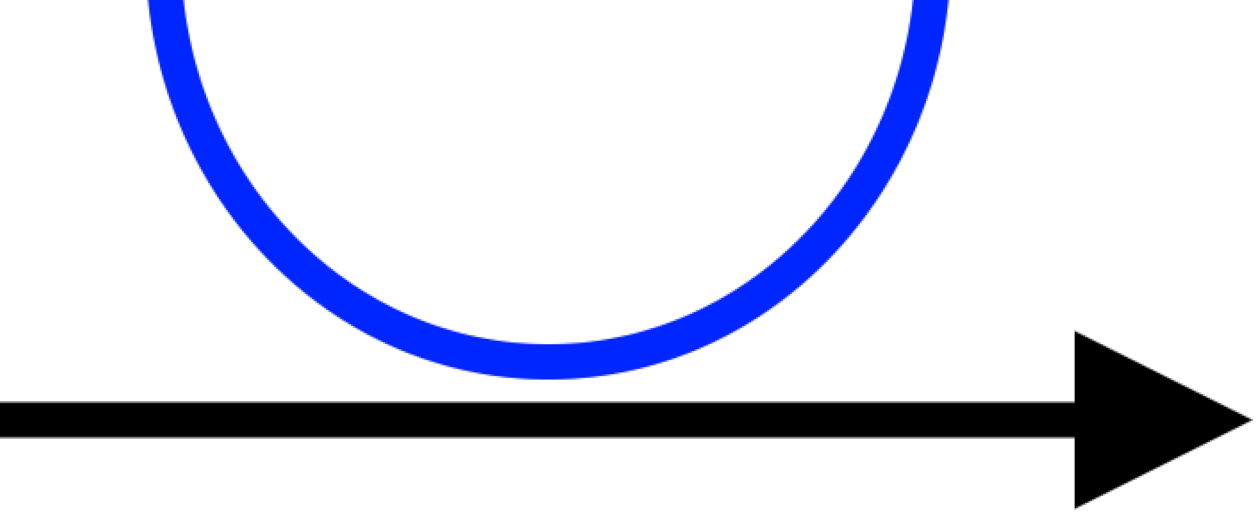
Враховуючи, що ми маємо вираз менший за нуль, то потрібно обрати проміжки зі знаком «-», але в нас їх не має. Тому, нерівність не матиме розв’язків:

x ∈ ∅