Найпростіші геометричні фігури на площині та їх властивості
Площина. Точка і пряма
Площина є однією з основних геометричних фігур. Найпростіший спосіб уявити площину це поглянути на стіл або лист паперу. Тобто, це є плоска, гладка поверхня. Площина в геометрії є рівною, необмеженою та не має товщини.
Основними геометричними фігурами на площині є точка і пряма.
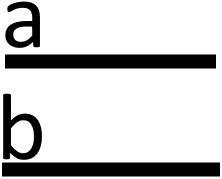
Точки позначають великими латинськими літерами:

Прямі зазвичай позначають маленькою латинськими літерами: При цьому на малюнку зображають лише частину прямої, а всю пряму вважають нескінченою в обидва боки.
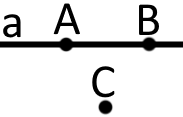
Точки можуть знаходитися (лежать) на прямій або ще можна сказати, що пряма проходить через точки. Намалюємо пряму та позначимо точки та які лежать на прямій (пряма проходить через ці точки), а також точку яка не лежить на прямій Часто використовують скорочене позначення: символ означає тобто можна написати так а символ означає тобто можна записати так
Яка б не була пряма існують точки, що належать цій прямій і точки, що не належать їй.
Через одну єдину точку можна провести безліч прямих.

Для того щоб побудувати пряму достатньо двох точок. Через дві точки можна провести лише одну єдину пряму.

Якщо на прямій є три точки, то лише одна точка може бути між двома іншими. У таких випадках кажуть, що ця точка лежить між двома іншими.
Намалюємо пряму та позначимо на ній точки так, що точка буде лежати між точками та

Пряма розбиває площину на дві півплощини. Це можна порівняти з розрізанням торта на дві частини.
Дві прямі перетинаються, якщо є такі точки однієї прямої які знаходяться у різних півплощинах відносно іншої прямої.

Промінь
Проведемо пряму та позначимо на ній точку

Ця точка ділить пряму на дві частини, кожну з яких разом із точкою називають променем, що виходить з точки Для зручності виділимо їх різними кольорами.

Точка називається початком кожного з променів.
Промені позначають двома великими латинськими буквами, перша з яких є початком променя, а друга – довільна точка, що знаходиться на промені. Продемонструємо промінь

Якщо два промені мають спільний початок та утворюють пряму, то їх називають доповняльними. Наприклад, промені та мають спільний початок в точці і утворюють пряму будуть доповняльними.

Відрізок
Відрізком називають частину прямої, яка складається з усіх точок цієї прямої, що лежать між двома її точками, разом з цими точками. Ці точки називають кінцями відрізка.
Намалюємо пряму та поставимо точки і Після чого отримаємо відрізок який виділимо червоним кольором.

Якщо говорити простими словами, то відрізок це дві точки з’єднаних між собою. Відрізки та

Кожен відрізок має свою довжину, більшу від нуля.
Довжину відрізка називають також відстанню між його кінцями.
Якщо на відрізку позначити ще якісь точки які поділять його ще на відрізки, то довжина початкового відрізку буде рівна сумі відрізків які утворилися після поділу.
Намалюємо відрізок та позначимо на йому точки і так, що точка буде знаходитися між та а між та

В такому випадку довжина відрізка буде складатися з суми відрізків і а довжина відрізку можна буде записати декількома способами: В такий же спосіб можна перевірити чи точки лежать на одній прямій (на одному відрізку), тобто якщо сума (або різниця) двох відрізків буде рівна третьому, то точки які утворюють ці відрізки лежать на одній прямій.
Точку відрізка, яка ділить його навпіл, тобто на два рівні відрізки, називають серединою відрізка.
Ламана
Декілька точок які є послідовно з’єднані між собою (але не утворюють замкнутої фігури) і не лежать на одній прямій утворюють фігуру яка називається ламаною. Точки називаються вершинами ламаної, а відрізки які їх з’єднують називаються ланками ламаної.
ламаної; ламаної.
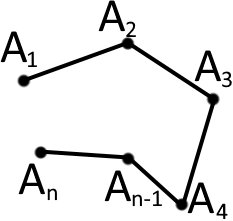
Довжину ламаної можна знайти додавши довжини всіх її ланок.
Довжина ламаної не менша за довжину відрізка, що сполучає її кінці.
Ламана називається простою, якщо вона не має самоперетинів.
Проста ламана

Ламана з самоперетинами
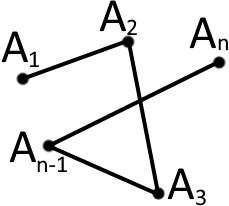
Ламана називається замкнутою, якщо у неї кінці співпадають.

Кут
Кут – це геометрична фігура, яка складається з точки і двох променів, що виходять із цієї точки.
Промені називають сторонами кута, а їх спільний початок – вершиною кута.
Слово позначають (заміняють) символом після чого йде його назва. Кути називають однією або трьома великими літерами латинського алфавіту (Наприклад: чи однією маленькою літерою грецького алфавіту (Наприклад:
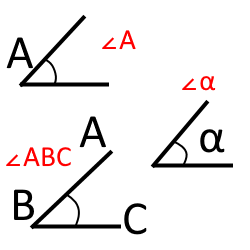
Кут який позначають трьома літерами можна називати по різному. Наприклад може бути або це є різні позначення одного і того ж кута. Єдиний важливий момент це буква яка знаходиться по середині. Вона і є вершиною кута.
Часто також можна замінити назву з трьох букв на одну чи навпаки.

Кут, що на малюнку можна назвати як або
Кут позначають однією літерою, якщо відразу зрозуміло де він знаходиться, а трьома – коли необхідно чітко вказати про який кут йде мова.
Наприклад, на малюнку:
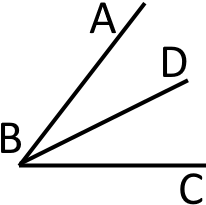
Не буде зрозуміло, що мають на увазі під адже вершина як у кута так і у чи Тому в таких ситуаціях використовують позначення трьома буквами.
Кожен кут має свою градусну міру більшу від нуля. Слово «Градус» чи «Градуси» часто замінюють символом Наприклад:
В залежності від градусної міри кути розрізняють на:
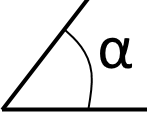
Якщо градусна міра кута є в межах від до то такий кут називається гострим.
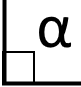
Якщо градусна міра кута рівна то такий кут називається прямим. Прямий кут позначають квадратиком.
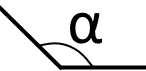
Якщо градусна міра кута є в межах від до при цьому не рівна то такий кут називається тупим.
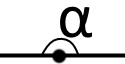
Якщо градусна міра кута рівна то такий кут називається розгорнутим.
Якщо градусна міра кута рівна то такий кут називається складеним.

Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами. Тобто, якщо між сторонами кута провести промінь (поділити початковий кут), то градусна міра початкового кута буде рівна сумі градусних кутів, що утворяться.
Намалюємо кут та проведемо промінь Утвориться два кути і
Після чого будемо мати таку рівність:
∠ABC = ∠ABD + ∠DBC
Або такі:
∠ABD = ∠ABC - ∠DBC
∠DBC = ∠ABC - ∠ABD
Бісектриса кута
Якщо промінь виходить з вершини кута, проходить між його сторонами і ділить його (кут) на два рівні кути (пополам), то цей промінь називають бісектрисою кута або просто бісектрисою.
Часто для того щоб запам’ятати, що таке бісектриса використовують вірш: «Бісектриса це така криса, що бігає по кутам та ділить їх пополам».
Намалюємо та бісектрису

Після чого матимемо:
∠ABO = ∠OBC
∠ABO = /∠ABC/2
∠OBC = /∠ABC/2
Властивість бісектриси кута: будь-яка точка бісектриси кута рівновіддалена від сторін цього кута.
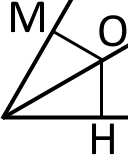
Матимемо:
ОМ = ОН
Суміжні та вертикальні кути
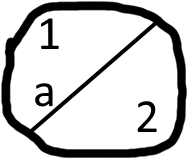
Суміжними кутами називають кути, у яких одна сторона є спільна, а дві інші сторони є доповняльними променями.

Якщо говорити простими словами, то суміжні кути утворюються тоді, коли ми поділимо променем розгорнутий кут. За рахунок цього ми будемо мати наступне твердження: «Сума суміжних кутів завжди рівна Тобто:
∠1 + ∠2 = 180°
В реальності суміжних кутів може бути декілька:
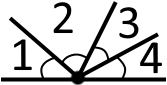
Але твердження, що сума суміжних кутів завжди рівна залишається не зміним.
∠1 + ∠2 + ∠3 + ∠4 = 180°
Вертикальними називають кути, у яких сторони є доповняльними півпрямими.

Якщо говорити простими словами, то вертикальні кути це кути, що утворюються при перетині двох прямих та знаходяться один навпроти одного.
та є вертикальними. Також, кути та
Вертикальні кути між собою рівні. Тобто:
Також варто зауважити, що при перетині двох прямих утворюються як суміжні кути так і вертикальні кути.
Матимемо, що:
- суміжні.
- вертикальні.
Кут між прямими, що перетинаються
Також варто зауважити, що кутом між прямими які перетинаються називають менший із кутів, що утворилися.
Перпендикулярні прямі
Якщо дві прямі перетинаються під прямим кутом, то їх називають перпендикулярними.

Матимемо, що пряма є перпендикулярною до прямої Слово «перпендикулярні» часто заміняють символом Тобто, матимемо:
Перпендикуляр і похила, відстань від точки до прямої
Коли ми маємо пряму та точку яка не лежить на цій прямій і необхідно знайти відстань від цієї точки до прямої. Тоді необхідно провести відрізок який буде перпендикулярним до прямої, а кінцями відрізку будуть дана точка та точка перетину відрізка й прямої. Довжину цього відрізку і називають відстанню від точки до прямої.
Точку перетину прямої та перпендикуляра називають основа перпендикуляра.
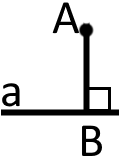
На малюнку ми маємо пряму та відрізок який є перпендикулярним до даної прямої Відстань від точки до прямої буде довжина відрізка
Якщо є пряма та точна яка не лежить на цій прямій, то коли провести НЕ перпендикулярний відрізок, що з’єднає цю точку та пряму, то такий відрізок називатиметься похилою.
Точку перетину прямої та похилої називають основою похилої.
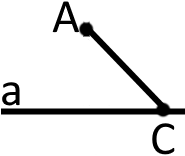
Коли ми матимемо і перпендикуляр (відстань від точки до прямої), і похилу:

Тоді будемо мати такі відрізки:
«а» - пряма.
«АВ» - перпендикуляр до прямої перпендикуляра.
«АС» - похила до прямої похилої.
А відрізок кінцями якого є основа перпендикуляра та основа похилої називають проекцією похилої на пряму. «Проекція» це умовна тінь яку відкидає вітка дерева на землю коли світить сонце.
«ВС» - проекція похилої на пряму
Перпендикуляр та похила мають свої властивості:
1. Перпендикуляр, проведений із даної точки до прямої, менший від будь-якої похилої, проведеної з цієї самої точки до прямої.

AB < AC
2. Якщо дві похилі, проведені до прямої з деякої точки, рівні, то рівні їх проекції.
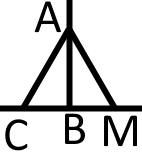
Якщо то
3. Якщо дві похилі, проведені до прямої з деякої точки, мають рівні проекції, то вони рівні.

Якщо то
4. Якщо з даної точки проведено до прямої дві похилі, то більша похила має більшу проекцію на цю пряму.

Якщо то
5. Якщо з даної точки проведено до прямої дві похилі, то більшою з них є та, яка має більшу проекцію на дану пряму.

Якщо то
Серединний перпендикуляр
Серединним перпендикуляром до відрізка називають пряму (або відрізок), яка проходить через середину даного відрізка і є перпендикулярною до нього.
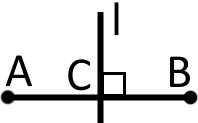
перпендикуляр до відрізка Звідси маємо, що:
Також ми маємо властивість серединного перпендикуляра, а саме: «кожна точка, що належить серединному перпендикулярові є рівновіддалена (знаходиться на однаковій відстані) від кінців відрізка.
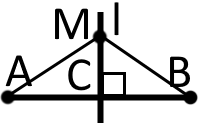
Матимемо:
Паралельні прямі
Дві прямі на площині називаються паралельними, якщо вони не перетинаються. Слово «паралельні» заміняють символом
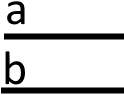
Будемо мати, що прямі та є паралельними, тобто
Кути, утворені при перетині двох прямих січною
Пряму називають січною відносно двох інших прямих, якщо вона перетинає ці прямі.

Пряма є січною відносно прямої та
Як помітно, при перетині двох прямих січною утвориться вісім кутів. Позначимо їх.

Тут варто уточнити деякі моменти. Як помітно частина кутів (кути знаходиться між прямими їх називають внутрішніми відповідно через те, що вони в середині. А решту кутів (кути називають зовнішніми, бо вони за межами. Також кути мають свою назву відносно розміщення щодо січної Якщо вони розміщені по одну сторону (наприклад, кути або кути то їх називають односторонніми, а якщо по різні сторони (наприклад, кути то різносторонніми. А кути, що знаходяться на однакових місцях (наприклад, кути та знаходяться ліворуч зверху) називають відповідними.
Отже, наші кути будуть такими:
Внутрішні односторонні:
Внутрішні різносторонні: Кути та вважають суміжними!
Відповідні:
Ми не зачіпали зовнішні кути через те, що їх майже ніколи не використовують у задачах.
Ознаки та властивості паралельності прямих
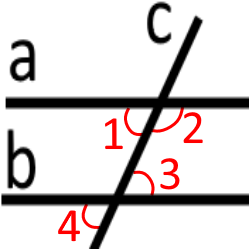
Дві прямі які перетинаються січною є паралельними, виконується одна з умов:
Внутрішні різносторонні кути рівні:
Відповідні кути рівні:
Сума внутрішніх односторонніх кутів дорівнюють
Тоді будемо мати:
Якщо дві прямі є перпендикулярними до третьої прямої, то ці прямі між собою є паралельними.
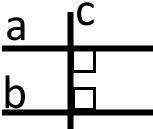
Якщо і то
Якщо дві прямі є паралельними до третьої прямої, то ці прямі між собою є паралельними.
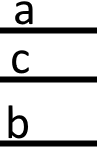
Якщо і то
Відстань між паралельними прямими
Відстанню між паралельними прямими називають довжину їх спільного перпендикуляра.
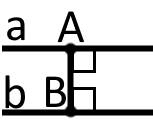
прямі, де і між прямими.
Аксіоми планіметрії
Аксіоми планіметрії – це твердження про основні властивості найпростіших геометричних фігур, прийняті як вихідні положення.
Більшість з аксіом планіметрії ми вже розглянули. В даному розділі просто їх пригадаємо.
1. Якою б не була пряма, існують точки, які належать їй та які не належать їй.
2. Через будь-які дві точки можна провести пряму, і тільки одну.
3. З трьох точок, що лежать на одній прямій лише одна і тільки одна знаходиться між двома іншими.
4. Пряма розбиває площину на дві півплощини.
5. Дві прямі перетинаються тоді, коли точки, що належать одній прямій знаходяться у різних півплощинах відносно другої прямої.
6. Кожен відрізок має певну довжину, більшу нуля.
7. Довжина відрізка дорівнює сумі довжин частин, на які розбивається відрізок будь-якою своєю точкою.
8. Відстань між двома точками – це довжина відрізка, що сполучає ці точки.
9. Кожний кут має певну градусну міру, більшу нуля. Розгорнутий кут дорівнює
10. Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що має початок у вершині кута та проходить між його сторонами.
11. Через точку, що не лежить на даній прямій, можна провести одну пряму, паралельну даній.