Означення конуса. Елементи конуса

Конус це геометричне тіло, утворене обертанням прямокутного трикутника навколо одно з його катетів. Також, конус може утворитися в наслідок обертання рівнобедреного трикутника навколо висоти проведеної до основи трикутника (або рівностороннього трикутника навколо будь-якої висоти).

Розглянемо прямокутний трикутник «АВС» з прямим кутом «В». Та будемо обертати наш трикутник навколо катета «АВ».

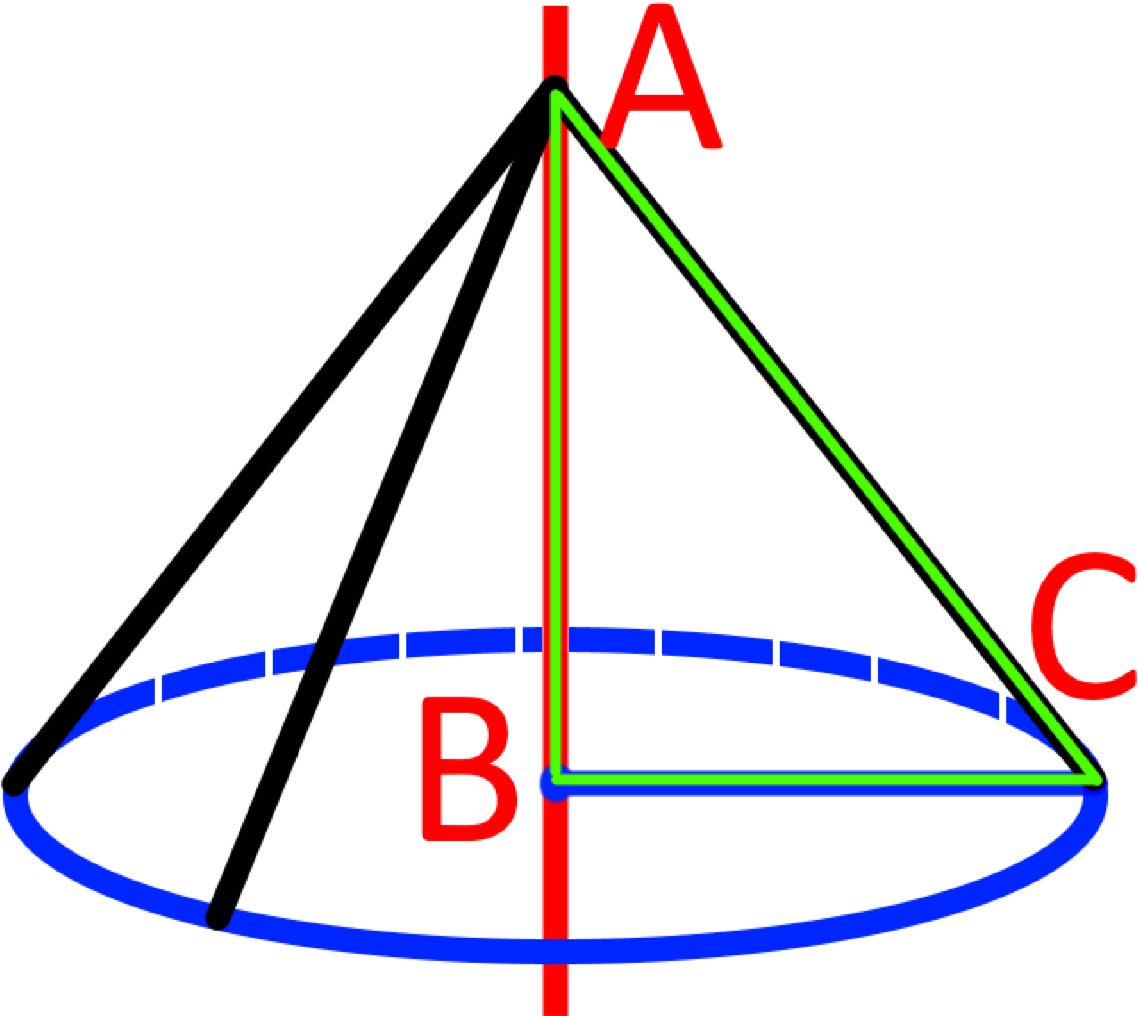
Як помітно, в результаті обертання у нас утворюється конус. Розглянемо елементи даного конуса.

Ми обертали конус навколо катета «АВ», тому цей катет буде «висотою» даного конуса («AB = h»). А, також, буде «віссю обертання» (або «віссю конуса»). Катет «ВС» буде описувати круг який називають «основою конуса» і даний катет буде «радіусом основи» («BC = r»). При цьому прямий кут (кут «В») буде «центром основи», тобто «центром кола/круга» утвореного під час обертання. А, вершина трикутника «А» буде «вершиною конуса». Гіпотенуза «АС» називається «твірною конуса» («AC = l»). Поверхня яка утвориться в результаті обертання гіпотенузи (твірної) буде називатися «бічною поверхнею конуса».

Перерізи конуса

Конус можна перерізати великою кількістю способів. Розглянемо основні типи перерізу.

Якщо переріз конуса проходить через його вісь (вісь обертання), то його називають «осьовим перерізом конуса». Даний переріз буде мати форму рівнобедреного трикутника основа якого є діаметром кола, яке лежить в основі, а бічні сторони є твірними конуса.

Також, переріз може проходити через вершину конуса, але не проходити через його твірну. В такому випадку ми також будемо мати рівнобедрений трикутник, де бічні сторони будуть твірними конуса, а його основа буде хордою основи конуса.

Якщо переріз є перпендикулярним до осі конуса (паралельним до його основи), то переріз буде мати форму круга. Центр даного круга буде знаходитися в точці перетину даної площини та осі конуса.

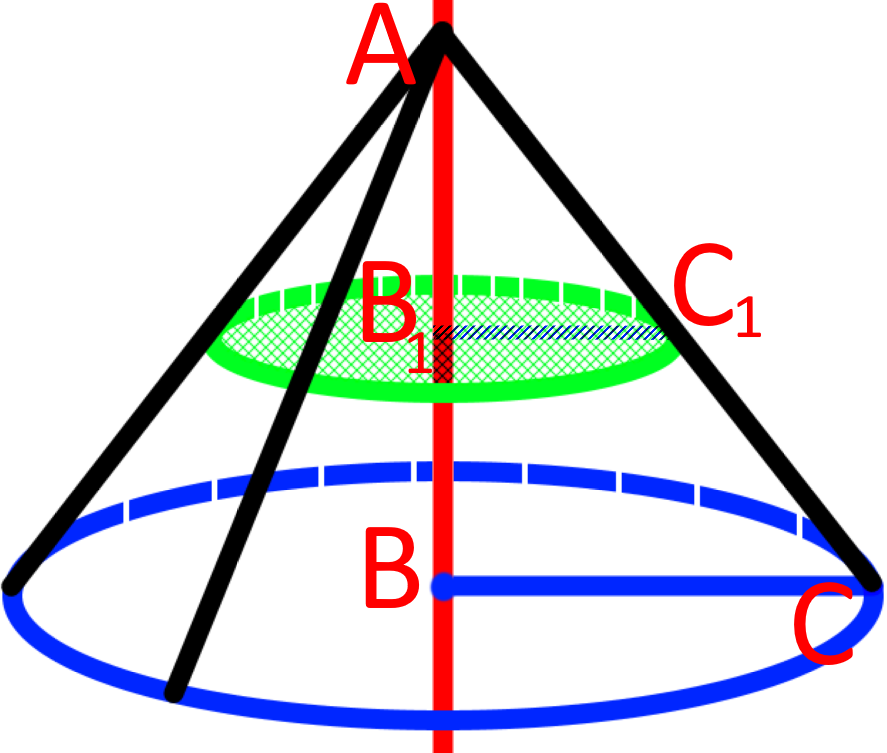
Зауважимо, що круг який утворився при перерізі буде подібним до круга основи. При цьому ми будемо мати подібні конуса. Тобто, конуси утворені трикутниками «AB₁ C₁» та «ABC» будуть мати властивості подібних фігур.

При цьому, якщо відкинути верхню частину, то ми отримаємо «зрізаний конус». І, якщо, провести переріз паралельний до осі (або через вісь), то ми отримаємо рівнобічну трапецію.

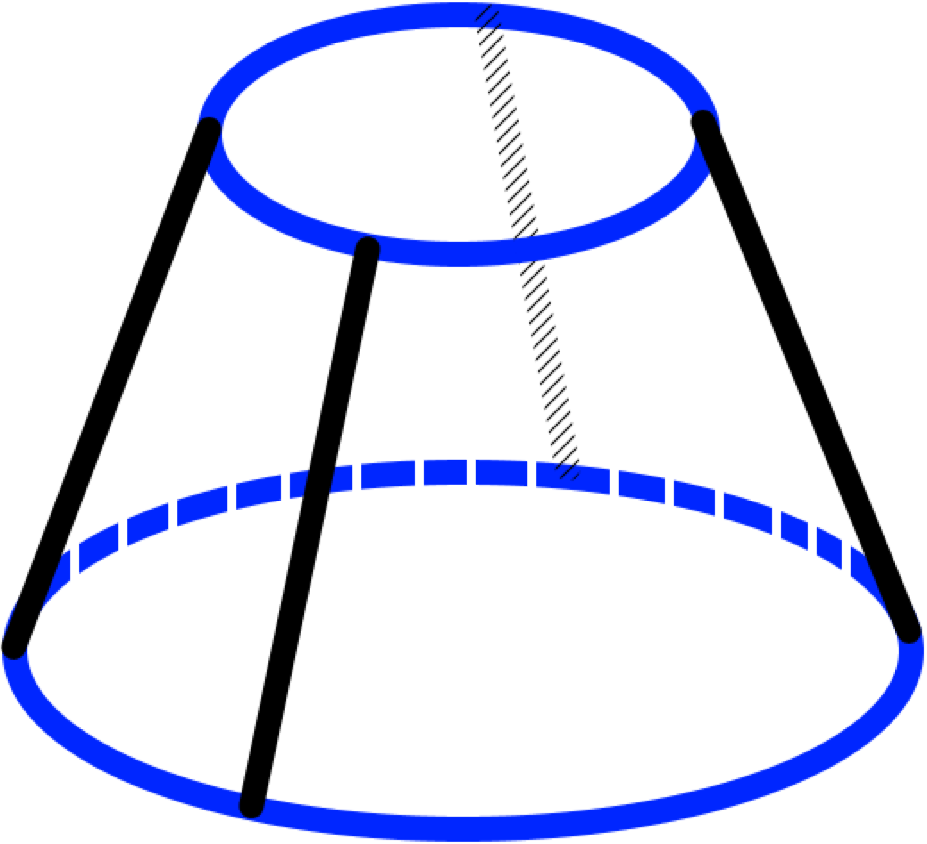
Площі конуса

У циліндрі як і в багатьох об’ємних фігурах розрізняють три типи площі.

Площа основи. Площу основи позначають «S_o». Враховуючи, що в основі конуса знаходиться коло, то й відповідно площу основи можна знайти за формулою площі кола:

S_o = πr² = πd²4

Площа бічної поверхні. Площу бічної поверхні (або просто бічну поверхню) позначають «S_б». Ви могли бачити фігури у вигляді конуса. Для прикладу це може бути ковпак який використовують при святкуванні дня народження. Ще часто шляпи чаклунів у фільмах мають форму конуса. Або, для прикладу, це може бути дорожній конус.

Якщо взяти конус і розрізати його по твірній, то його розгортка буде у формі дуги кола (частиною кола).

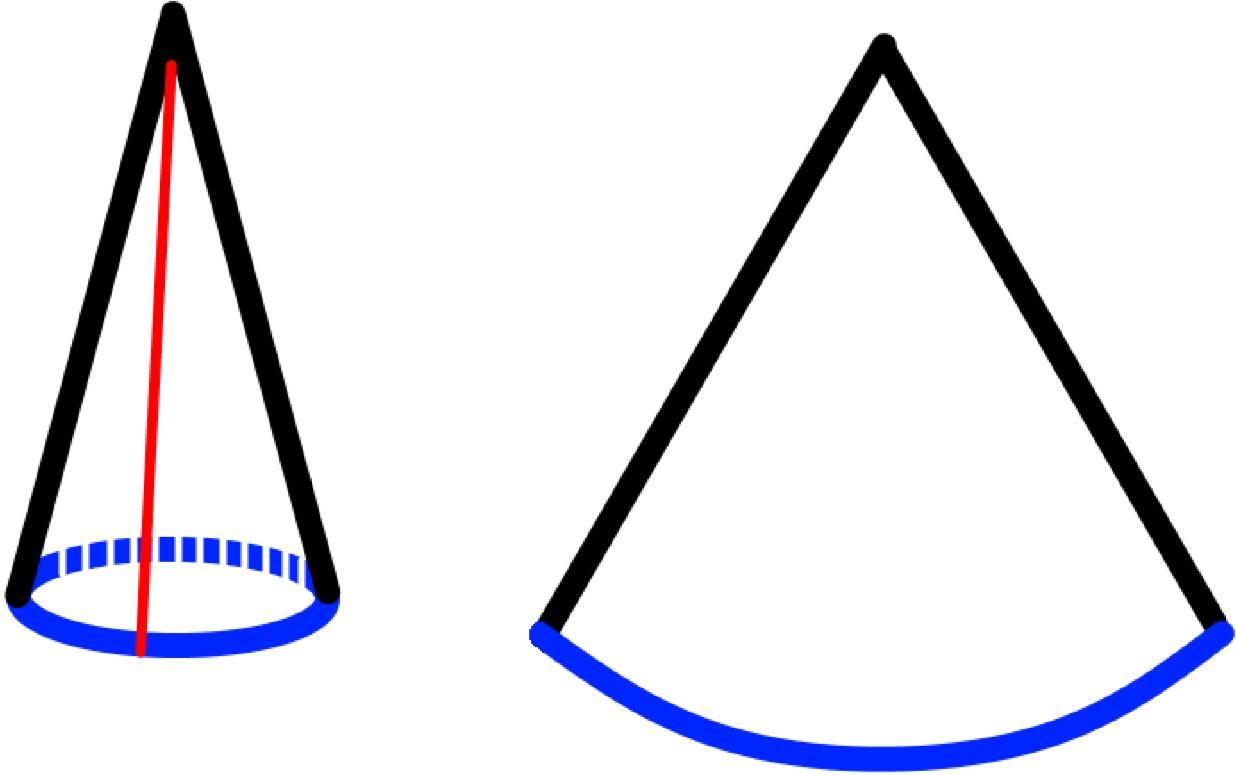
Розглянемо розгортку конуса:

Бічну поверхню конуса можна знайти за формулою:

S_б = πrl

Або, якщо розглядати її (розгортку бічної поверхні) як дугу, то можна скористатися формулою площі сектора:

S_б = πl²n360

Площа повної поверхні. Площу повної поверхні (або просто повну поверхню) позначають «S_п». Площу повної поверхні можна знайти як суму площі бічної поверхні та площі основи.

S_п = S_б + S_o

Ми можемо підставити формули площ бічної поверхні та основи й отримаємо:

S_п = πrl + πr² = πr(l + r)

Об’єм конуса

Об’єм конуса як і в багатьох фігурах позначають «V».

Для того щоб знайти об’єм конуса необхідно помножити одну третю на площу основи циліндра «S_o» на його висоту «h».

V = /1/3S_oh = /1/3πr²h