Дослідження функції за допомогою похідної
Побудувавши графік функції ви можете помітити, що в деяких місцях дана функція піднімається до гори, а в деяких йде до низу. Десь вона знаходиться над віссю а десь під віссю. А, в деяких місцях функція може мати точки розриву або взагалі не існувати.
В даному уроці ми навчимося досліджувати функцію не будуючи її графік. Але ознайомтеся з правилами обчислення похідних.
Давайте виділимо всі кроки дослідження функції. Вони йдуть послідовно і якщо вам необхідно виконати в завданні крок «5», то це означає, що потрібно виконати всі попередні кроки. Деякі кроки є не важливими, тому про це буде наголошено.
Кроки дослідження функції:
1) Знаходимо область визначення функції. (Часто цей крок пропускають, але таке робити не варто).
2) Знаходимо точки перетину графіку функції з осями координат. (Даний етап необхідний для побудови графіку, але для дослідження не грає великої ролі).
3) Досліджуємо функцію на парність/не парність. (Крок є не обов’язковим, тому його зазвичай пропускають).
4) Знаходимо похідну функції. Це необхідно для наступних кроків.
5) Знаходимо критичні точки.
6) Знаходимо проміжки монотонності. Це проміжки зростання та спадання функції.
7) Знаходимо точки екстремумів.
8) Знаходимо точки мінімуму та максимуму функції.
9) Знаходимо максимум та мінімум функції.
10) При потребі шукаємо максимум та мінімум функції на заданому проміжку.
Є ще важливі кроки, які розглядають в більш поглиблених випадках. Ми в них розберемося і вони також будуть записані в послідовності виконання.
Критичні точки
Критичні точки це точки в яких похідна даної функції не існує (наприклад, якщо в похідній є знаменник) або рівна нулеві рівняння
Тобто, щоб знайти критичні точки, потрібно похідну функції прирівняти до нуля та отримане рівняння. Всі (значення при яких похідна рівна нулеві) та (значення при яких похідна функції не існує) і будуть критичними точками.
Зверніть увагу, що на графіку ми маємо функції. Точки в яких відбуваються такі ситуації називають критичними точками.
Тобто, на графіку критичні точки можуть виглядати:
«Перегин» - плавний перехід функції.
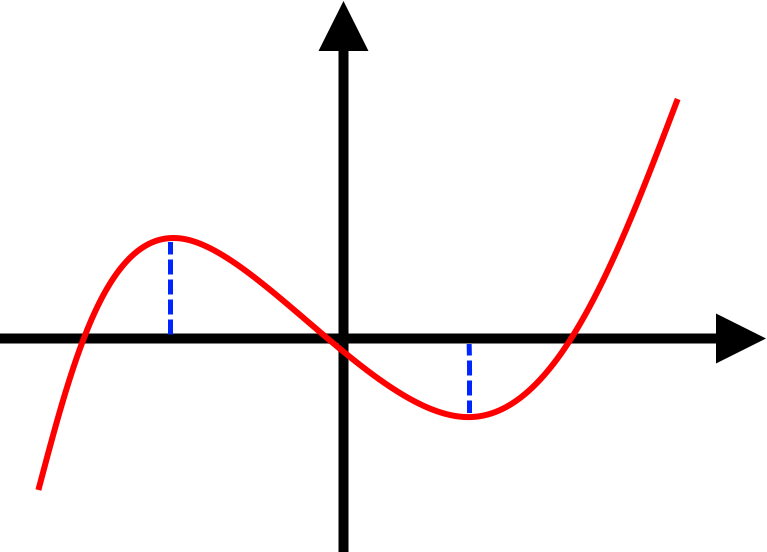
«Злам» - різкий перехід функції.
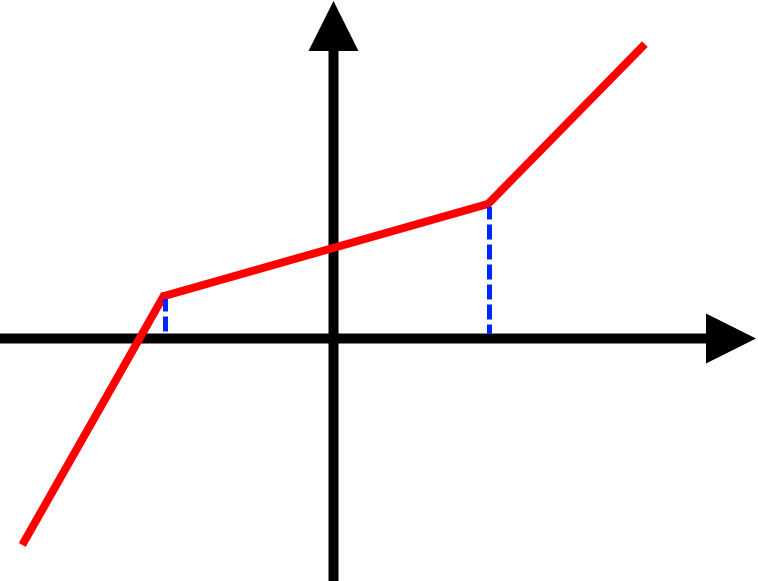
«Розрив» - розрив функції в певній точці.
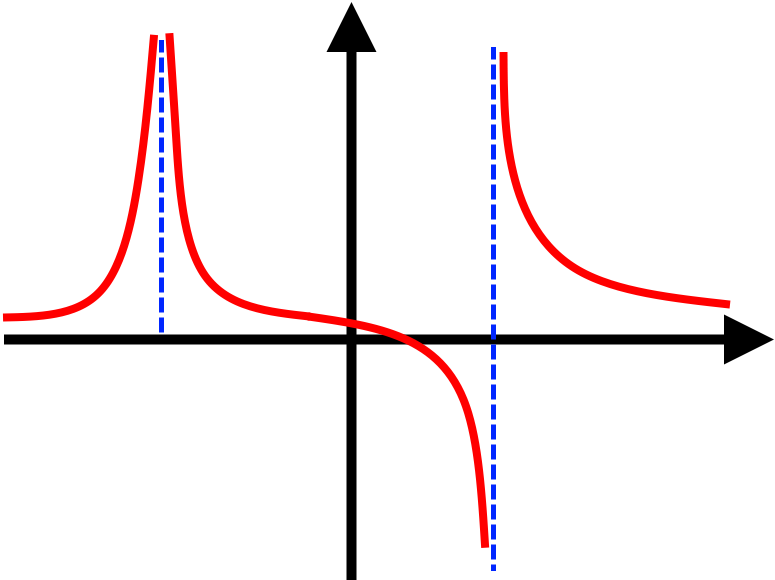
Проміжки монотонності. Проміжки зростання та спадання функції
Проміжки на яких функція зростає чи спадає, називають проміжками монотонності.
Функція зростає на заданому проміжку, якщо більшому значенні аргументу функції відповідає більше значення функції:
При матимемо
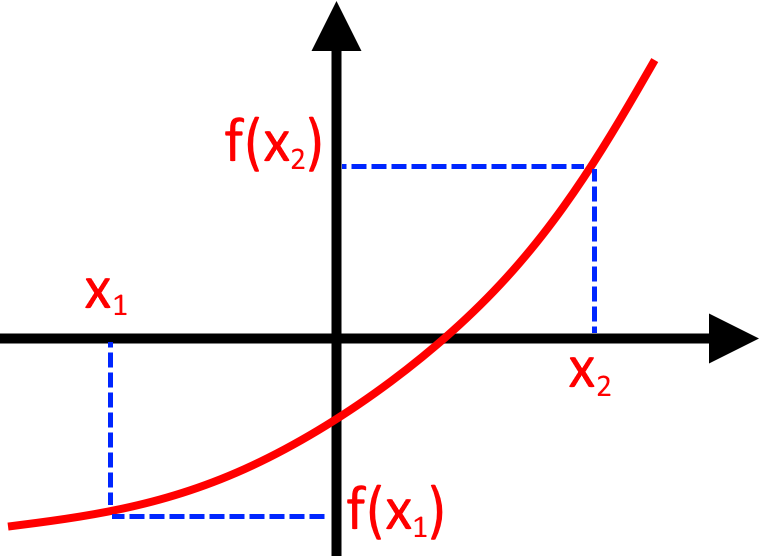
Достатньою умовою зростання функції є:
Якщо у функції на проміжку в кожній точці даного проміжку, значення похідної буде більше нуля, то функція зростає на даному проміжку:
f'(x) > 0
Функція спадає на заданому проміжку, якщо більшому значенні аргументу функції відповідає менше значення функції:
При матимемо
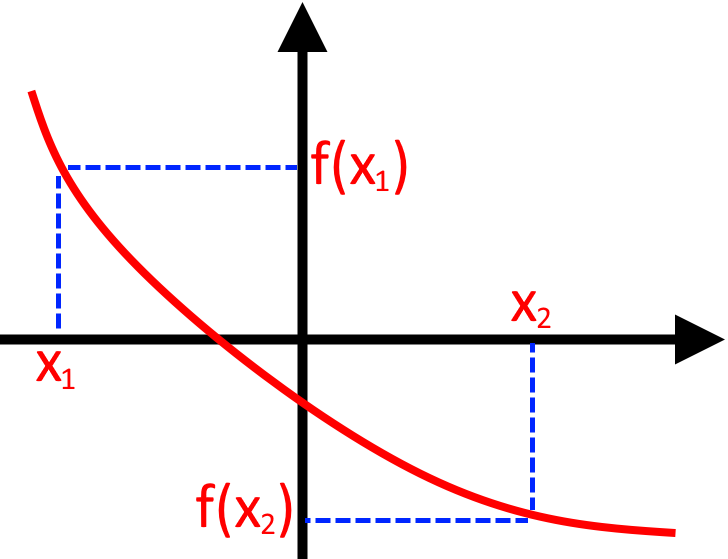
Достатньою умовою спадання функції є:
Якщо у функції на проміжку в кожній точці даного проміжку, значення похідної буде менше нуля, то функція спадає на даному проміжку:
f'(x) < 0
Якщо ви хочете дослідити функцію на проміжки то вам необхідно нанести критичні точки на координатну пряму і знайти знак кожного проміжку, які входять в область визначення
Проміжки зі знаком є проміжками зростання функції, проміжки зі знаком є проміжками спадання функції. Для зручності проміжки зі знаком позначають (зростання), а зі знаком позначають
Завдання. Знайти проміжки зростання та спадання функції
Для знаходження проміжків зростання та спадання функції скористаємося схемою описаною вище.
1) Дана функція не має обмежень, тому її область визначення є:
D(y) ∈ (-∞; +∞)
2) Знаходимо похідну функції:
3) Прирівняємо отриману похідну до нуля, та розв’яжемо отримане рівняння:
2x∙ex + x2∙ex = 0
x∙ex(2 + x) = 0
x = 0;
Отже, матимемо такі розв’язки.
Перший розв’язок:
x = 0
Другий:
ex = 0
x ∈ ∅
Третій:
2 + x = 0
x = -2
4) Потрібно отримані розв’язки та нанести на координатну пряму. Не не має.

Отже, маємо три проміжки:
5) Знаходимо знак похідної на кожному проміжку. Для цього ми можемо взяти якесь число з кожного проміжку та підставити це число в нашу похідну. Якщо в результаті отримаємо додатне число, то проміжок має знак Якщо результат буде то проміжок буде зі знаком
Візьмемо похідну у вигляді:
x ∙ ex · (2 + x)
Розглянемо перший проміжок та візьмемо число
#3#e3 > 0
Відповідно, отриманий результат є більший за тому даний проміжок матиме знак
На другому проміжку візьмемо
-/1/e < 0
Відповідно, отриманий результат є меншим за тому даний проміжок матиме знак
На третьому проміжку візьмемо
→ →
3e > 0
Відповідно, отриманий результат є більший за тому даний проміжок матиме знак
Отже, матимемо такі знаки на проміжках:
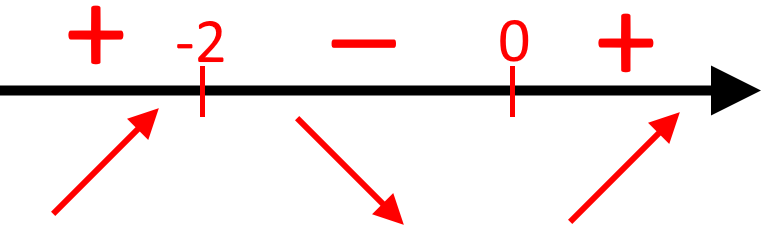
6) Залишається записати відповідь.
Проміжки зростання на координатній прямій мають знак тому:
↗: (-∞; -2) ∪ (0; +∞)
Проміжки спадання на координатній прямій мають знак тому:
↘: (-2; 0)
Точки екстремумів функції
Точки екстремумів функції це критичні точки в яких значення змінної (аргументу функції) похідна функції змінює свій знак на протилежний.
Тобто, точки екстремумів це критичні точки, які знаходяться між двома РІЗНИМИ знаками на координатній прямій.
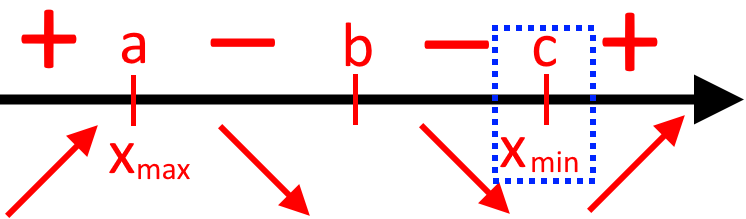
На координатній прямій дані точки виглядатимуть так:
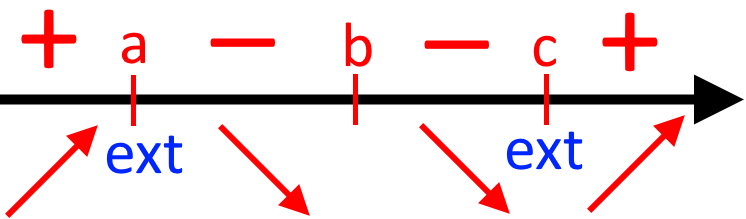
На графіку функції точки екстремумів виглядають лише як перегини функції.

Точки максимуму та мінімуму функції
Точки максимуму та мінімуму функції це точки екстремуму.
Точка максимуму це екстремум функції який знаходиться між знаками та (саме в такому порядку). А, на графіку це перегин з вершиною в гору (тобто, коли функція має таку поведінку
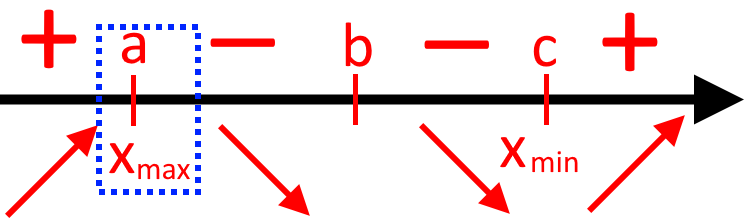
Точка мінімуму це екстремум функції який знаходиться між знаками та (саме в такому порядку). А, на графіку це перегин з вершиною до низу (тобто, коли функція має таку поведінку
Завдання. Знайти точки екстремумів функції:
В першу чергу зауважимо, що не може бути рівний Оскільки знаменник не може бути рівний Тобто, область визначення функції буде:
D(y) ∈ (-∞; 0) ∪ (0; +∞)
При цьому, в реальності не завжди є сенс шукати в першу чергу область визначення функції. Зазвичай, область визначення похідної буде збігатися з областю визначення початкової функції. Але, не варто цим нехтувати!
Тепер, знайдемо похідну функції:
Прирівняємо похідну до нуля та розв’яжемо отримане рівняння:
1 - #16#x2 = 0
Дане рівняння є дробово-раціонального типу. Помножимо дане рівняння на
1 - #16#x2 = 0 | ∙ x2
Отримаємо рівняння:
x2 - 16 = 0
x2 = 16
x = ± 16
x = ±4
Та не рівняння (не бо знаменник не може бути рівний нулеві).
x2 ≠ 0
x ≠ 0
Отже, ми отримали такі критичні точки:
Позначимо дані точки на координатній прямій.

Як помітно, ми отримали декілька проміжків:
Знайдемо знак кожного проміжку. Для цього можна скористатися методом інтервалів. Або, ви можете підставити якесь число з кожного проміжку та знайти знак проміжку. що проміжки зі знаком це проміжки зростання функції, а зі знаком проміжки спадання функції.
Зробіть це самостійно та перевірте чи збіглися наші результати:
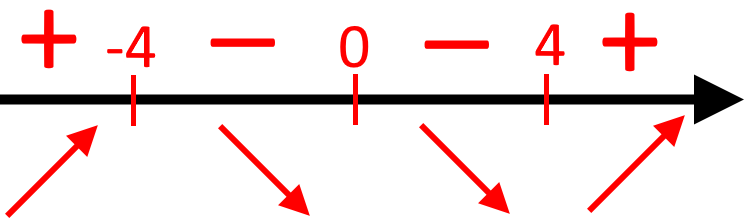
Як бачите, число знаходиться між знаками та (між стрілками та Тому, буде точкою максимуму функції.
xmax = -4
Точка знаходиться між двома однаковими знаками. Тому, вона не є точкою екстремуму функції.
Точка знаходиться між знаками та (між стрілками та Тому, буде точкою мінімуму функції.
xmin = 4
Екстремуми функції. Максимум та мінімум функції
Екстремум функції це значення функції в точці екстремуму (зауважте, що тут не має слова ТОЧКА).
Відповідно, максимум функції це значення функції в точці максимуму функції.
fmax = f(xmax)
Відповідно, мінімум функції це значення функції в точці мінімуму функції.
fmin = f(xmin)
Демонстрація максимального та мінімального значення функції:
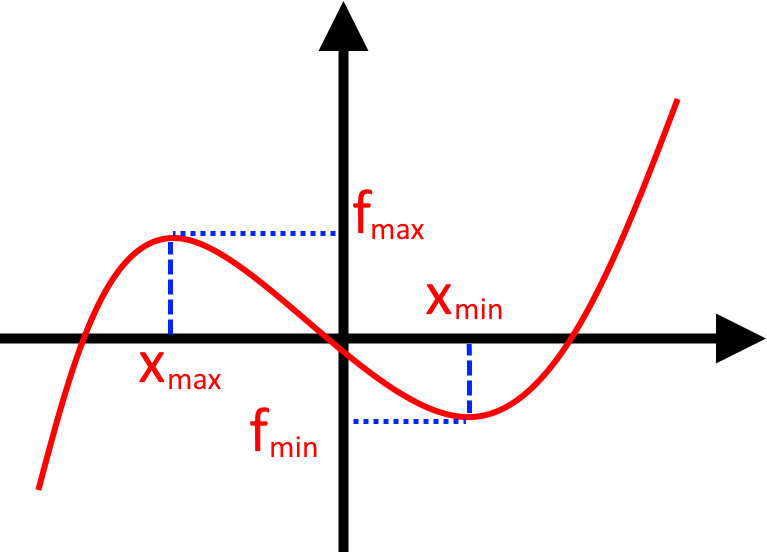
Візьмемо функцію з попереднього завдання «y = x + #16#x».
Пригадаємо, що:
xmax = -4
xmin = 4
Отже, максимум функції буде такий:
Мінімум функції буде:
Знаходження найбільшого і найменшого значення функції на відрізку
Якщо ми маємо не перервну функцію на проміжку то функція буде набувати найбільшого та найменшого значення на даному проміжку.
Для того щоб знайти найбільше та найменше значення функції на даному проміжку, варто скористатися такою послідовністю дій:
1) Перевіряємо чи заданий проміжок входить в область визначення функції.
2) Знаходимо похідну функції.
3) Знаходимо критичні точки.
4) Обираємо критичні точки, які належать заданому проміжку.
5) Обчислюємо значення функції у вибраних критичних точках та в кінцях проміжку точках та
6) Порівнюємо отримані результати. Знаходимо відповідно найбільше та найменше значення функції серед отриманих результатів.
7) Записуємо відповідь.
Завдання. Знайти найбільше та найменше значення функції на проміжку
1) Наша функція є неперервною на всій області визначення (не має знаменника чи кореня парного степеня).
D(y) ∈ (-∞; +∞)
2) Знайдемо похідну даної функції:
(x2 - 3x)' = 2x - 3
3) Знаходимо критичні точки. Для цього потрібно похідну прирівняти до нуля та отримане рівняння.
2x - 3 = 0
2x = 3
x = /3/2
x = 1,5
Зауважимо, що вам не шукати точки екстремумів (точки мінімуму та максимуму). Хоча, якщо, вам потрібно знайти конкретно мінімум чи максимум функції, то можна буде не підставляти зайві числа для обчислення.
4) Оскільки належить проміжку то дану критичну точку будемо враховувати при пошуках найбільшого та найменшого значення.
5) Обчислимо значення функції в наших критичних точках та на кінцях заданого проміжку.
y(1,5) =
y(0) = 02 - 3 ∙ 0 = 0
y(2) = 22 - 3 ∙ 2 =
6) Порівнюємо отримані результати. Найменше значення функції є Відповідно, це є найменше значення функції. Найбільшим значенням функції є
7) Відповідь:
ymin = -2
ymax = 0
Додаткова інформація!
Друга похідна
Після того як ви обчислите похідну від вашої функції, то можна обчислити ще одну похідну від отриманого результату. Це називається друга похідна. Дану похідну можна записати так:
Приклад. Обчислити другу похідну функції
Обчислимо першу похідну функції:
Тепер, треба обчислити ще одну похідну від отриманого результату:
Отже, друга похідна від початкової функції буде:
y'' = 3x + cos x
Опуклість функції
Друга похідна функції використовується для знаходження опуклості функції на заданому проміжку.
Якщо для всіх значень на якомусь проміжку виконується нерівність то функція є опуклою вниз на даному проміжку.
Якщо для всіх значень на якомусь проміжку виконується нерівність то функція є опуклою вгору на даному проміжку.
Точки перегину
Для того, щоб знайти точки перегину функції то потрібно знайти другу похідну функції та обчислити рівняння Після чого, потрібно перевірити чи друга похідна функції змінює свій знак при переході через дані точки.
Приклад: дослідити функцію на опуклість та точки перегину.
Для знаходження опуклості функції та точок перегину потрібно в першу чергу знайти область визначення функції.
Дана функція є визначеною на всій дійсній множині:
D(y) : x ∈ R
Тепер, знайдемо першу похідну функції:
Тепер, знайдемо другу похідну функції:
Прирівняємо другу похідну до нуля:
60x3 - 120x2 + 60x = 0
Та розв'яжемо отримане рівняння:
60x3 - 120x2 + 60x = 0 | ∶ 60
x3 - 2x2 + x = 0
x(x2 - 2x + 1) = 0
x = 0; або
Маємо два рівняння. Перше рівняння вже є ще друге:
x2 - 2x + 1 = 0
(x - 1)2 = 0
x - 1 = 0
x = 1
Отже, маємо числову пряму, яка розбивається числами та на проміжки:

Знайдемо знаки другої похідної. Для цього можна підставити числа з даних проміжків в другу похідну та знайдемо знак результату.
y''(-1) =
y''(/1/2) =
y''(1) =

Отримали проміжок який є проміжком опуклості (функція вигнута вгору), бо Та, два проміжки випуклості (функція вигнута до низу), бо
Оскільки, в точці друга похідна функції змінює знак, то це є абсциса точки перегину (значення по осі Залишається підставити дане значення у функцію та знайти ординату точки перегину.
y(0) = 3∙05 - 10∙04 + 10∙03 + 12∙0 + 3 = 3
Отже, точка є точкою перегину.