Для того щоб успішно розв’язувати практичні завдання вам варто ознайомитися з теоретичним матеріалом. Це можна зробити тут i тут.

Задача 1: Перпендикуляр проведений з вершини прямокутника на діагональ, дорівнює «12» і поділяє діагональ на відрізки, різниця яких дорівнює «7». Знайти площу прямокутника.

Намалюємо прямокутник «ABCD», проведемо діагональ «AC» та перпендикуляр до неї «ВН».

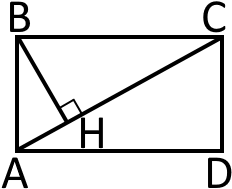
Припустимо, що відрізок «СН» буде більшим за відрізок «АН». Тому: «СН – АН = 7». Якщо ми позначимо довжину відрізка «АН» як «х», тобто «АН = х», тоді відрізок «СН» буде мати довжину «СН – х = 7», звідси отримаємо: «СН = х + 7».

Оскільки діагональ прямокутника ділить його на два рівні прямокутні трикутники («ABC» та «ADC»), то площу прямокутника ми зможемо знайти як суму площ цих двох трикутників, але врахувавши, що вони однакові, то достатньо знайти один з них та помножити на «2».

Тобто, площу прямокутника «АВСD» можна знайти так:

S_ABCD = 2S_ABC

Розглянемо трикутник «АВС». У ньому кут «В» є прямим, «АС» - гіпотенуза, «ВН» - висота, що проведена до гіпотенузи. Оскільки, ми маємо висоту «ВН», то площу можна буде знайти за формулою:

S = /1/2 AC ∙ BH

Нам необхідно лише знайти «АС». Врахувавши, що ми маємо висоту «ВН» проведену до гіпотенузи та маємо відрізки «АН» і «СН», то можна скористатися співвідношенням у прямокутному трикутнику:

BH² = AH ∙ CH

Підставимо наші значення:

12² ⁡⁡= x(x + 7)

x(x + 7) = 144

Розв’яжемо отримане рівняння:

x²⁡ ⁡+ 7x - 144 = 0

D = 7² ⁡⁡- 4∙1∙(-144) = 49 + 576 = 625

x₁⁡⁡ = /-7 + √625/2 ∙ 1 = 9

x₂⁡⁡ = /-7 - √625/2 ∙ 1 = -16

Оскільки через «х» ми позначали довжину відрізка «АН», то розв’язок «-16» нам не підходить, бо довжина не може бути від’ємною.

Матимемо, що довжина «АН = 9», а «СН = 9 + 7 = 16». Тоді довжина «АС» буде:

АС = АН + СН

АС = 9 + 16 = 25

Отже, ми вже маємо всі данні для знаходження площі трикутника. А це означає, що можна відразу шукати площу прямокутника.

S_ABCD⁡⁡ = 2S_ABC⁡⁡

S_ABCD⁡⁡ = 2 ∙ /1/2 ∙ AC ∙ BH

S_ABCD ⁡⁡= AC ∙ BH

S_ABCD⁡⁡ = 12 ∙ 25

S_ABCD⁡⁡ = 300

Відповідь: 300.

Задача 2: Одна з діагоналей паралелограма дорівнює «6√6» і утворює зі стороною паралелограма кут «60» градусів. Знайти іншу діагональ, якщо вона утворює з тією ж стороною кут «45» градусів.

Намалюємо паралелограм «АВСD» та проведемо у ньому діагоналі «АС», «ВD», а точку перетину діагоналей позначимо «О».

Припустимо, що діагональ «ВD» утворює кут «60» градусів із стороною «АD» в такому випадку «ВD = 6√6», тоді діагональ «АС» буде утворювати кут «45» градусів із стороною «АD» (за умовою задачі).

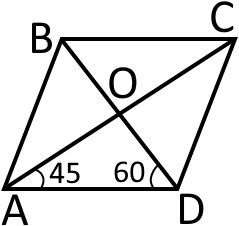
Діагоналі прямокутника в точці перетину діляться навпіл. Тому «АО = СО = /AC/2» і «BO = DO = /BD/2».

Врахувавши це нам достатньо знайти довжину відрізка «BO» або «DO» після чого можна знайти довжину «BD».

Розглянемо трикутник «АOD». У ньому сторона «DО = /BD/2 = /6√6/2 = 3√6», а «AO = х».

Для того щоб знайти сторону «AO» скористаємося теоремою синусів. Будемо мати:

/AO/sin⁡ ODA = /DO/sin⁡ OAD

Звідси знайдемо «AO»:

AO = DO∙sin⁡ODA∶sin⁡OAD

Підставимо наші данні:

AO = 3√6 ∙ /√3/2 ∶ /√2/2

AO = 9

Тоді діагональ «AC» буде:

AC = 2AO = 2 ∙ 9 = 18

Відповідь: 18.

Задача 3: Одна з діагоналей трапеції, яка дорівнює «3√6», утворює з основою трапеції кут «60» градусів. Обчислити довжину другої діагоналі, якщо вона утворює з тією ж основою кут «45» градусів.

Намалюємо трапецію «ABCD» та проведемо діагоналі «AC» та «BD». Також проведемо висоти «ВН» і «СМ» до основи «AD».

Припустимо, що діагональ «BD» має кут з основою «AD» «45» градусів («∠ADB= 45»). Тоді діагональ «АС» буде мати кут з основою «AD» «60» градусів («∠CAD = 60»). Тоді довжина діагоналі «АС» буде «3√6».

Після того як ми провели висоти «ВН» та «СМ» та діагоналі «BD» та «АС», то отримали два прямокутні трикутники «АМС» та «ВНD».

В цих трикутниках діагоналі будуть як гіпотенузи. А висоти будуть як катети. Враховуючи, що вони є однаковими, то ми можемо знайти висоту з трикутника «АМС» та використати це у трикутнику «DHB». Розглянемо трикутник «АМС».

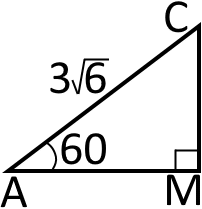
Для того щоб знайти сторону «СМ» скористаємося синусом кута «А». Будемо мати:

sin⁡ A = /CM/AC

Звідси можемо знайти довжину «СМ»:

CM = AC · sin ⁡A

CM = 3√6 ∙ /√3/2

CM = /9√2/2

Оскільки нам відома висота «ВН = СМ», то ми можемо знайти довжину «BD» з трикутника «BHD».

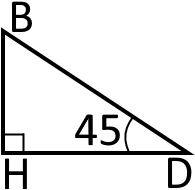
Для того щоб знайти сторону «BD» ми можемо скористатися синусом кута «D».

sin⁡ D = /BH/BD

BD = BH ∶ sin ⁡D

BD = /9√2/2 ∶ /√2/2

BD = 9

Відповідь: 9.

Задача 4: Висоти паралелограма дорівнюють «4» і «6», а його периметр — «40». Знайти: площу паралелограма.

Намалюємо паралелограм «ABCD» та проведемо висоту «BH» до сторони «AD» та висоту «BM» до сторони «CD».

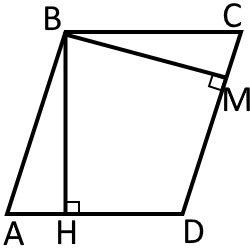
Припустимо, що висота «ВН» дорівнює «4», а висота «ВМ» буде «6». Врахувавши, що ми маємо паралелограм, а у нього протилежні сторони рівні. Тобто: «АВ = CD», «BC = AD». Позначимо «BC» та «AD» через «х». Тоді сторони «АВ», «CD» можна знайти через периметр.

AB+BC+CD+AD = P

Врахувавши, що «АВ = CD», «BC = AD = х», матимемо:

AB + x + AB + x = 40

2AB + 2x = 40

AB + x = 20

AB = 20 - x

Площу ромба ми можемо знайти помноживши сторону ромба на висоту яка проведена до неї. Враховуючи це ми будемо мати такі формули:

S = AD ∙ BH; i S = CD ∙ BM

Оскільки ліві частини в обох формулах однакові, то це означає, що праві частини також однакові:

AD ∙ BH = CD ∙ BM

Підставивши всі данні матимемо:

4x = 6(20 - x)

Розв’яжемо отримане рівняння:

4x = 120 - 6x

4x + 6x = 120

10x = 120

x = 120 ∶ 10

x = 12

Тепер ми можемо знайти довжину сторін паралелепіпеда.

BC = AD = 12

АВ = CD = 20 – 12 = 8

Тепер ми можемо знайти площу:

S = AD ∙ BH

S = 8 ∙ 6

S = 48

Відповідь: 48.

Задача 5: Одна сторона паралелограма на «2» більша за іншу, а його діагоналі дорівнюють «8» і «14». Знайти периметр паралелограма.

В паралелограмі матимемо дві сторони «a», «b» та дві діагоналі «d₁⁡⁡» і «d₂⁡⁡». Отже, позначимо через «х» довжину першої сторони «а = х» і через «х + 2» довжину другої сторони «b = x + 2»; а довжини діагоналей будуть «d₁⁡⁡ = 8» і «d₂⁡⁡ = 14».

Оскільки, сторони паралелограма ми переписали через одну змінну, то ми можемо скористатися властивістю паралелограма:

2a² ⁡⁡+ 2b² ⁡⁡= d/1/2 + d/2/2

Підставимо наші значення:

2x²⁡⁡ + 2(x + 2)²⁡ ⁡= 8² ⁡⁡+ 14²⁡⁡

2x² ⁡⁡+ 2(x²⁡ ⁡+ 4x + 4) = 64 + 196

2x²⁡⁡ + 2x² ⁡⁡+ 8x + 8 = 260

4x²⁡⁡ + 8x + 8 - 260 = 0

4x²⁡⁡ + 8x - 252 = 0 |∶4

x²⁡⁡ + 2x - 63 = 0

D = 2² ⁡⁡- 4∙1∙(-63) = 4 + 252 = 256

x₁ ⁡⁡= /-2 + √256/2 ∙ 1 = 7

x₂⁡ ⁡= /-2 - √256/2 ∙ 1 = -9

Оскільки, через «х» ми позначали довжину сторони «а», а довжина не може бути від’ємною тому ми маємо відкинути значення «х = -9».

Довжина сторони «а» буде «а = 7», довжина сторони «b» буде «b = 7 + 2 = 9». Тепер ми можемо знайти периметр:

P = 2(a + b)

P = 2(7 + 9)

P = 32

Відповідь: 32.

Задача 6: Основи трапеції дорівнюють «10» і «24», а бічні сторони — «15» і «13». Знайти площу трапеції.

Намалюємо трапецію «ABCD» та проведемо висоти «ВМ» і «СН».

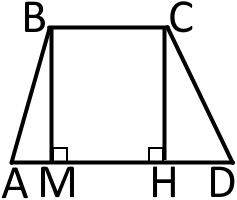
В нашій трапеції «AB = 13», «CD = 15», «BC = 10», «AD = 24». Після того як ми провели висоти «ВМ» і «СН» у нас утворилися трикутники «ABМ» і «CНD» та прямокутник «МВСН».

З прямокутника «МВСН» будемо мати, що «МН = ВС», тому «МН = 10». Тоді довжина «АМ + HD = АD – МН», тому «АМ + НD = 24 - 10», «АМ + НD = 14».

Для того щоб знайти площу трапеції «ABCD». Ми можемо додати площі фігур з яких вона складається.

Ми можемо скласти трикутники «ABМ» і «CНD» в один єдиний. Тоді точки «В» і «С» збігаються також збігаються точки «М» та «Н». Тому ми отримаємо трикутник «ABD».

В нашому трикутнику «ВМ» буде висотою, «АВ = 13», «BD = 15», «AD = 14». Знайдемо площу трикутника «ABD» використавши формулу Герона.

S = p(p-a)(p-b)(p-c)

Де «p» - півпериметр; «a», «b», «c» - сторони трикутника.

Знайдемо півпериметр:

p = /AB+BD+AD/2

p = /13+14+15/2 = 21

Площу нашого трикутника можемо знайти так:

S_∆ = p(p-AB)(p-BD)(p-AD)

S_∆ = 21(21-13)(21-15)(21-14) = 84

Для того щоб знайти площу прямокутника «МВСН» необхідно знайти довжину сторони «ВМ» чи «СН». А сторона «ВМ» є висотою трикутника «ABD». Скористаємося формулою пошуку площі трикутника за допомогою висоти.

S_∆ = /AD ∙ BM/2

Звідси ми можемо знайти довжину «ВМ».

BM = /2S_∆/AD

BM = /2 ∙ 84/14

BM = 12

Знайдемо площу прямокутника «МВСН».

S_⊡ = BC ∙ BM

S_⊡ = 10 ∙ 12

S_⊡ = 120

Тепер знайдемо площу трапеції «ABCD» додавши площі трикутника «ABD» та прямокутника «MBCH».

S = S_∆ + S_⊡

S = 84 + 120

S = 204

Відповідь: 204.

Задача 7: Висота ромба дорівнює «24», а менша діагональ – «30». Знайти більшу діагональ ромба.

Намалюємо ромб «ABCD» та проведемо діагоналі «AC» і «BD». Також проведемо діагональ «МН», що буде проходити через точку перетину діагоналей «О».

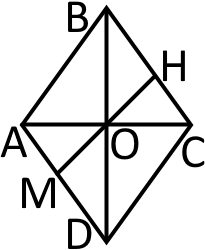
В нашому ромбові «АС = 30», «МН = 24». Розглянемо трикутник «ВОС», де «OH = /MH/2 = /24/2 = 12» - висота проведена до гіпотенузи «ВС», «OС = /АС/2 = /30/2 = 15» - катет. Якщо ми знайдемо відрізок «ВО», то зможемо знайти всю довжину «BD», бо «BD = 2ВО».

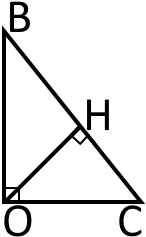
З прямокутного трикутника «ОНС» за теоремою Піфагора знайдемо довжину «СН».

CH²⁡⁡ = OC² ⁡⁡- OH²⁡⁡

CH²⁡⁡ = 15²⁡ ⁡- 12²⁡⁡

CH²⁡⁡ = 225 - 144

CH²⁡⁡ = 81

CH = √81

CH = 9

Після чого за співвідношеннями у прямокутному трикутнику можемо знайти довжину сторони «ВС».

OC² ⁡⁡= CH ∙ CB

CB = OC²⁡⁡CH

CB = 15²9⁡⁡ = 25

Після за теоремою Піфагора ми зможемо знайти довжину відрізка «ВО».

BO²⁡⁡ = BC²⁡ ⁡- OC²⁡⁡

BO²⁡⁡ = 25² - 15²

BO²⁡⁡ = 625 - 225

BO²⁡⁡ = 400

BO = √400

BO = 20

Оскільки, нам відома довжина «ВО», то ми можемо знайти довжину всієї діагоналі «BD».

BD = 2BO

BD = 2∙20 = 40

Відповідь: 40.