Піраміда. Основні поняття та елементи

Піраміда це багатогранник одна грань якого є багатокутником цю грань називають «основою піраміди», а всі інші гранні є трикутниками зі спільною вершиною.

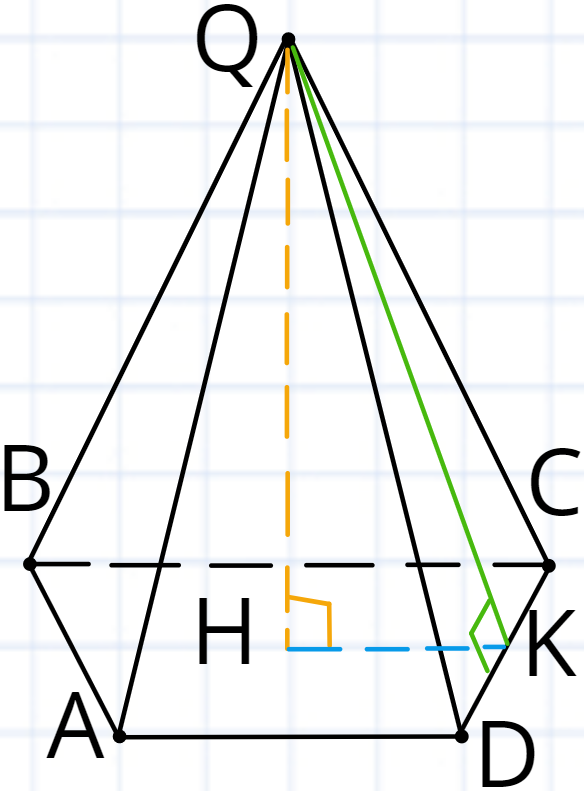
Розглянемо піраміду «QABCD», де «Q» є «вершиною піраміди», а багатокутник «ABCD» є «основою піраміди».

Грані «AQB», «BQC», «CQD», «AQD» називають «бічними гранями піраміди».

Сторони бічних граней, які не належать основі «QA», «QB», «QC», «QD» називають «бічними ребрами».

Перпендикуляр проведений з вершини піраміди до її основи «QH» називають «висотою піраміди». При цьому точку «Н» називають «основою висоти».

Перпендикуляр проведений з вершини піраміди до сторони основи «QK» називають «висотою бічної грані». А, точку «К» називають «основою висоти бічної грані».

Піраміду називають «n-кутною», якщо в її основі знаходиться «n-кутник». Наприклад, якщо розглянути піраміду «QABCD», то вона є чотирикутною, бо в її основі знаходиться чотирикутник «ABCD».

Правильна піраміда. Піраміду називають «правильною», якщо в її основі знаходиться правильний багатокутник.

Висоту правильної піраміди також ще називають «віссю піраміди», а висоту бічної грані правильної піраміди називають «апофемою».

У правильної піраміди всі бічні ребра рівні між собою. Відповідно, бічні грані є рівними рівнобедреними трикутниками.

Доволі часто навколо основи піраміди можна описати або вписати коло. При певних умовах ми можемо дізнатися де буде знаходитися центр даного кола.

Коло вписане в основу піраміди. Якщо виконується одна з умов:

То, центр вписаного кола буде збігатися з основою висоти піраміди. «Н» - є основою висоти піраміди і центром вписаного кола.

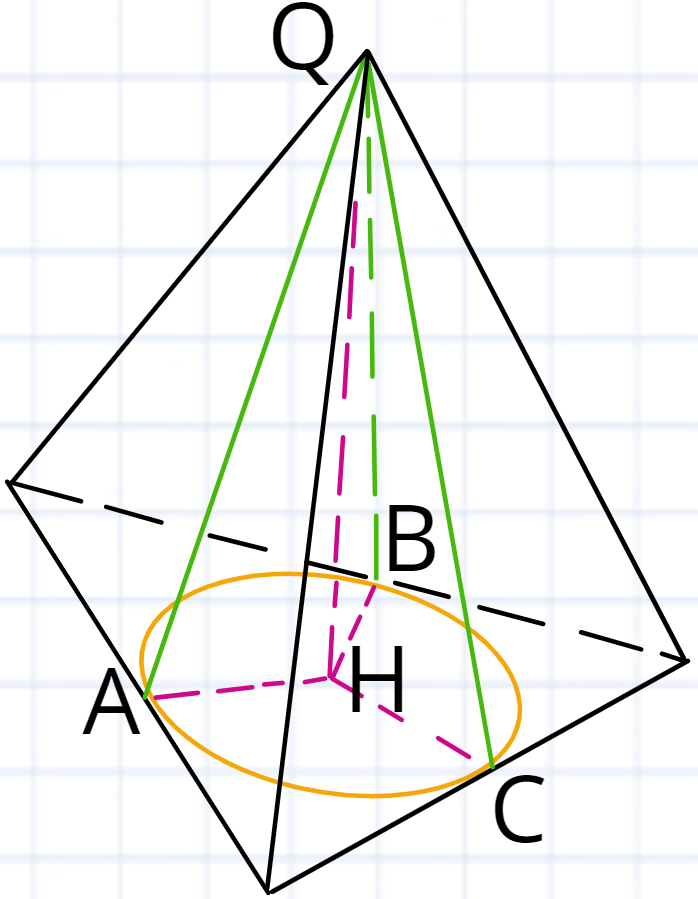
Коло описане навколо основи піраміди. Якщо виконується одна з умов:

То, центр описаного кола буде збігатися з основою висоти піраміди. «Н» - є основою висоти піраміди і центром описаного кола.

Переріз піраміди

У піраміді може бути велика різноманітність перерізів. І всі вони будуть мати як різне розташування так і форму. Можна виділити хіба що два перерізи.

«Діагональний переріз» це переріз який проходить через діагональ основи піраміди. Також, можна сказати, що це переріз який проходить через два бічних ребра які не належать одній грані.

Також може бути переріз який є перпендикулярним до висоти піраміди (або можна сказати, що він є паралельним до основи піраміди). В такому випадку ми отримаємо подібну фігуру до основи піраміди (такої ж форми але меншого розміру) і зможемо скористатися властивостями подібних фігур.

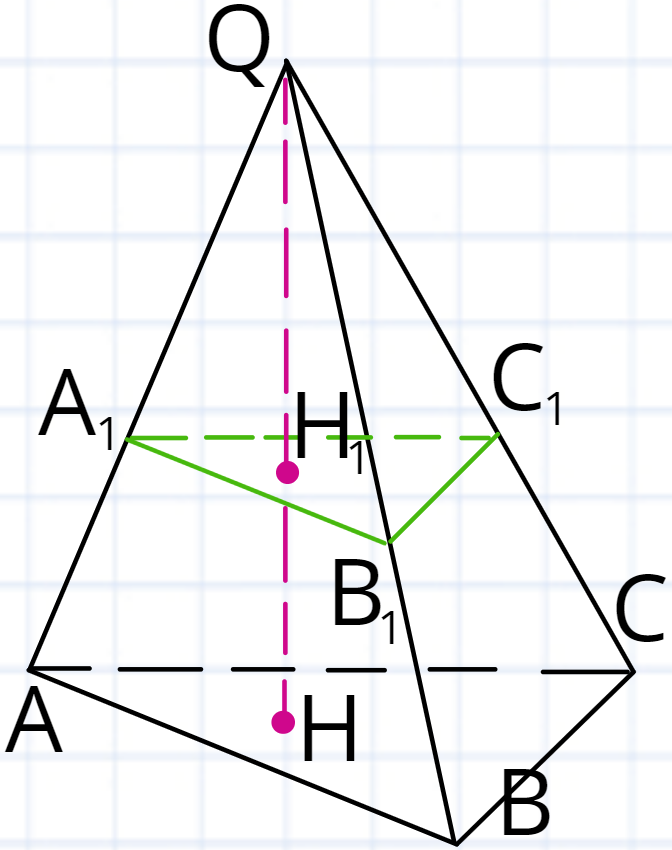
У такому випадку ви будете мати не лише подібні переріз та основу піраміди, а і подібні піраміди.

Відповідно, піраміди «QABC» та «QA₁B₁C₁» є між собою подібними та в них виконуватимуться властивості подібних фігур:

QA₁QA = ⋯ = A₁B₁AB = ⋯ = QH₁QH = ⋯ = S_A1B1C1S_ABC = k

S_A1B1C1S_ABC = k²

І так далі.

Площі піраміди

У піраміди виділяють три основні типи площі.

«Площу основи піраміди» записують як «S_о». Площа основи піраміди буде залежати від багатокутника який буде знаходитися в основі.

«Площу бічної поверхні» (бічна поверхня піраміди) записують як «S_б». Площа бічної поверхні піраміди буде рівна сумі площ бічних граней.

S_б = S₁ + S₂ + ⋯ + S_n

Якщо, ви маєте правильну піраміду, то площу бічної поверхні можна знайти як «добуток півпериметру основи та апофеми».

S_б = /1/2P_оl = pl

Де «P_о» - периметр основи (або «p» - півпериметр основи) та «l» - апофема (висота бічної грані правильної піраміди).

«Площу повної поверхні піраміди» (повна поверхня піраміди) записують як «S_п». Площа повної поверхні піраміди буде рівна сумі площ бічної поверхні та основи.

S_п = S_б + S_о

Об’єм піраміди

Об’єм зазвичай позначають як «V» і він буде рівний третині добутку площі основи та висоти піраміди.

V = /1/3S_оh

Де «S_о» - площа основи піраміди, «h» - висота піраміди.