Призма. Елементи призми. Види призми

В першу чергу варто розібратися що таке призма.

Призма – це багатогранник дві грані якого є рівними та паралельними між собою багатокутниками, а їх відповідні сторони є паралельними (ці грані називають «основами» призми), а інші грані є паралелограмами (та різновидами паралелограму: квадрат, прямокутник, ромб). Ці грані називають «бічними».

З призмою ви зустрічаєтеся кожного дня. Основна маса кімнат є призмами. Книги, зошити, мобільні телефони, ноутбуки мають схожу форму до призми.

Призму називають «n-кутною», якщо в її основі знаходиться «n-кутник».

Давайте намалюємо чотирикутну призму та розглянемо її елементи.

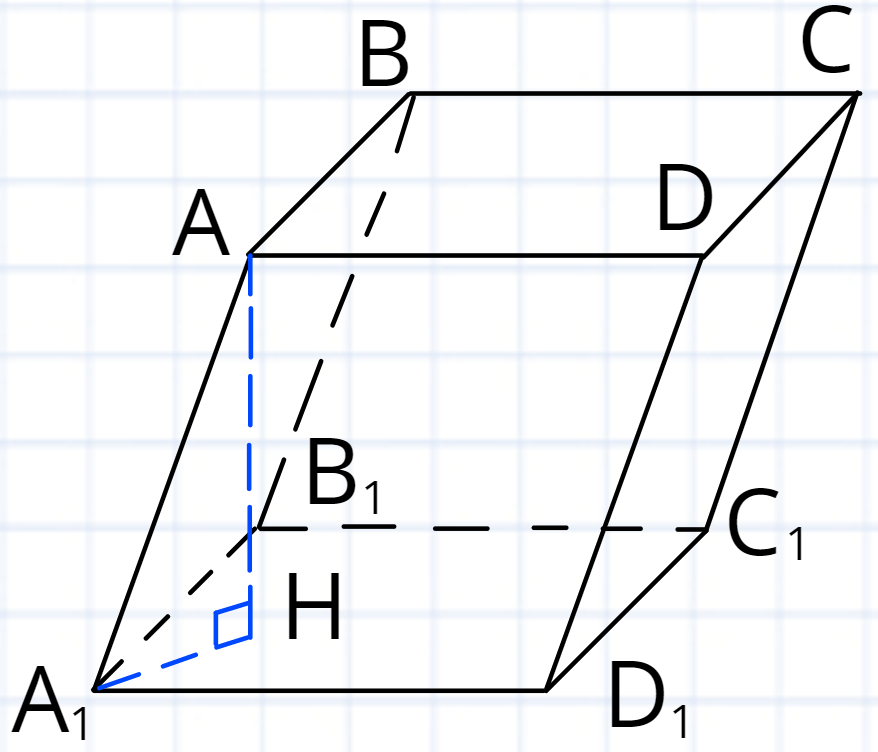
Кажуть, що це призма «ABCDA₁B₁C₁D₁», де «ABCD» та «A₁B₁C₁D₁» «основи призми». А, всі інші грані є «бічними гранями призми».

Відрізок який є перпендикулярним до основ призми називають «висотою призми» (наприклад: «АН»). Зазвичай висоту призми малюють з вершини однієї основи перпендикулярно до площини іншої основи.

Сторони призми називають «ребрами». Но, сторони які належать основам призми часто називають «сторонами основи» (для прикладу «АВ», «ВС»), а сторони бічних граней які не належать основам називають «бічними ребрами» (наприклад: «AA₁», «BB₁» - бічні ребра).

Призма може мати до трьох типів діагоналей (пам’ятаємо, що діагональ це відрізок, який з’єднує не сусідні вершини):

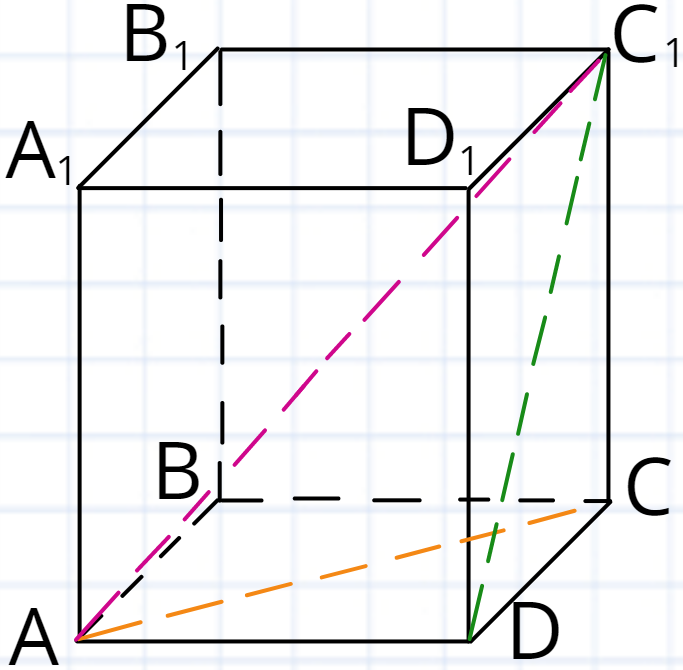
Для прикладу «AC» є діагоналлю основи, «DC₁» - діагональ бічної грані, «AC₁» - діагональ призми.

Зауважимо, що у трикутній призмі буде лише діагональ бічної грані.

Якщо бічні грані є перпендикулярними до основ, то таку призму називають «прямою». У такої призми бічне ребро буде також висотою призми.

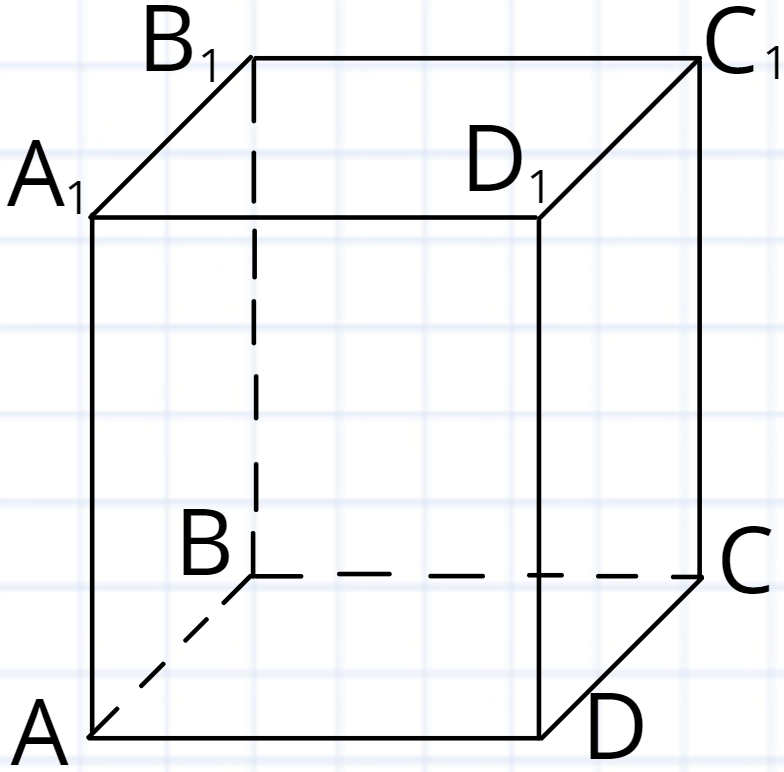
Якщо бічні грані призми є нахиленими до основ, то таку призму називають «похилою».

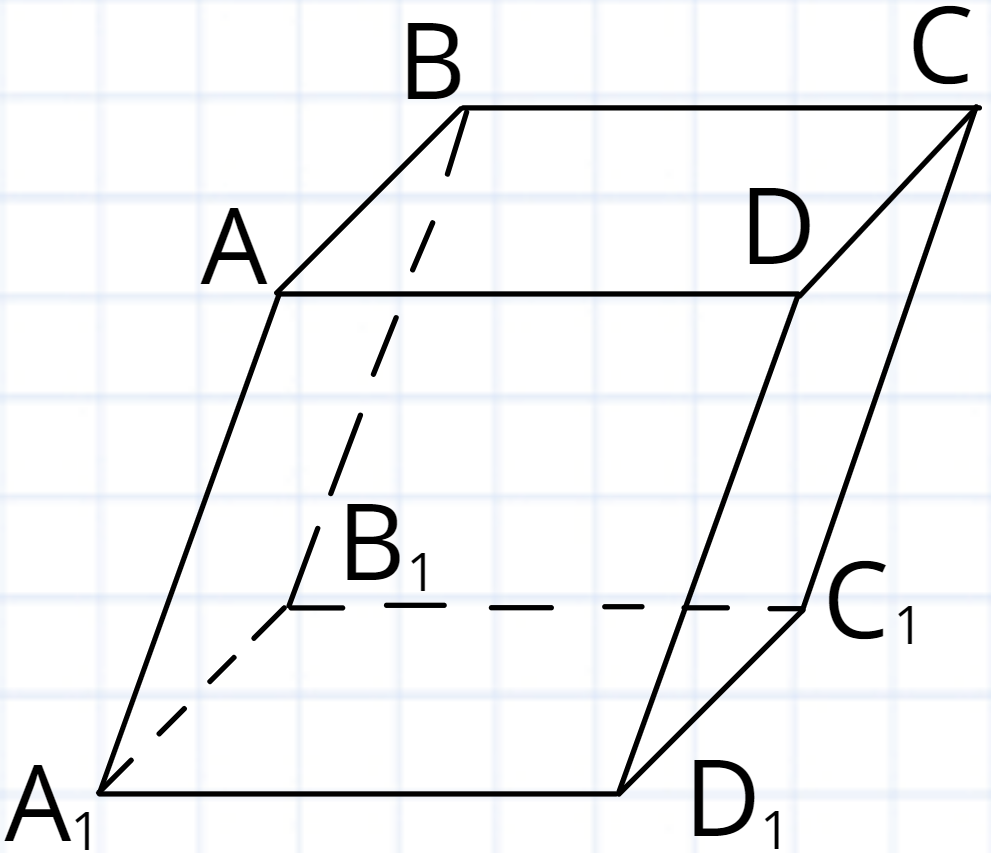
Призма в основі якої знаходиться правильний багатокутник (правильний багатокутник це багатокутник у якого всі сторони рівні між собою і всі внутрішні кути рівні між собою) називається «правильною».

Перерізи призми

Уявіть тортик. Припустимо, що цей тортик є нашою призмою. Якщо взяти ніж та почати розрізати тортик, то ви можете розділити його на дві частини. При цьому розріз який утворився буде «перерізом». Відповідно, цей тортик ви можете розрізати великою кількістю способами. Аналогічно, може бути велика кількість різнотипних перерізів призми.

Переріз який проходить через два бічних ребра які не належать одній бічній грані (переріз проходить через діагональ призми і перпендикулярно до основ призми) називається «діагональним».

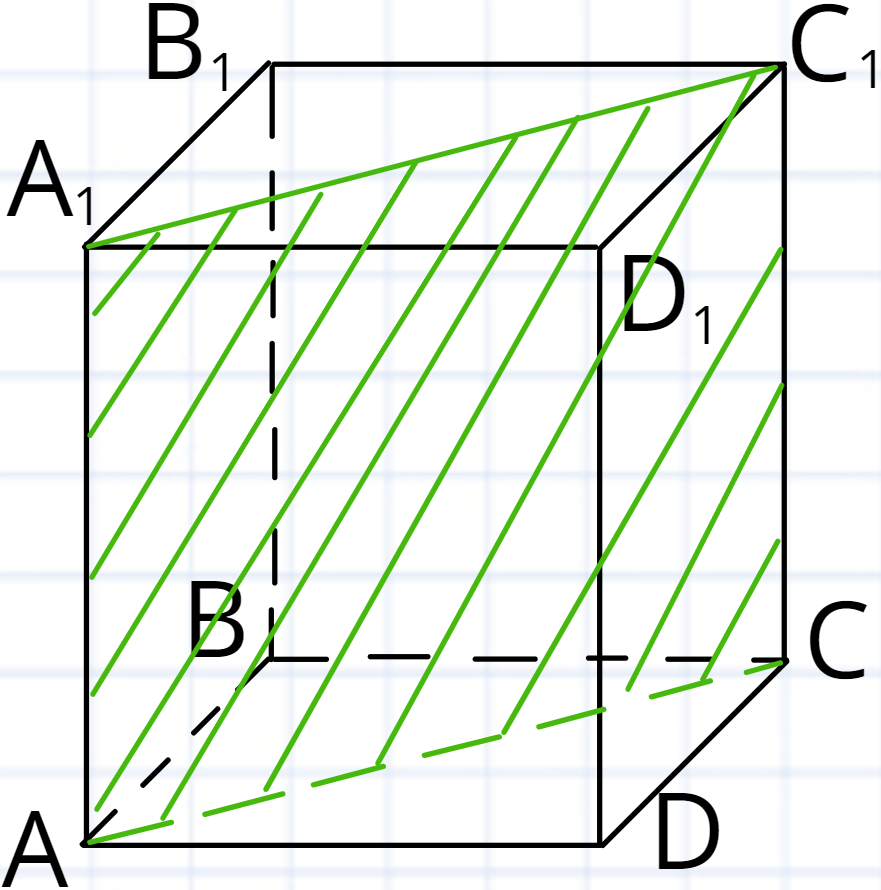
Це по факту єдиний переріз який має свою назву. В інших випадках будуть просто вказувати через яку площину проходить цей переріз.

Зауважимо, що часто використовують такі вирази «переріз проходить через площину «ABC₁»». Хоча трьома літерами позначають трикутники, но в даній ситуації так показують три точки через які проходить площина перерізу!

Для прикладу, візьмемо пряму чотирикутну призму «ABCDA₁B₁C₁D₁» та проведемо у ній переріз «CDB₁».

Як бачите, хоча переріз названий як трикутник, но в результаті ми маємо прямокутник (дуже часто отримуватимемо різновиди паралелограма).

Якщо ваш переріз буде паралельним до основ трапеції, то переріз буде таким же як і основа трапеції (тобто, ми отримаємо фігуру яка буде рівна основі трапеції).

Для прикладу візьмемо трикутну призму та проведемо в ній переріз «МНК» який буде паралельним до основи призми.

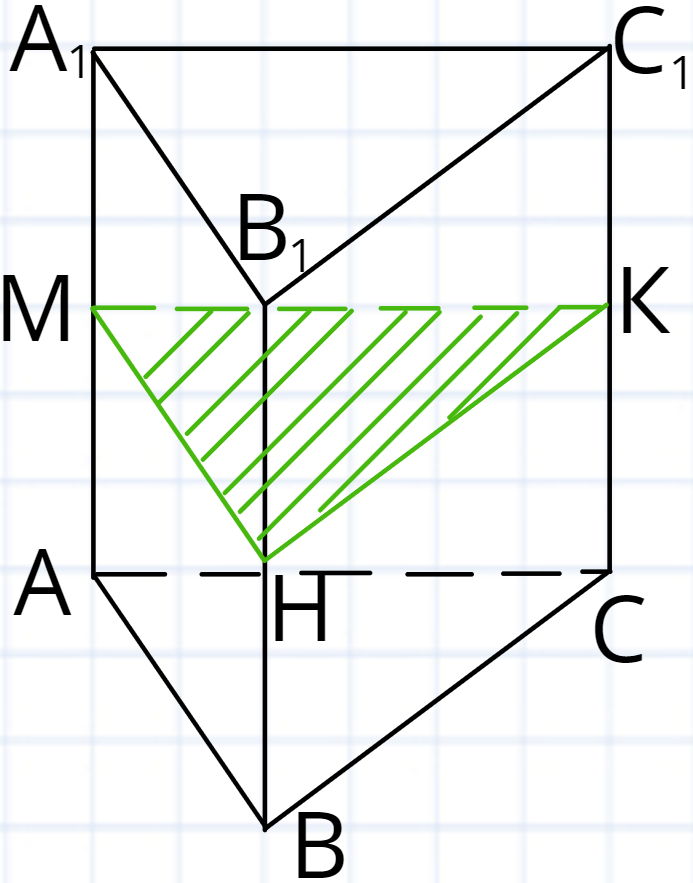
В такому випадку ми отримаємо, що фігура основи (трикутник «АВС») та фігура яка утворилася при перерізі (трикутник «МНК») будуть між собою рівними «Δ АВС = Δ МНК».

Площа призми

У призмі (і в багатьох об’ємних фігурах) виділяють три різновиди площі.

Площа основи. Це площа фігури яка знаходиться в основі призми. Площу основи часто позначають як «S_o».

Площа бічної поверхні. Це сума площ всіх бічних граней призми. Також, площу бічної поверхні називають ще бічною поверхнею. В задачах це може звучати приблизно так: «бічна поверхня призми дорівнює «20 см²»…» при цьому ви маєте усвідомлювати, що мова йде про площу бічної поверхні. Площу бічної поверхні часто позначають як «S_б».

Площу бічної поверхні можна знайти як суму площ бічних граней:

S_б = S₁ + S₂ + ⋯ + S_n

Де «S₁», «S₂», …, «S_n» - площі кожної бічної грані.

Розглянемо прямокутну пряму. Візьмемо для прикладу трикутну призму (в ній просто менше писати ).

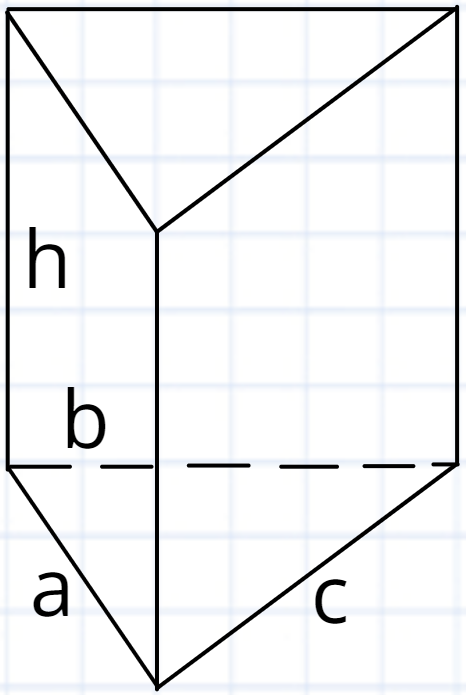
Напишемо для цієї призми площу бічної поверхні.

S_б = S₁ + S₂ + S₃

Враховуючи, що «S₁», «S₂», «S₃» площі бічних граней, то ми можемо їх розписати: «S₁ = ah», «S₂ = bh», «S₃ = ch».

Давайте підставимо ці записи у формулу площі бічної поверхні:

S_б = ah + bh + ch

Зверніть увагу, ми маємо в кожному доданку «h». Винесемо його за дужки:

S_б = (a + b + c)h

У дужках ми отримали суму сторін основи «a + b + c», а якщо пригадати, то суму всіх сторін фігури називають периметром. Тому, запис «a + b + c» ми можемо замінити на периметр основи (позначимо його як «P_o»).

Отже, площу бічної поверхні прямої призми можна записати як периметр основи помножити на висоту:

S_б = P_o ∙ h

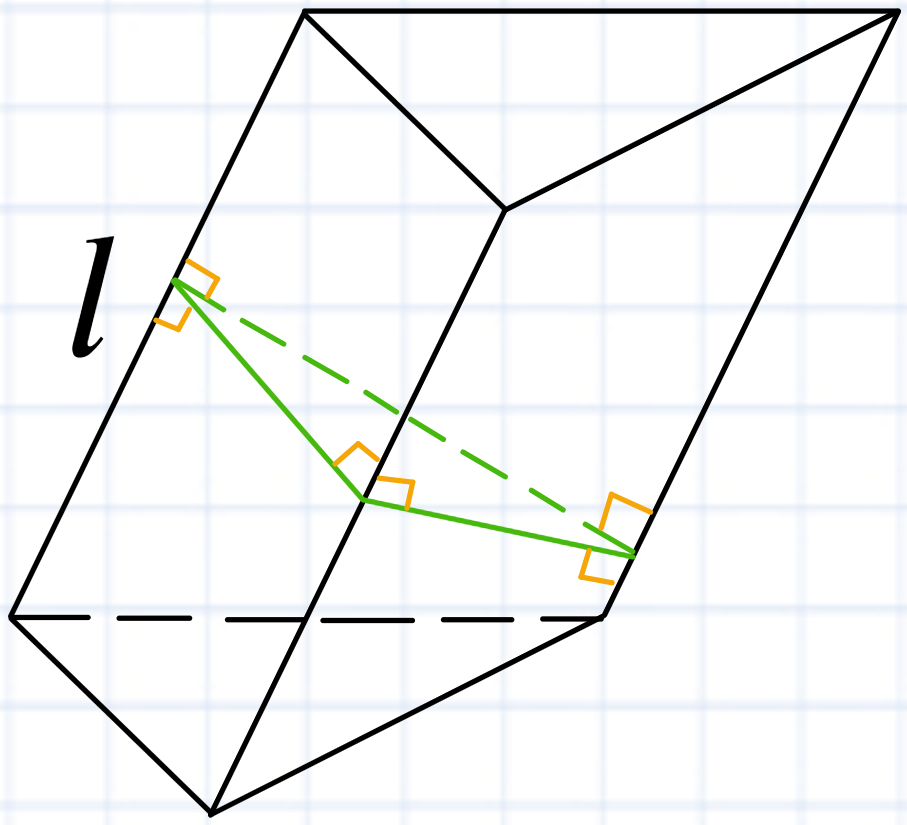
Якщо ви маєте похилу призму, то площу бічної поверхні можна знайти як периметр перерізу який є перпендикулярним до бічних ребр («P_{пер.перер}») помножити на довжину бічного ребра («l»).

S_б = P_{пер.перер} ∙ l

Площа повної поверхні. Це сума площі бічної поверхні та двох площ основи (бо є верхня та нижня основа). Площу повної поверхні також ще називають повною поверхнею. Площу повної поверхні часто позначають як «S_п».

S_п = S_б + 2S_о

Об’єм призми

З об’ємом ви дуже часто зустрічаєтеся в реальному житті. Наприклад, коли купуєте воду, то ви можете обирати по кількості води «1 л.», «1,5 л.», «2 л.» і так далі. Саме ці числа вказують на об’єм. Грубо кажучи об’єм це кількість літрів води яка може поміститися в щось (пляшку, чашку, тарілку і тд).

Об’єм позначають як «V».

І ні. В даному випадку «V» не означає «Vendetta»

Для того щоб знайти об’єм призми, вам необхідно помножити площу основи на висоту призми:

V = S_o · h

Маленька халява на майбутнє. Об’єм майже у всіх фігурах (сфери шукають за іншим принципом) буде знаходитися за однією і тією ж формулою «V = S_oh». Але у фігурах де з верху знаходиться «гостряк» буде записуватися ще «/1/3». Тобто, формула буде такою: «V = /1/3 S_oh».

Особливі види призми. Куб. Паралелепіпед

Деколи розглядають такі види призми як «Куб» та «Паралелепіпед». Вони мають всі властивості призми але для них зробили вже «готові» формули. Розглянемо їх.

Куб. Куб це пряма призма всі ребра якої є рівними між собою, тобто кожна грань кубу є рівними квадратами.

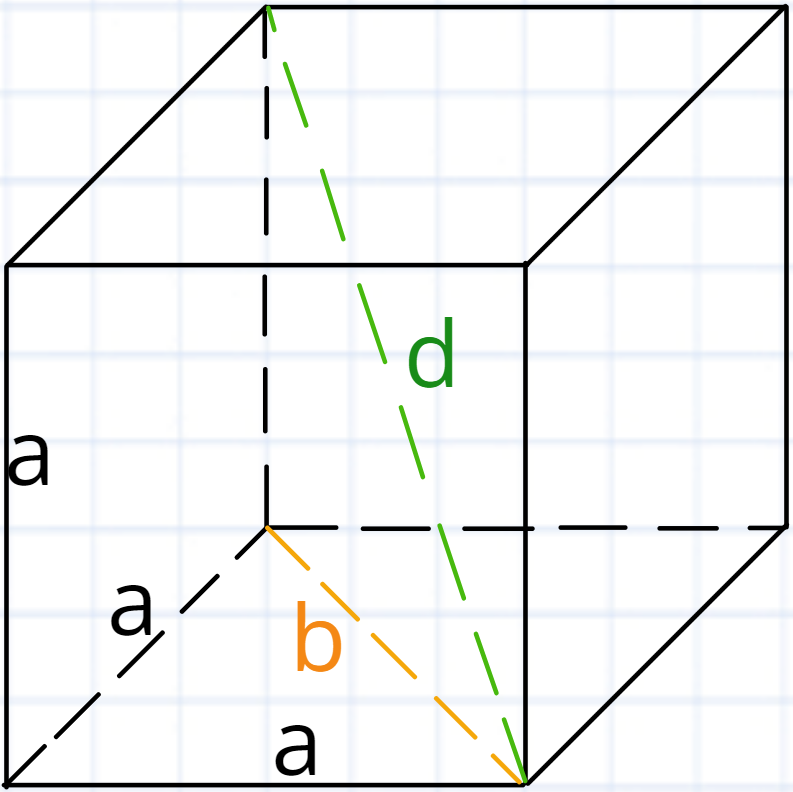
При цьому є не велика халява. Діагональ бічної грані («b») буде рівна стороні помноженій на «√2», тобто «b = a√2». А, діагональ кубу («d») буде рівна стороні помноженій на «√3», тобто «d = a√3».

Враховуючи, що всі грані кубу є однаковими квадратами, то площу повної поверхні можна знайти так:

S_п = 6a²

А, об’єм кубу можна знайти за формулою:

V = a³

Паралелепіпед. Паралелепіпед це призма в основі якої знаходиться паралелограм.

Властивості паралелепіпеда:

Якщо бічні ребра (чи грані) є перпендикулярними до площини основи, то такий паралелепіпед називають «прямим».

У таких випадках бічними гранями будуть квадрати або прямокутники.

На справді малюнки призми будуть майже завжди схожими між собою. Тому, не потрібно дивуватися. Будь-то куб, паралелепіпед чи чотирикутна призма їх дуже часто малюють однаково.

Якщо ж бічні ребра є не перпендикулярними до площини основи, то такий паралелепіпед називають «похилим».

Бічними гранями похилого паралелепіпеда будуть паралелограми або ромби.

Прямокутний паралелепіпед. Це прямий паралелепіпед основою якого є прямокутник.

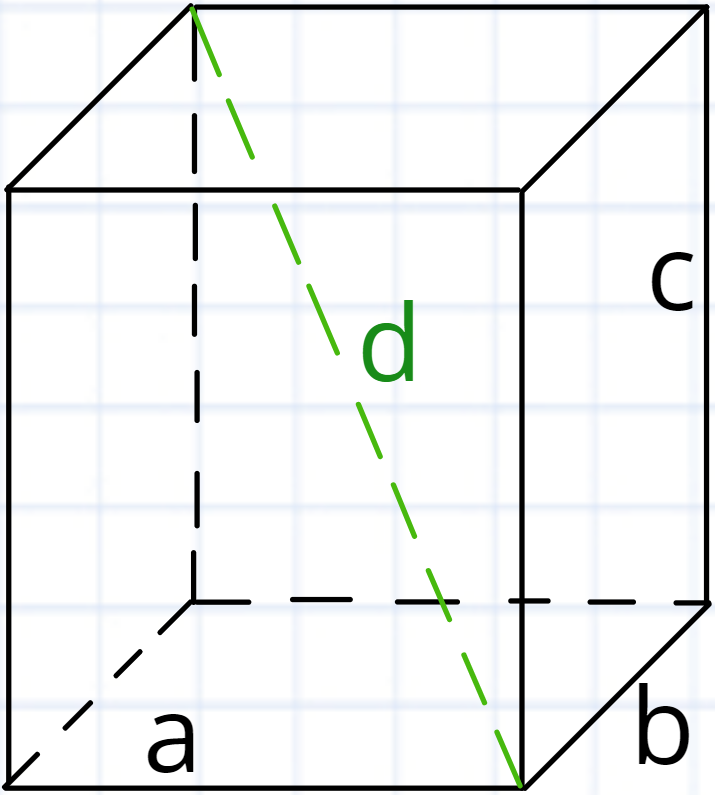
Ми можемо знайти діагональ прямокутного паралелепіпеда за формулою:

d² = a² + b² + c²

Цю формулу можна самостійно отримати за допомогою теореми Піфагора.

Всі чотири діагоналі прямокутного паралелепіпеда є рівними між собою і в точці перетину діляться пополам.

Площу повної поверхні можна знайти за формулою:

S_п = 2(ab + ac + bc)

Об’єм паралелепіпеда можна знайти за формулою:

V = abc

Наголошую. Всі ці формули можна отримати з формул призми. Просто для куба та паралелепіпеда їх вивели (зробили готові) бо ці фігури дуже часто використовуються.