Первісна та інтеграл є доволі схожими поняттями і їх часто не відрізняють. Не хвилюйтеся. В цьому жодної проблеми не має.

Ми вже вивчили похідну функції. Зараз ці знання нам допоможуть. Пригадаємо, що похідну функції «f(x)» позначаємо як «f'(x)».

Ми вивчимо нове поняття первісної функції. Первісну функцію позначають як «f(x)».

Отже, в нас є такі позначення: «f(x)» - функція; «f'(x)» - похідна функції; «F(x)» - первісна функція.

Спробуємо перенести ці поняття у людський світ. Уявіть, що функція це ви. В такому випадку ваші батьки це первісна функція, бо вони були перед вами (як первісні люди). А, ваші діти (майбутні чи наявні) будуть похідною функції, бо походитимуть від вас.

Отже, первісна функція це та функція, що була перед заданою. А, похідна функції це функція, яка буде після заданої.

Тобто, коли ми обчислюємо похідну, то ми знаходимо «дитину» функції. Коли ми обчислюємо первісну, то знаходимо «батьків» функції.

Похідних для функції може бути безліч. Тому, похідна функції може бути загальною, де в кінці ми пишемо константу «C», або конкретною, де константу в кінці не пишемо.

Погляньмо як це працює. Візьмемо для прикладу три функції «x² + 5», «x² - 7», «x²». Та обчислимо похідну кожної функції:

(x² + 5)' = 2x

(x² - 7)' = 2x

(x²)' = 2x

Отже, ми мали три різні функції та знайшли похідну для кожної з них. Зауважте, що всі похідні є однаковими.

Тепер припустимо, що в нас є функція «2x» і нам необхідно знайти її первісну. Але яка з функцій буде первісною? Можливо «x² + 5» або «x² - 7» або «x²» або ще якась інша? На справді всі одночасно. Зауважте, що в кожному з наведених первісних не змінним залишається «x²», а змінюється лише число. Дане число може бути будь-яким «+ 5», «- 7», «0», «- 0,5», «+ /1/3» тощо. Тому, це число заміняють загальною константою «C».

Відповідно, загальний вигляд первісної для функції «2x» буде:

F(x) = x² + C

Замість константи «C» ми записуємо конкретне число лише в тому випадку, коли первісну розглядаємо в конкретній точці. Але про це трішки пізніше.

Для обчислення первісних використовують спеціальні формули та правила й коли ми їх вивчимо, то також будемо користуватися ними. Але, на початку вивчення даної теми у школі вам з великою ймовірністю ніхто не пояснить ці правила/формули. В такому випадку вам на допомогу прийде похідна. Розглянемо приклад такого завдання.

Приклад: чи є функція «F(x) = x¹¹11 - x⁹9 + x²2 + 13x - 7» первісною для функції «f(x) = x¹⁰ - x⁸ + x + 13»?

Враховуючи, що ми не знаємо правил знаходження первісної, тому ми не можемо знайти первісну для функції «f(x)» на пряму. Тобто, ми не можемо довести, що «f(x)» є «батьком» для функції «f(x)». Але ми можемо спробувати довести, що «f(x)» є «дитиною» функції «f(x)». Тобто, ми можемо взяти похідну від функції «f(x)» і перевірити чи вона буде такою ж як функція «f(x)».

(F(x))' = (x¹¹11 - x⁹9 + x²2 + 13x - 7)' = 11x¹⁰11 - 9x9 + /2x/2 + 13 = x¹⁰ - x⁸ + x + 13

Як бачите, похідна від функції «F(x)» є такою ж самою як функція «f(x)», тому «F(x)» є первісною для «f(x)».

Формули обчислення первісної

Формули для обчислення первісної записують за допомогою не визначеного інтеграла. Це виглядає так:

f(x) dx = F(x) + C; C - const

Де «∫» - символ інтеграла, «f(x)» - функція (вираз) від якої обчислюємо первісну, «d» - диференціал, «x» - змінна по якій обчислюється первісна, «F(x)» - первісна.

Варто зауважити, що змінна яка написана під диференціалом є змінною диференціювання. А, будь-яка інша змінна яка записана в інтегралі, але не записана в диференціалі вважається константою (перша формула).

Коли ви маєте не визначений інтеграл, то в результаті первісна буде мати константу «C».

Розглянемо тепер формули для обчислення первісної:

k dx = kx + C; k, C - const

xⁿ dx = x^{n + 1}n + 1 + C; n ≠ -1

Формула степеня використовується дуже часто. Вона необхідна в ситуаціях, коли ми маємо множення/ділення однакових чисел, коли маємо число під коренем.

/1/x dx = ln⁡|x| + C; x ≠ 0

a^x dx = a^xln a + C

Також, дана формула має особливий випадок:

e^x dx = e^x + C

sin⁡ x dx = - cos⁡ x + C

cos ⁡x dx = sin ⁡x + C

1cos²⁡ x dx = tg x + C

1sin² x⁡ dx = - ctg² x + C

tg x dx = - ln⁡|cos ⁡x| + C

ctg x dx = ln⁡|sin⁡ x| + C

Це є основні формули які варто обов’язково знати. Також, напишемо формули для складніших випадків. Вони зазвичай не використовуються в шкільній програмі, але будуть корисні для студентів математичних спеціальностей.

11 - x² dx = arcsin ⁡x + C

1a² - x² dx = arcsin⁡/x/a + C

11 + x² dx = arctg x + C

1a² + x² dx = /1/a arctg/x/a + C

1a² - x² dx = /1/2a ln⁡|/a + x/a - x| + C; a ≠ 0

1x² ± a² dx = ln⁡| x + x² ± a²| + C

xx² ± a² dx = x² ± a² + C

/1/sin ⁡x dx = ln⁡|tg /x/2| + C

/1/cos ⁡x dx = ln⁡|tg (/x/2 + /π/4)| + C

sh x dx = ch x + C

ch x dx = sh x + C

1sh² x dx = - cth x + C

1ch² x dx = th x + C

Дані формули допоможуть вам при обчисленні первісних. Але крім цих формул вам варто також знати правила обчислення первісних.

1. Якщо у вас число множиться на функцію, то це число можна винести за знак інтеграла:

k ∙ f(x) dx = k ∙ f(x) dx = k ∙ F(x) + C

Приклад: обчислити первісну функцію для «3 sin ⁡x».

Напишемо це у вигляді інтеграла: « 3 sin ⁡x dx».

Як бачите, в нас функція множиться на число. Для нашої зручності ми можемо винести це число за межі інтеграла: «3 sin⁡ x dx».

Тепер, ми можемо скористатися формулою для обчислення інтеграла « sin ⁡x dx = - cos ⁡x + C». Матимемо: «3 sin⁡ x dx = 3 ∙ (- cos⁡ x) + C = -3 cos ⁡x + C».

2. Якщо у вас є додавання/віднімання функцій, то ви можете обчислити первісні окремо. Також ми можемо розділити це на різні інтеграли:

[f(x) ± g(x)] dx = f(x) dx ± g(x) dx = F(x) ± G(x) + C

Приклад: обчислити первісну функцію для «x + cos ⁡x - 7».

Напишемо це у вигляді інтеграла: « (x + cos ⁡x - 7) dx».

У випадках, коли ми маємо додавання/віднімання функцій, то ми можемо обчислити первісні окремо. Для цього ви можете розбити ваш інтеграл на окремі частини, хоча це є не обов’язковим кроком. Матимемо: « (x + cos ⁡x - 7) dx = x dx + cos ⁡x dx - 7 dx».

Обчислимо первісні: « x dx + cos ⁡x dx - 7 dx = x²2 + sin ⁡x - 7x + C».

Зауважте, що константа пишеться лише один раз.

3. Якщо у функції змінна множиться на якесь число, то при обчисленні первісної нам варто винести це число перевернувши його:

f(kx + b) dx = /1/k F(kx + b) + C

Приклад: обчислити первісну функцію для «⁡cos/x/4».

Напишемо це за допомогою інтеграла: « cos/x/4 dx».

Скористаємося формулою обчислення первісної. Враховуємо, що «x» ділиться на «4» (пам’ятаємо, що це працює і при множенні), тому потрібно це число винести оберненим. Тобто, ми маємо «/x/4 = /1/4 x». Відповідно «/1/4» нам потрібно перевернути й отримаємо «/4/1 = 4». Матимемо: « cos/⁡x/4 dx = 4 sin⁡/x/4 + C».

Якщо ви маєте множення або ділення функцій, то в такому випадку вам необхідно виконати перетворення, щоб спростити вираз і позбутися від множення/ділення. Схожа ситуація буде при складених функціях. Пізніше ми розглянемо способи, що робити в таких випадках.

Приклад: обчислити первісну «cos²⁡ /x/4».

Дана функція є складеною, оскільки ми маємо степінь та «cos». В таких випадках обчислювати первісну не можна. Потрібно позбутися від складеної функції. Для цього нам необхідно перетворити даний вираз. В цьому допоможуть формули перетворення тригонометричних функцій. В такому випадку: «cos²⁡x = /1 + cos⁡2x/2 = /1/2 + /1/2cos⁡2x».

Матимемо:

cos²⁡ /x/4 dx= (/1/2 + /1/2 cos⁡/2x/4) dx = (/1/2 + /1/2 cos⁡/x/2) dx = /1/2x + /1/2∙ 2 ∙ sin⁡/x/2 + C = /1/2x + sin⁡/x/2 + C

Приклад: обчислити первісну функцію для «sin²⁡ x - 4 cos² ⁡xsin⁡ x - 2 cos ⁡x».

В такому випадку ми маємо ділення функцій. При множенні/діленні функцій первісну функцію обчислювати не можна. Тому, нам необхідно позбутися від множення/ділення.

В чисельнику ми маємо формулу скороченого множення «a² - b² = (a - b)(a + b)». Матимемо:

sin² ⁡x - 4 cos² ⁡x = (sin⁡ x - 2 cos ⁡x)(sin ⁡x + 2 cos ⁡x)

Отже, ми будемо мати:

sin²⁡ x - 4 cos² ⁡xsin⁡ x - 2 cos ⁡x dx = /(sin⁡ x - 2 cos ⁡x)(sin ⁡x + 2 cos⁡ x)/sin ⁡x - 2 cos⁡ x dx = sin⁡ x + 2 cos⁡ x dx

Ми маємо додавання/віднімання функцій. Обчислимо первісну від кожної функції окремо:

sin⁡ x + 2 cos ⁡x dx = - cos ⁡x + 2 sin⁡ x + C = 2 sin ⁡x - cos⁡ x + C

Це є базові речі при обчисленні первісних. Але не завжди вдається скористатися формулами перетворення або формулами скороченого множення.

В такому випадку є правило внесення під диференціал. Тобто, коли ми маємо «dx», то замість «x» можемо написати якусь функцію. Ця функція обирається серед множників/дільників. Коли ми вносимо функцію під диференціал, то потрібно взяти первісну від даної функції. Таким чином в нас мають вийти однакові функції під інтегралом та диференціалом.

Розглянемо все на прикладі: обчислити первісну функцію для «/ln⁡ x/x».

Зауважимо, що вираз «/ln⁡ x/x» можна написати так: «/1/x ∙ ln ⁡x».

Напишемо це за допомогою інтеграла: « /1/x ∙ ln⁡ x dx».

Як бачите, ми маємо множення/ділення функцій. При цьому, ми не можемо позбутися від цього за допомогою перетворень. Хоча ви можете скористатися властивостями логарифма, але в такому випадку ви отримаєте складену функцію, що також нам не підходить.

Але, ми можемо «/1/x» занести під диференціал. Коли ми заносимо вираз під диференціал, то маємо взяти від нього первісну. Тобто, наша функція виглядатиме так:

/1/x ∙ ln⁡ x dx = ln⁡ x d(ln ⁡x)

Тепер, для нашої зручності виконаємо заміну змінної: «ln⁡ x = t». Матимемо:

ln⁡ x d(ln⁡ x) = t dt

Знайдемо первісну:

t dt = /1/2 t² + C

І повернемося до нашої заміни:

/1/2 t² + C = /1/2 ln²⁡ x + C

Це можна записати в такому вигляді:

f(x)∙g(x) dx= f(x) d( g(x)) = f(x) d(f(x))

Даний метод може виглядати по іншому. Вам потрібно одну з функцій записати у вигляді похідної яка в результаті дасть другу функцію. Після чого занести цю похідну в диференціал. В такому випадку похідна зникне. На практиці це виглядатиме так:

[f(x) ∙ g(x)] dx

Записуємо одну з функцій у вигляді похідної яка в результаті дасть іншу функцію. Тобто, ми маємо функцію «g(x)» яку ми напишемо як «[f(x)]'». Маємо:

[f(x) ∙ g(x)] dx = f(x) ∙ [f(x)]' dx

Після чого похідну заносимо під знак диференціала де символ похідної зникає:

f(x) ∙ [f(x)]' dx = f(x) d f(x)

Тепер маючи однакові функції під інтегралом та диференціалом ми можемо виконати заміну змінної та обчислити первісну.

Розгляньмо це на попередньому прикладі: «/1/x ∙ ln ⁡x».

По традиції напишемо це у вигляді інтеграла: « /1/x ∙ ln ⁡x dx».

Тепер нам необхідно визначити яку функцію можна подати у вигляді похідної. Врахуємо, що «(ln⁡ x)' = /1/x». То, в нашому інтегралі можна замінити «/1/x» на «(ln⁡ x)'». Матимемо:

/1/x ∙ ln ⁡x dx = ln ⁡x ∙ (ln ⁡x)' dx

Тепер, нам необхідно «(ln⁡ x)'» занести під диференціал. При цьому знак похідної зникне:

ln ⁡x ∙ (ln ⁡x)' dx = ln ⁡x d(ln ⁡x)

Як бачите, ми отримали однакові вирази під інтегралом та диференціалом. Тепер можна виконати заміну змінної: «ln ⁡x = t». Отримаємо:

ln⁡ x d(ln ⁡x) = t dt

Обчислимо інтеграл:

t dt = /1/2 t² + C

Та повернемося до заміни:

/1/2 t² + C = /1/2 ln²⁡x + C

Як бачите, результати вийшли однаковими.

Інші методи обчислення первісної ми розглянемо пізніше. Оскільки, вони зазвичай використовуються в складних інтегралах.

Інтегрування частинами

Крім того, бувають ситуації, що ми не можемо одну функцію подати через первісну/похідну іншої. В таких випадках приходить на допомогу правило інтегрування частинами:

u dv = uv - v du

Дане правило працює таким чином:

Важливо розуміти, що інтеграл « v du» який ви отримаєте має вийти легшим (або навіть табличним) в порівнянні з початковим інтегралом. Може відбутися таке, що потрібно буде ще раз (а то й декілька разів) скористатися методом інтегрування частинами або іншими способами. Але, якщо ви бачите, що ваш приклад очевидно ускладнився, то потрібно обрати інші функції в якості «u» та «dv».

Наприклад: знайти інтеграл « x · sin⁡ x dx».

Візьмемо в якості «u» функцію «x», а в якості «dv» буде решта, тобто вираз «sin⁡ x dx».

Знайдемо «du» та «v» за описаними вище правилами:

du = (x)' dx = 1 dx = dx

v = sin ⁡x dx = -cos ⁡x

В такому випадку при обчисленні інтегралу ми не записували константу, оскільки в майбутньому будемо мати ще один інтеграл в якому й використаємо константу.

Тепер, спробуємо записати згідно з формулою та перевірити чи отримаємо спрощений інтеграл.

x · sin ⁡x dx = x ∙ (-cos ⁡x) - (-cos ⁡x) dx = -x · cos⁡ x + cos ⁡x dx

Інтеграл « cos⁡ x dx» є табличним, тому ми можемо його дуже легко обчислити.

-x · cos ⁡x + cos⁡ x dx = -x · cos x + sin ⁡x + C

Візьмемо ще один приклад. Знайти інтеграл « x³ · ln ⁡x dx».

Тепер, виберемо свої вирази «u» та «dv». Наприклад, в якості «u» візьмемо «ln⁡ x», а в якості «dv» візьмемо «x³ dx». Відповідно, залишається знайти «du» та «v». Шукатимемо їх за описаними раніше правилами:

du = (ln⁡ x)' dx = /1/x dx

v = x³ dx = #x⁴#4

Об’єднаємо все в один запис:

x³ · ln ⁡x dx = ln ⁡x ∙ #x⁴#4 - #x⁴#4 ∙ /1/x dx = #x⁴ · ln x#4 - /1/4 x³ dx = #x⁴ · ln x#4 - /1/4 ∙ #x⁴#4 + C = #x⁴ · ln x#4 - #x⁴#16 + C

Конкретна первісна

Первісну називають загальною, якщо в ній є константа «C». Але, якщо ми розглядаємо первісну в якійсь конкретній точці, то можна знайти конкретний вигляд первісної. Для цього необхідно буде підставити значення замість аргументу функції - це буде значення точки по координаті «x». Також, потрібно підставити замість первісної – буде значення точки по координаті «y». Після чого залишається знайти значення константи та повторно написати у первісну.

Приклад: для функції «f(x) = sin ⁡x» знайти первісну «f(x)», графік якої проходить через точку «O(0; 2)».

В першу чергу нам варто знайти первісну функцію:

sin⁡ x dx = - cos ⁡x + C

Отже, загальний вигляд первісної такий:

F(x) = - cos ⁡x + C

Тепер, необхідно підставити значення замість аргументу функції та первісної. Зауважимо, що в нас є точка «O». З даної точки ми можемо витягнути таку інформацію: «O(x = 0; F(x) = 2)». Підставимо в первісну дані значення та знайдемо константу «C»:

2 = - cos ⁡0 + C

2 = -1 + C

C = 2 + 1

C = 3

Підставимо отримане значення в загальний вигляд первісної. Тому, матимемо конкретний вигляд первісної:

F(x) = 3 - cos ⁡x

Визначений інтеграл. Властивості та використання

Визначеним інтегралом називають інтеграл в якого вказані межі інтегрування. Визначений інтеграл має вигляд:

a/b f(x) dx

Де «a» та «b» межі інтегрування. При цьому, «a» - нижня межа інтегрування; «b» - верхня межа інтегрування. Все інше залишається без змін.

Для обчислення визначеного інтеграла використовують формулу Ньютона-Лейбница:

a/b f(x) dx = F(x) a/b = F(b) - F(a)

Тобто, вам необхідно знайти первісну функцію. Далі підставити в дану первісну верхню межу інтегрування та відняти значення первісної з нижньою межею інтегрування. Зауважте, що коли ви маєте визначений інтеграл, то константа не з’являється, бо ви отримуєте конкретне значення.

Вертикальна лінія необхідна для того, щоб не забути межі інтегрування.

Приклад: Обчислити: «1/3 (2x - 5) dx».

В першу чергу знаходимо первісну функцію:

1/3 (2x - 5) dx = (2 ∙ x²2 - 5x) 1/3 = (x² - 5x) 1/3

Тепер, підставимо верхню межу та віднімемо нижню межу:

(x²-5x) 1/3 = (3² - 5 ∙ 3) - (1² - 5 ∙ 1) = -6 - (- 4) = -2

Визначений інтеграл має свої властивості:

Межі інтегрування можна поміняти місцями. При цьому, знак інтеграла змінюється на протилежний:

a/b f(x) dx = -b/a f(x) dx

Інтеграл можна розбити на окремі розділивши його за межами:

a/b f(x) dx = a/c f(x) dx + c/b f(x) dx; c ∈ (a; b)

Розділення інтеграла на частини

Вище ми розглянули формулу розбиття інтеграла на частини. ЇЇ зазвичай застосовують, коли функція на заданому проміжку має декілька знаків. Таке, часто буває з модулем. Розглянемо це на прикладі.

Обчислити інтеграл «-1/3x² - 4x + 4 dx».

Варто зауважити, що це є складена функція. Тому, її в першу чергу потрібно спростити. Під коренем ми маємо формулу скороченого множення. Скористаємося нею.

-1/3x² - 4x + 4 dx = -1/3(x - 2)² dx

Зауважимо, що з властивості кореня «a/aⁿ = |a|, n-парне», то будемо мати:

-1/3(x - 2)² dx = -1/3|x - 2| dx

Варто зауважити, що на даному проміжку наша функція буде мати різну поведінку. Якщо «x» буде меншим за «2», то підмодулевий вираз стане від’ємним і модуль розкриється зі знаком мінус (тобто, матимемо «-(x - 2)»). Якщо ж «x» буде більшим «2», то модуль розкриється зі знаком плюс. Саме тому, ми маємо розкрити модуль за його поведінкою та розбити інтеграл:

-1/3|x - 2| dx = -1/2 -(x - 2) dx + 2/3 (x - 2) dx = --1/2 (x - 2) dx + 2/3 (x - 2) dx

Після чого залишається лише обчислити дані інтеграли.

--1/2 (x - 2) dx + 2/3 (x - 2) dx = -(#x²#2 - 2x) -1/2 + (#x²#2 - 2x) 2/3 = -(#2²#2 - 2∙2 - (#(-1)²#2 - 2∙(-1))) + (#3²#2 - 2∙2 - (#2²#2 - 2∙2)) = -(-2 - 2,5) + (0,5 + 2) = 4,5 + 2,5 = 7

Фізичний зміст первісної

Первісну використовують обчислюючи відстань, швидкість, прискорення та час. Розгляньмо позначення які використовують в таких ситуаціях:

«t» - час;

«S(t)» або «X(t)» - відстань/координата це функція яка залежить від часу;

«v(t)» - швидкість це функція яка залежить від часу;

«a(t)» або «W(t)» - прискорення це функція яка залежить від часу;

За допомогою первісної ми можемо написати такі залежності:

S(t) = v(t) dt

v(t) = a(t) dt

В даних ситуаціях використовуються ті ж самі формули первісних, що й у звичайних первісних. Єдине, що замість змінної «x» ми використовуємо «t». Зауважимо, що константа «C» в даних ситуаціях також буде.

Приклад: точка рухається прямолінійно з прискоренням «a(t) = 12t² + 4». Знайти закон руху «S(t)» точки, якщо в момент часу «t = 1 с» її швидкість дорівнювала «10 м/с», а «S(1) = 12 м». У відповідь записати «S(3)».

Для того, щоб обчислити «S(3)» нам необхідно в першу чергу знайти рівняння для «S(t)».

Щоб знайти «S(t)» ми можемо скористатися формулою: «S(t) = v(t) dt». Але, ми не маємо рівняння «v(t)». Для того, щоб знайти рівняння «v(t)» ми можемо скористатися формулою: «v(t)= a(t) dt».

Отже, матимемо такий вигляд первісної:

v(t) = (12t² + 4) dt

Обчислимо первісну:

(12t² + 4) dt = 12 ∙ t³3 + 4t + C = 4t³ + 4t + C

Отже, загальний вигляд функції «v(t)» буде таким:

v(t) = 4t³ + 4t + C

В нашій задачі є таке речення: «в момент часу «t = 1 с» її швидкість дорівнювала «10 м/с»». Ця умова дає можливість знайти значення константи «C». Замість «t» нам варто підставити «1», а замість «v(t)» підставляємо «10». Матимемо:

10 = 4 ∙ 1³ + 4 ∙ 1 + C

10 = 4 + 4 + C

C = 2

Отже, конкретний вигляд функції «v(t)» буде такий:

v(t) = 4t³ + 4t + 2

Тепер, ми можемо знайти загальний вигляд функції «S(t)» за допомогою формули «S(t) = v(t) dt». Матимемо такий вигляд інтеграла:

S(t) = (4t³ + 4t + 2) dt

Обчислимо первісну:

(4t³ + 4t + 2) dt = 4 ∙ t⁴4 + 4 ∙ t²2 + 2t + C = t⁴ + 2t² + 2t + C

Отже, загальний вигляд первісної функції «S(t)» буде таким:

S(t) = t⁴ + 2t² + 2t + C

В умові завдання є таке речення: «S(1) = 12». За допомогою цього виразу ми можемо знайти константу «C». Замість «t» варто підставити «1», а замість «S(t)» ми маємо підставити «12». Матимемо:

12 = 1⁴ + 2 ∙ 1² + 2 ∙ 1 + C

12 = 1 + 2 + 2 + C

C = 7

Отже, конкретний вигляд функції «S(t)» буде:

S(t) = t⁴ + 2t² + 2t + 7

Маючи конкретний вигляд первісної функції «S(t)» ми можемо знайти значення «S(3)». Для цього замість «t» нам необхідно підставити «3». Матимемо:

S(3) = 3⁴ + 2 ∙ 3² + 2 ∙ 3 + 7 = 81 + 18 + 6 + 7 = 112

Відповідь: 112.

Завдання на фізичний зміст первісної можуть бути різноманітними. Наприклад, завдання може звучати так: «в який момент часу тіло (автомобіль для прикладу) зупиниться?». Зауважимо, що тіло зупиниться, якщо його швидкість рівна нулеві. Тобто, виконується умова «v(t) = 0». І, в такому випадку, вам необхідно знайти час («t»).

Схожа ситуація буде в завданнях такого типу: «через скільки часу тіло проїде якусь певну відстань» або «через скільки часу тіло матиме якусь конкретну швидкість/прискорення».

Як розумієте, типів завдань можна придумати доволі багато, тому вам необхідно практикувати.

Геометричний зміст первісної

За допомогою первісної можна обчислювати площу криволінійної трапеції. Для цього використовують визначений інтеграл:

S = a/b f(x) dx

На координатній площині криволінійна трапеція буде мати такий вигляд:

Зверніть увагу. На малюнку криволінійна трапеція знаходиться над віссю «Ox». Тому, інтеграл матиме знак «+», якщо трапеція знаходиться під віссю «Ox», то інтеграл буде мати знак «-». Тому, якщо у вас вийшло від’ємне число, то не варто панікувати. Перевірте де знаходиться графік функції. Детальніше ми це розглянемо пізніше.

Відповідно, маючи криволінійну трапецію в різних частинах від осі «Ox» вам варто при обчислені площі розділити інтеграл на різні частини.

На графіку це виглядатиме так:

Тоді, площу всієї фігури ми знайдемо так:

S = -a/c f(x) dx + c/b f(x) dx

Приклад: знайти площу фігури, обмеженої лініями «y = 8x - 6x²», «x = /1/2», «x = 1», «y = 0».

Межами інтегрування в нас є «/1/2 = 0,5» - нижня межа, «1» - верхня межа. Функція по якій обчислюємо первісну буде «8x - 6x²».

Отже, площу даної фігури ми можемо обчислити так:

0,5/1(8x - 6x²) dx = (8 ∙ x²2 - 6 ∙ x³3) 0,5/1 = (4x² - 2x³) 0,5/1 = (4 ∙ 1² - 2 ∙ 1³) - (4 ∙ (0,5)² - 2 ∙ (0,5)³) = 2 - 0,75 = 1,25

Відповідь: S = 1,25.

Зауважте, що в завданні ми мали дві функції «y». При цьому одна з них була прямою «y = 0» яка збігається з віссю «Ox». Ви можете мати фігуру обмежену двома кривими.

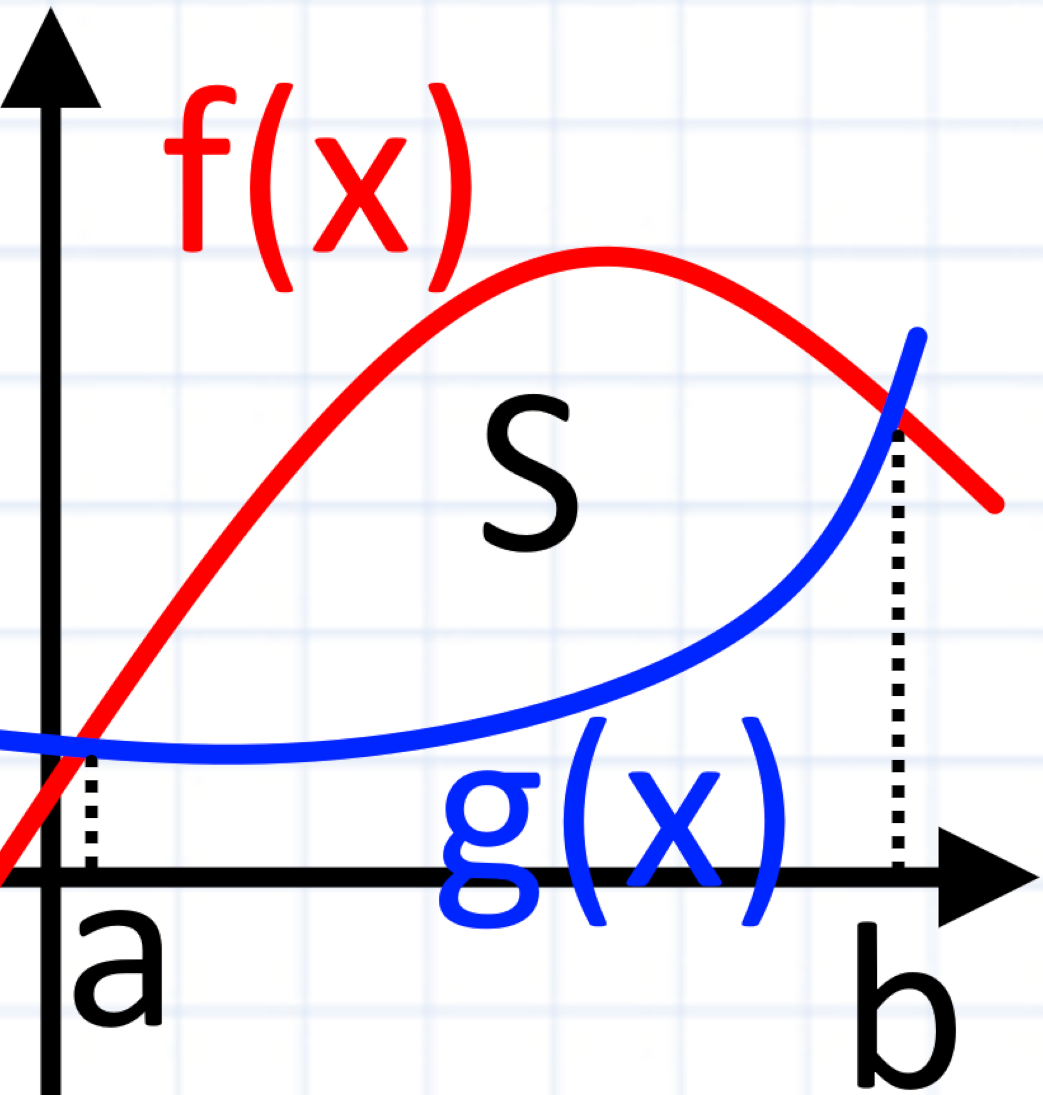
Щоб обчислити площу даної фігури нам необхідно скористатися формулою:

S = a/b [f(x) - g(x)] dx

Де «a», «b» - точки перетину графіків функцій; «f(x)» - верхня функція; «g(x)» - нижня функція.

Щоб визначити верхню та нижню є два варіанти:

Межі на яких відбувається інтегрування можуть бути задані відразу або ви можете їх знайти розв’язавши рівняння:

f(x) = g(x)

Зауважимо одну важливу деталь. Ви можете не визначати яка функція є з верху, а яка з низу. Ви можете віднімати в будь-якому порядку, але є важлива деталь. Якщо ви віднімете від нижньої функції верхню, то отримаєте від’ємну площу.

Само собою ви можете просто не враховувати знак «-». Але будьте обережні. Якщо ви зробили десь помилку, то результат також може вийти від’ємним. Тому, при від’ємному результатові ви не можете бути впевнені, що зробили все правильно.

Саме дана формула є поясненням, чому інтеграл функції яка знаходиться під віссю «Ox» буде від’ємним. Бо верхня функція це і буде вісь «Ox», тобто пряма «y = 0». А, нижньою функцією виступатиме задана.

Приклад: обчислити площу фігури, обмежену лініями «y = 6 - 2x», «y = 6 + x + x²».

В даному завданні межі інтегрування не вказані. Тому, нам необхідно їх знайти самостійно. Для цього, потрібно прирівняти наші функції та знайти розв’язки. Матимемо:

6 - 2x = 6 + x + x²

x² + 3x = 0

x₁ = 0; x₂ = -3

Отже, ми маємо межі інтегрування «-3» та «0».

Тепер, нам необхідно дізнатися яка з функцій буде з верху. Для цього потрібно підставити якесь число з проміжку «(-3; 0)». Наприклад: «-1». Матимемо:

y = 6 - 2x => y = 6 - 2 ∙ (-1) = 8

y = 6 + x + x² => y = 6 - 1 + (-1)² = 6

Як бачите, результат функції «y = 6 - 2x» є більшим. Тому, вона є верхньою. Отже, ми можемо обчислити площу фігури за так:

S = -3/0 [(6 - 2x) - (6 + x + x²)] dx = -3/0 [-3x - x²] dx = [-3 ∙ x²2 - x³3] -3/0 = (-3 ∙ 0²2 - 0³3) - (-3 ∙ (-3)²2 - (-3)³3) = -(-13,5 + 9) = 4,5

Відповідь: S = 4,5.

Об’єм

Ви можете знайти об’єм тіла яке утвориться в наслідок обертання криволінійної трапеції навколо осі «Ox». Це тіло виглядатиме так:

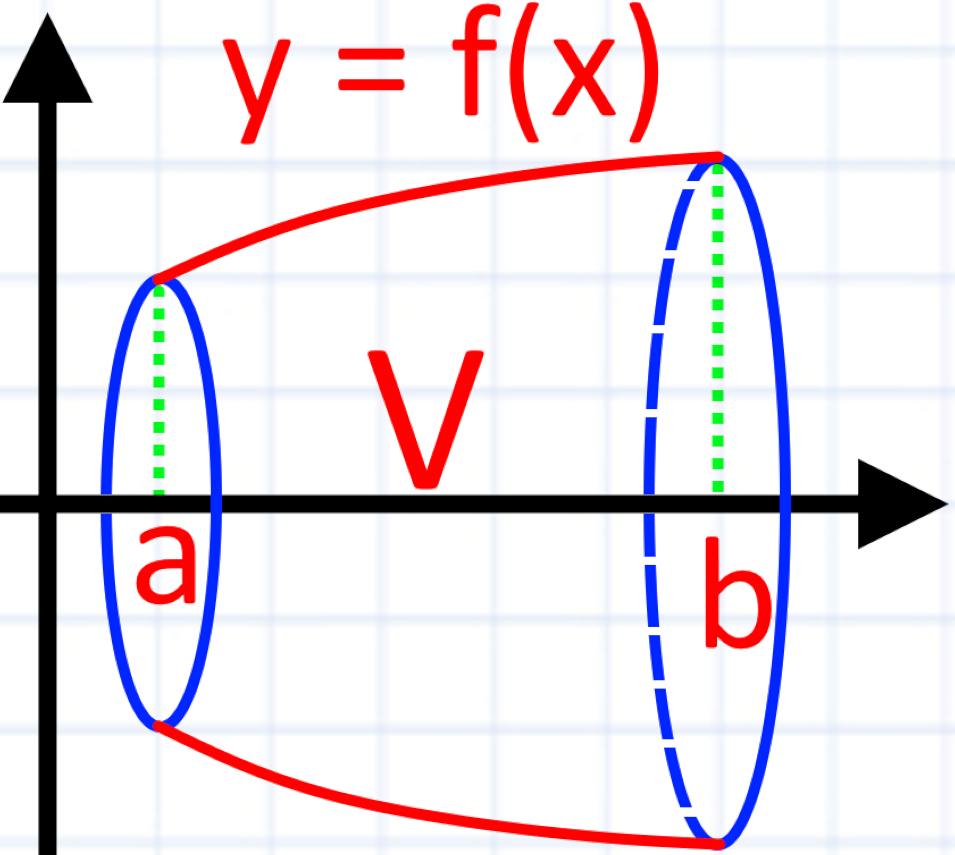
Формула для обчислення об’єму:

V = π a/b [f(x)]² dx

Приклад: обчислити об’єм тіла обмеженого лінією «y = sin ⁡x», де «x ∈ [0; /π/3 ]».

Напишемо це у вигляді інтеграла: «V = π ∫ ₀^π/3[sin ⁡x]² dx».

Піднімемо до квадрата й отримаємо: «π ∫ ₀^π/3 sin⁡ x dx».

Обчислимо первісну:

π ∫ ₀^π/3 sin ⁡x dx = π ∙ (- cos ⁡x) | ₀^π/3 = -π ∙(cos /π/3 ⁡-cos⁡ 0 ) = -π ∙ (/1/2 - 1) = -π ∙ (-/1/2) = /π/2 = 0,5π

Відповідь: 0,5π.