Означення чотирикутника

Чотирикутник — це фігура, що складається з чотирьох точок (вершин) та сторін (відрізків), що послідовно з'єднують ці вершини. При цьому жодні з цих трьох точок не лежать на одній прямій.

Вершини, називають сусідніми, якщо вони є кінцями однієї сторони. В іншому випадку їх називають протилежними.

Сторони які виходять з однієї вершини називають сусідніми. Сторони, які не мають спільної вершини, називаються протилежними.

Відрізок, що з’єднують протилежні вершини називається діагоналлю.

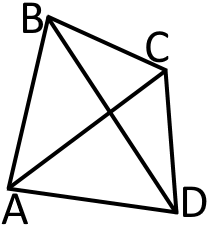
«ABCD» – чотирикутник. «A», «B», «C», «D» - вершини; «AB», «BC», «CD», «AD» - сторони; «AC», «BD» - діагоналі чотирикутника.

Сума всіх сторін чотирикутника називається периметром. Його позначають так «Р».

P = AB + BC + CD + AD

В будь якому чотирикутнику сума внутрішніх кутів рівна «360» градусів.

∠A + ∠B + ∠C + ∠D = 360

Правильним чотирикутником, називають чотирикутник сторони якого не перетинаються.

Не правильний (складний) чотирикутник — це чотирикутник сторони якого перетинаються між собою.

Чотирикутники є випуклими (увігнуті) та опуклими.

Чотирикутник в якого всі кути є меншими за «180» градусів та діагоналі знаходяться в середині, то такий чотирикутник називають опуклим.

Чотирикутник в якого один із кутів є більшим за «180» градусів, а одна із діагоналей знаходиться за межами чотирикутника, називається випуклим (увігнутим).

Квадрат, його властивості. Ознаки квадрата.

Квадрат – це чотирикутник у якого всі сторони рівні та всі кути є прямими.

Діагоналі квадрата рівні, перетинаються під прямим кутом та у точці перетину діляться пополам. Діагоналі квадрата також є його бісектрисами, тобто ділять його кути навпіл.

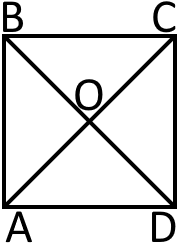
«AB», «BC», «CD», «AD» - сторони квадрата.

«AC», «BD» - діагоналі квадрата.

Прямокутник, його властивості. Ознаки прямокутника.

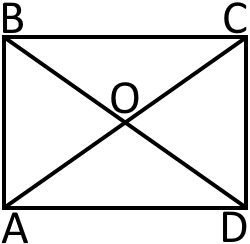
Прямокутник – це чотирикутник у якого всі кути прямі, а протилежні сторони є попарно паралельними та рівними.

Діагоналі прямокутника є рівними і в точці перетину діляться пополам.

class="NavigationInfo"Паралелограм, його властивості. Ознаки паралелограма.

Паралелограм – це чотирикутник, у якого протилежні сторони є попарно паралельними та рівними.

У паралелограмі протилежні кути рівні між собою. А сума двох сусідніх кутів рівна «180» градусів.

Діагоналі в точці перетину діляться пополам.

У паралелограма: сума квадратів діагоналей паралелограма дорівнює сумі квадратів усіх його сторін.

AC² + BD² = 2(AB² + BC²)

Ромб, його властивості. Ознаки ромба.

Ромб – це чотирикутник, у якого всі сторони рівні між собою.

У ромба протилежні кути рівні між собою.

Діагоналі в ромбі перетинаються під прямим кутом та в точці перетину діляться пополам. Діагональ ділить кут ромба пополам.

Трапеція, її властивості та види. Середня лінія трапеції.

Трапеція – це чотирикутник, у якого дві сторони паралельні, а дві інші не паралельні. Паралельні сторони називаються основами. Не паралельні сторони називаються бічними сторонами.

Сума кутів трапеції, прилеглих до бічної сторони, дорівнює «180» градусів.

Трапеції є трьох видів: різностороння, прямокутна, рівнобічна.

Різностороння трапеція

Трапецію називають різносторонньою, якщо її бічні сторони є різної довжини та кути при одній основі є різними.

Рівнобічна трапеція

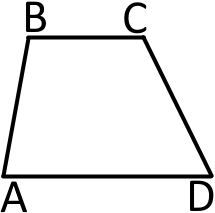
Трапецію називають рівнобічною, якщо її бічні сторони є рівними.

У рівнобічній трапеції кути при основі рівні.

Діагоналі у рівнобічній трапеції рівні.

Прямокутна трапеція

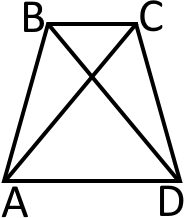
Трапецію називають прямокутною, якщо один з її кутів (при кожній з основ) прямий.

Середня лінія трапеції

Середня лінія трапеції – це лінія, що з’єднує середини бічних сторін та є паралельною її основам. При цьому довжина середньої лінії рівна половині суми основ трапеції.

«МН» - середня лінія трапеції. «AB» та «CD» - основи трапеції. Тоді, матимемо:

MH = /AB + CD/2

AH = BH = /AB/2

CM = DM = /CD/2

Властивість трапеції:

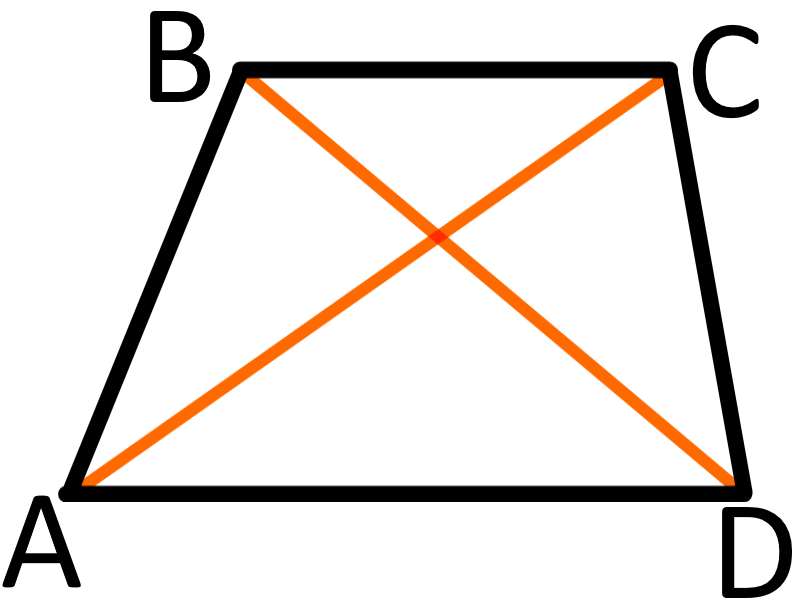
Сума квадратів діагоналей дорівнює сумі квадратів бічних сторін плюс подвоєний добуток основ:

AC² + BD² = AB² + CD² + 2AD∙BC

Вписані та описані чотирикутники

Чотирикутник є вписаним у коло тоді, коли всі його вершини належать цьому колу.

Коли чотирикутник вписаний у коло, то сума його внутрішніх кутів дорівнює «180» градусів.

∠A + ∠C = 180^о

∠B + ∠D = 180^о

Чотирикутник є описаним навколо кола тоді, коли коло дотикається до всіх його сторін (сторони чотирикутника є дотичними до кола).

Коли чотирикутник описаний навколо кола, то суми його протилежних сторін є рівними.

AB + CD = AD + BC