Нерівності виду «a^f(x) > b», «a^f(x) ≥ b», «a^f(x) < b», «a^f(x) ≤ b», де «a > 0», «a ≠ 1».

Для будь-яких значень «а» при «a > 0», «a ≠ 1» вираз «a^f(x)» завжди буде більшим за нуль. Тобто: «a^f(x) > 0». То у такому випадку, коли «b» буде меншим або рівним нулеві («b ≤ 0») розв’язками нерівностей «a^f(x) > b», «a^f(x) ≥ b» буде вся множина «R» (тобто: «(-∞; +∞)»), а нерівності «a^f(x) < b», «a^f(x) ≤ b» не мають розв’язків.

Коли ми маємо, що «b» є більшим за нуль («b > 0»), то такі нерівності розв’язуються так же як і рівняння вигляду «a^f(x) = b» єдина різниця, що тут використовується знак нерівності. Тобто рівняння «a^f(x) = b» розв’яжемо так «f(x) = log_ab». Детальніше читайте тут. У нерівностях нам необхідно звернути увагу на основу («а»). Якщо, основа буде в межах від нуля до одиниці («0 < a < 1»), то у момент, коли ми знаходитимемо «f(x)» необхідно змінити знак нерівності на протилежний, а коли основа «a» буде більшою за одиницю («a > 1»), то знак нерівності змінювати не потрібно.

Розв’язок будь-якої нерівності (у таблиці буде продемонстровано варіант нерівності «a^f(x) ≥ b») можна подати у вигляді таблиці:

Також, якщо число «b» можна переписати у вигляді «a^c» («b = a^c»), де «c» - деяке число, то відповідно будемо мати (продемонстровано на нерівності вигляду «a^f(x) ≥ a^c»):

Після чого залишається розв’язати отриману нерівність. Детальніше про прості, квадратні, складні нерівності читайте на сайті.

Приклад: 5^x > 5

5^x > 5¹

x > 1

x ∈ (1; +∞)

Приклад 2: 2^x < /1/8

Оскільки «/1/8» ми можемо переписати як «2» у степені «-3» («/1/8 = 2^-3»), то наша нерівність буде мати такий вигляд:

2^x < 2^-3

x < -3

x ∈ (-∞; -3)

Приклад 3: 4^x > 3

x > log₄⁡3

x ∈ (log₄⁡3; +∞)

Приклад 4: 0,7^x < 1

Ми можемо «1» переписати як «0,7⁰», тоді наший вираз набуде такого вигляду:

0,7^x < 0,7⁰

Оскільки, основа («0,7») є в межах від нуля до одиниці («0 < 0,7 < 1»), то знак нерівності зміниться на протилежний:

x > 0

x ∈ (0; +∞)

Нерівності вигляду «a^f(x) > a^g(x)», «a^f(x) ≥ a^g(x)», «a^f(x) < a^g(x)», «a^f(x) ≤ a^g(x)», де «a > 0», «a ≠ 1».

Будемо демонструвати на нерівності вигляду: «a^f(x) ≥ a^g(x)».

У попередньому типі нерівності «a^f(x) ≥ b» було вказано, якщо ми можемо «b» переписати у вигляді «a^c», де «с» - будь-яке чисто, то отримаємо нерівність вигляду «a^f(x) ≥ a^c». Яку можна розв’язати так:

Нерівність «a^f(x) ≥ a^g(x)» можна розв’язати за тим же принципом. Покажемо у вигляді таблиці:

Приклад: 7^x - 7^1_x > 0

Оскільки, у цьому прикладі у нас є лише два числа і обидва числа містять «х» у степені, то ми можемо перенести «-7^1_x» у протилежну сторону. Після чого отримаємо:

7^x > 7^1_x

В нашому прикладі основи є вже однаковими, тому залишається порівняти їх степені. Основи є більшими за одиницю, тому нам не потрібно змінювати знак нерівності на протилежний. Отже, будемо мати:

x > /1/x

Перенесемо все в одну сторону для того щоб порівнювати з нулем.

x - /1/x > 0

Та зведемо все до одного єдиного виразу. Тобто, зробимо один єдиний дріб.

x² - 1x > 0

Ми отримали складну нерівність. Детальніше як їх розв’язувати читайте тут.

Розіб’ємо нашу нерівність на систему нерівностей:

{ x² - 1 > 0 x > 0

Друга нерівність є вже розв’язаною, тому залишається розв’язати лише першу нерівність.

x² - 1 > 0

Оскільки, це є квадратна нерівність, то її зручно розв’язувати прирівнявши до нуля.

x² - 1 = 0

x² = 1

x = ± √1

x = ±1

Нанесемо всі розв’язки на одну єдину пряму.

Знак нерівності «x² - 1 > 0» будемо позначати синім кольором, а знак нерівності «x > 0» - червоним. Загальний знак нерівності «x² - 1x > 0» позначимо зеленим кольором:

Нам підходять проміжки зі загальним знаком «+», тому розв’язками початкової нерівності буде:

x ∈ (-1; 0) ∪ (1; +∞)

Приклад 2: 9^{x + 5} ≥ 27^x

В нашому прикладі основи є різними, але враховуючи, що ми можемо «9» та «27» подати як «3» в якомусь степені, то нашу нерівність можна переписати через основу «3». Врахуємо, що «9 = 3²», «27 = 3³» і будемо мати:

3^{2(x + 5)} ≥ 3^3x

Оскільки, основи є рівними, то нам залишається порівняти їх степені. Враховуючи, що основа більша за одиницю, то знак нерівності змінювати не потрібно. Будемо мати:

2(x + 5) ≥ 3x

Отримали лінійну нерівність. Детальніше можете прочитати тут. Розв’яжемо її.

2x + 10 ≥ 3x

2x - 3x ≥ -10

-x ≥ -10 | ∙ (-1)

x ≤ 10

Отже, розв’язком початкової нерівності буде проміжок:

x ∈ (-∞; 10]

Складні показникові нерівності.

При розв’язувані складних показникових нерівностей використовують ті ж самі методи, що й при розв’язуванні складних показникових рівнянь: винесення спільного множника за дужки, заміну змінних, ділення на один з виразів тощо. Головна мета цих дій це звести складну показникову нерівність до одного з виглядів найпростішої показникової нерівності.

Приклад: 3^x > 5^x

Оскільки, в нашій нерівності є різні основи але степені однакові, то щоб розв’язати дану нерівність варто поділити на один з виразів «3^x» або «5^x». Враховуючи, що обидва вирази при будь-яких значеннях «х» будуть більшими за нуль, то знак нерівності змінювати не потрібно. Поділимо на «5^x», отримаємо:

3^x > 5^x | ∶ 5^x

3^x5^x > 5^x5^x

3^x5^x > 1

Винесемо степінь «х» за дужки:

(/3/5)^x > 1

Для своєї зручності «1» ми можемо написати як «(/3/5)⁰»:

(/3/5)^x > (/3/5)⁰

Отже, ми отримали найпростішу нерівність вигляду «a^f(x) > a^c». Враховуючи, що основи у нас рівні, то необхідно порівняти їх степені. Але основа є в межах від нуля до одиниці, тому знак нерівності необхідно змінити на протилежний.

x < 0

Отже, розв’язок початкової нерівності буде проміжок:

x ∈ (-∞; 0)

Приклад 2: 2^{x + 1} + 2^x < 24

Вирази які мають змінну «х» у степені є з однаковими основами але мають різні степені.

Скористаємося властивістю степеня «a^{x + y} = a^x ∙ a^y» та перепишемо «2^{x + 1}» так «2^x ∙ 2». Після чого наша нерівність виглядатиме так:

2^x∙2 + 2^x < 24

Як помітно в лівій частині є спільний множник «2^x». Винесемо його за дужки. Отримаємо:

2^x(2 + 1) < 24

2^x ∙ 3 < 24

Поділимо весь вираз на «3»:

2^x ∙ 3 < 24 | ∶ 3

2^x < 8

Отримали найпростішу нерівність вигляду «a^f(x) < b». ЇЇ можна розв’язати так:

f(x) < log_a⁡b

Будемо мати:

x < log₂⁡8

x < 3

Отже, розв’язок початкової нерівності буде такий:

x ∈ (-∞; 3)

Приклад 3: 9^x - 3^{x + 1} + 2 > 0

Як помітно у цьому прикладі ми маємо різні степені та різні основи. Спробуємо зробити однакові вирази які будуть містити степінь з «х». Для цього «9» напишемо як «3²»: «9^x = (3²)^x = (3^x)²», а «3^{x + 1}» розкладемо за властивістю степеня «a^{x + y} = a^x ∙ a^y» та отримаємо «3^x ∙ 3». Після чого наша нерівність буде мати такий вигляд:

(3^x)² - 3∙3^x + 2 > 0

Тепер зручно скористатися заміною змінної «3^x = t» після чого ми отримаємо:

t² - 3t + 2 > 0

Розв’яжемо цю нерівність як квадратну. Для цього прирівняємо до нуля та знайдемо розв’язки квадратного рівняння:

t² - 3t + 2 = 0

D = (-3)² - 4∙1∙2 = 9 - 8 = 1

t₁ = /-(-3) + √1/2 ∙ 1 = 2

t₂ = /-(-3) - √1/2 ∙ 1 = 1

Нанесемо на координатну пряму наші точки на побудуємо ескіз параболи.

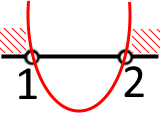
Розв’язок нерівності «t² - 3t + 2 > 0» напишемо у вигляді системи:

{/t < 1/t > 2

Повернемося до старої змінної та розв’яжемо нерівності відносно неї:

При «t < 1»:

3^x < 1

3^x < 3⁰

x < 0

При «t > 2»:

3^x > 2

x > log₃⁡2

Остаточним розв’язком початкової нерівності буде:

x ∈ (-∞; 0)∪(log₃⁡2; +∞)

Приклад 4: 8^x + 18^x - 2∙27^x > 0

В даній нерівності у нас є однаковий степінь але різні основи. Спробуємо все звести до однієї основи. Для цього перепишемо «8^x», «18^x», «27^x» так:

8^x = (2³)^x = 2^3x

18^x = (2∙9)^x = 2^x∙9^x = 2^x∙(3²)^x = 2^x∙3²x

27^x = (3³)^x = 3^3x

Тепер наша нерівність виглядає так:

2^3x + 2^x∙3^2x - 2∙3^3x > 0

Поділимо всю нерівність на «3^3x». Враховуючи, що «3^3x» буде завжди більшою за нуль при будь-яких значеннях «х», то знак нерівності не потрібно змінювати на протилежний. Матимемо:

2^3x + 2^x∙3^2x - 2∙3^3x > 0 |∶3^3x

2^3x3^3x + 2^x∙3^2x3^3x - 2∙3^3x3^3x >0

Тепер варто спростити нашу нерівність. З виразу «2^3x3^3x» ми можемо винести степінь «3х» за дужки і отримаємо «(/2/3)^3x = ((/2/3)^x)³». У виразі «2^x∙3^2x3^3x» у нас скоротиться «3^2x» та «3^3x» і отримаємо «2^3x3^3x», після чого винесемо степінь «х» за дужки і отримаємо «(/2/3)^x». Вираз «3^3x3^3x» повністю скоротиться та отримаємо «1». В кінцевому результаті будемо мати такий вигляд:

((/2/3)^x)³ + (/2/3)^x - 2 > 0

Скористаємося заміною змінної:

(/2/3)^x = t

Будемо мати:

t³ + t - 2 > 0

Для зручності прирівняємо до нуля.

t³ + t - 2 = 0

Розкладемо «-2» на «– 1 – 1»:

t³ + t - 1 - 1 = 0

Згрупуємо наший приклад на дві пари: «t³ - 1» та «t - 1».

t³ - 1 + t - 1 = 0

Пару «t³ - 1» розкладемо за формулою скороченого множення «a³ - b³ = (a - b)(a² + ab + b²)» та отримаємо:

(t - 1)(t² + t + 1) + (t - 1) = 0

Ми отримали спільний множник «(t - 1)» який винесемо за дужки:

(t - 1)[(t² + t + 1) + 1] = 0

У других дужках («[…]») розкриємо внутрішні дужки та виконаємо дії з подібними числами.

(t - 1)[t² + t + 1 + 1] = 0

(t - 1)[t² + t + 2] = 0

Оскільки при множені двох чисел (дужок) вийшов нуль, то це означає, що одна з цих дужок може бути нуль:

t - 1 = 0; або t² + t + 2 = 0

Розв’яжемо перші дужки:

t - 1 = 0

t = 1

Розв’яжемо другі дужки:

t² + t + 2 = 0

D = 1² - 4∙1∙2 = 1 - 8 = -7

t ∈ ∅

Отже, розв’язком нерівності «t³ + t - 2 > 0» буде:

t > 1

Повернемося до нашої заміни:

(/2/3)^x > 1

(/2/3)^x > (/2/3)⁰

Оскільки, основа є в межах від нуля до одиниці («0 < /2/3 < 1»), то знак нерівності варто змінити на протилежний:

x < 0

Остаточний розв’язок початкової нерівності буде проміжок:

x ∈ (-∞; 0)

Приклад 5: 25∙2^x - 10^x + 5^x > 25

Перенесемо «25» з правої частини у ліву:

25∙2^x - 25 - 10^x + 5^x > 0

Розкладемо «10^x» за правилом «(a ∙ b)ⁿ = aⁿ ∙ bⁿ» отримаємо «10^x = (2∙5)^x = 2^x∙5^x» і наша нерівність набуде такого вигляду:

25∙2^x - 25 - 2^x∙5^x + 5^x > 0

Згрупуємо наші числа. З «25∙2^x - 25» винесемо за дужки «25», а з «-2^x∙5^x + 5^x» винесемо «-5^x». Наша нерівність набуде такого вигляду:

25(2^x - 1) - 5^x(2^x - 1) > 0

У нас з’явився спільний множник «(2^x - 1)». Винесемо його за дужки та отримаємо:

(2^x - 1)(25 - 5^x) > 0

Розіб’ємо на систему нерівностей:

{ 2^x - 1 > 0 25 - 5^x > 0

{ 2^x>1 -5^x > -25 |∙(-1)

{ 2^x > 1 5^x < 25

{ 2^x > 2⁰ 5^x < 5²

{ x > 0 x < 2

Нанесемо наші розв’язки на координатну пряму, де розв’язок нерівності «x > 0» позначимо червоним, а «x < 2» - синім та знайдемо спільний знак нерівності. А спільну частину виділимо зеленим.

Кінцевий розв’язок початкової нерівності буде такий:

x ∈ (0; 2)

Приклад 6: 2^x2 > sin ⁡x

Оскільки, «sin ⁡x» є обмеженою функцією в межах від «-1» до «1» («-1 ≤ sin ⁡x ≤ 1»), а вираз «2^x2» є більшим за один («2^x2 ≥ 1») для будь-яких значень змінної «х» (значення менші за одиницю не можуть бути, оскільки, вираз «2^x2» не набуває від’ємних значень завдяки квадрату) і лише при «х = 0» наший вираз буде рівний «1» але при «х = 0» будемо мати «sin 0 = 0». Тому розв’язком початкової нерівності буде вся множина дійсних чисел:

x ∈ R