Розв'язування рівнянь, що зводяться до лінійних або квадратних рівнянь
Дробові раціональні рівняння
Часто зустрічаються дробово раціональні рівняння. Це рівняння у яких є змінна в знаменнику. Зазвичай з ними виникає найбільше труднощів. Розглянемо декілька способів як їх розв’язувати. Вони є між собою доволі подібні. Розберемо їх відразу на прикладах.
Дробово раціональні рівняння зручно розв’язувати в такому вигляді:
/A/B = 0
Де «А» - чисельник, а «В» - знаменник дробу.
Після чого необхідно розв’язати таку систему:
{/A = 0/В ≠ 0
Після розв’язання цієї системи необхідно викинути з «розв’язків» усі «не розв’язки».
Наприклад:
{/х = 5; х = -2/х ≠ 2; х ≠ -2
Як бачите є «не розв’язки» «х ≠ 2; х ≠ -2» і їх необхідно викинути. Оскільки з «розв’язками» збігається лише « х≠ -2», то «розв’язок» «х = 2» відкидаємо. Після, чого залишається лише «х = 5».
Отже: «/a/b = 0» , тоді й тільки тоді, коли "a = 0" i "b ≠ 0".
Наприклад:
/x - 3/x + 5 = 0
В такому випадку дріб рівний нулю лише коли його чисельник рівний нулю, а знаменник не рівний нулю.
{/x - 3 = 0/х + 5 ≠ 0
{/x = 3/х ≠ -5
Відповідь: 3.
Бувають випадки, коли є дріб та ще один або декілька дробів чи виразів. Тоді краще за все перенести їх в одну частину (якщо вони знаходяться в різних частинах рівняння) та звести їх до одного дробу (звести до спільного знаменника).
Наприклад:
/3/x - 1 = 0
Зведемо до спільного знаменника.
/3 - x/x = 0
В такому випадку дріб рівний нулю лише коли його чисельник рівний нулю, а знаменник не рівний нулю. Та отримаємо таку систему:
{/3 - x = 0/х ≠ 0
{/x = 3/х ≠ 0
Відповідь: х = 3.
Якщо у вас є лише два дроби або дріб та число, то щоб не зводити до одного дробу можна використати такі властивості:
Умови рівності двох дробів з однаковими знаменниками:
/a/b = /c/b
Tоді й тільки тоді, коли "a = c" i "b ≠ 0".
/2x + 1/x + 1 = /x - 3/x + 1
Щоб знайти розв’язок необхідно відкинути варіанти коли знаменник рівний нулю, тобто x+1≠0; x≠-1. Після чого необхідно прирівняти чисельники:
2x + 1 = x - 3
Після цього необхідно розв’язати отримане рівняння.
2x - x = -3 - 1
x = -4
Рівність двох дробів:
Цей спосіб подібний до попереднього і відрізняється лише тим, що знаменники у дробів різні.
/a/b = /c/d;
Такі приклади розглядають як пропорцію, тоді – основна властивість пропорції. Це доволі легко запам’ятати, якщо уявити метелика.
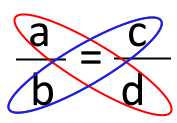
Розглянемо приклад:
/3 + x/x + 1 = /x - 1/x
Важливо відразу знайти значення при яких знаменник стає нульовим (рівним нулю). І відкинути ці значення.
і
Далі необхідно скористатися основною властивістю пропорції (спосіб метелика).
(3 + x)x =
3x + x2 = x2 - 1
3x + x2 - x2 = -1
3x = -1
x = -/1/3
Цим способом також зручно користуватися, коли в одній частині є дріб, а в іншій число.
/2x - 3/x + 1 = 5
Відразу вказуємо, що Та для своєї зручності пишемо під «5» уявну одиницю в знаменнику.
/2x - 3/x + 1 = /5/1
Після чого користуємося «метеликом» та отримаємо:
2x - 3 = 5(x + 1)
Після чого залишається лише розв'язати отримане рівняння.
Розв’яжемо приклад з декількома дробами.
Коли є дробове раціональне рівняння з декількома доданками (дробами), то можна звести цей приклад до вигляду
Приклад:
/1/x + 2 - 12x - x2 = 8x3 - 4x
Перенесемо все в одну частину (зробимо в одній частині).
/1/x + 2 - 12x - x2 - 8x3 - 4x = 0
Розкладемо на множники знаменники дробів.
/1/x + 2 - /1/x(2 - x) - /8/x(x-2)(x+2) = 0
На даний момент спільний знаменник виглядає так: . Але зверніть увагу на другий дріб. Перед ним стоїть знак мінус також в знаменнику в дужках є такий вираз Можна в нести знак мінус у дужки, тоді сам знак стане додатнім, а в дужках доданки змінять свої знаки на протилежні (тобто, ми помножимо на
Ось як рівняння виглядатиме після цих дій:
/1/x + 2 + /1/x(x - 2) - /8/x(x-2)(x+2) = 0
І тепер спільний знаменник виглядає так:
Отже зведемо наші дроби до спільного знаменника (як правильно це зробити читайте «дії з дробами»):
Отримаємо:
/x(x - 2) + (x + 2) - 8/x(x - 2)(x + 2) = 0
Отримавши спільний знаменник - пам’ятаємо, що він не дорівнює нулю. Тобто:
i
Тепер необхідно розв’язати рівняння, що знаходиться у чисельнику.
Отже отримаємо:
Розкриємо дужки та виконаємо дії. Результат:
x2 - x - 6 = 0
Залишається розв’язати квадратне рівняння.
- дискримінант більший нуля. Отже буде два корені
Після того як були знайденні всі корені рівняння потрібно перевірити чи при них знаменник не буде рівний нулю. Оскільки ми раніше знайшли, що спільний знаменник буде рівний нулю при то розв’язок не задовольняє рівняння.
Відповідь: 3 – корінь початкового рівняння.
Отже можна виділити загальні кроки для розв’язування дробових раціональних рівнянь:
1. Знайти спільний знаменник дробів, що входять у рівняння
2. Домножити обидві частини рівняння на спільний знаменник
3. Розв’язати отримане ціле рівняння, врахувавши допустимі значення змінної (знайти при якому значенні «х» спільний знаменник перетворюється у нуль)
4. Виключити з коренів ті, які перетворюють в нуль спільний знаменник
5. Записати відповідь
6. Виконати перевірку
Метод розкладання многочлена на множники:
У випадках, коли в правій частині рівняння стоїть нуль а у лівій многочлен, то таке рівняння можна розв’язати за допомогою розкладання многочлена на множники.
Розв’яжемо рівняння:
x3 + 3x2 - 4x = 0
У всіх доданках в лівій частині є як мінімум один «х», отже можна винести його як спільний множник. Після цього наше рівняння набуде такого вигляду:
x(x2 + 3x - 4) = 0
У лівій частині виникли два множника, перший «х», другий У цьому і полягає метод розкладання на множники. Щоб у рівнянні не залишилося доданків. Тобто щоб дії додавання та віднімання були лише в дужках але не за їх межами.
Оскільки в лівій частині знаходяться множники, а в правій нуль, то це означає, що один з множників рівний нулю.
Тобто: "x = 0" або "x2 + 3x - 4 = 0"
1) х = 0
2) x2 + 3x - 4 = 0
- дискримінант більший нуля, отже буде два дійсних корені
x1 = /-3 + √25/2 = 1
x2 = /-3 - √25/2 = -4
Варто зауважити, що скільки множників стільки ж і рівнянь буде рівних нулеві.
Наприклад: - в такому випадку буде три рівняння.
або або
Після чого залишиться лише розв’язати рівняння які утворилися.
Розглянемо ще один приклад:
x3 - 3x2 + x - 3 = 0;
Винесемо з перших двох доданків та візьмемо у дужки (третій та четвертий доданок) для наглядності:
x2(x - 3) + (x - 3) = 0
Як видно в обох доданках є Винесемо його за дужки.
(x2 + 1)(x - 3) = 0
Оскільки зліва стоїть нуль, а справа залишилися лише множники отже все добре. Тепер можна розділити рівняння:
або
1) x2 = -1; – розв’язків не має
2) x = 3
Часто буває, що доданки не вдається розділити на множники. В такому випадку необхідно шукати інші способи вирішити рівняння.
Біквадратні рівняння
Рівняння виду де називають біквадратним рівнянням. Таке рівняння розв’язується аналогічно як і звичайне рівняння, але з самого початку необхідно ввести нову змінну Після цього рівняння набуде стандартного вигляду.
Знайшовши його корені, необхідно повернутися до змінної У біквадратних рівняннях може бути від нуля (дійсних коренів не має) до чотирьох коренів рівняння (розв’язків) або безліч.
Розв’яжемо декілька прикладів:
x4 - 5x2 - 36 = 0
В першу чергу необхідно зробити замінну змінних «t = x2, t2 = x4», після цього початкове рівняння набуде такого вигляду:
t2 - 5t - 36 = 0
Розв’яжемо це рівняння:
рівняння має два корені
Після цього необхідно повернутися до замінної
Оскільки ми отримали два розв'язки при змінній то і необхідно двічі повернутися до нашої заміни підставивши кожен з результатів:
1. x2 = 9
2. не має розв’язків.
Отже початкове рівняння має корені:
Приклади для самостійного розв'язання:
2x4 + 3x2 + 4 = 0;
4x4 - 12x2 + 9 = 0;
2x4 + 10x2 - 72 = 0
Метод заміни змінних
Замінна змінних використовується не лише у біквадратних рівняннях, а й у деяких інших. Це буває необхідно для того щоб спростити рівняння. Розглянемо це на прикладі:
Щоб не розкривати дужки можна зробити заміну змінних «t=x2+3». Після цього отримаємо таке рівняння:
заміни змінних вийшло просте квадратне рівняння яке на багато простіше розв’язати.
Розв’яжемо його:
більший за нуль, отже, буде два корені рівняння.
t1 = /14 + √100/2 = /14 + 10/2 = 12
t2 = /14 - √100/2 = /14 - 10/2 = 2
Після того як були знайдені корені рівняння необхідно повернутися до заміни змінних.
1) x2 + 3 = 12
x2 = 12 - 3
x2 = 9
x1 = 3; x2 = -3
2) x2 + 3 = 3
x2 = 3 - 3
x2 = 0
x3 = x4 = 0 - корені однакові
Отже корені (розв’язки) початкового рівняння
Приклади для самостійного розв'язання:
(x2 - 2x - 1)(x2 - 2x - 3) = 3
Дільники вільного члену
Часто буває, що жодним зі способів не вдається вирішити рівняння. В такому випадку варто спробувати ще один спосіб. Ним не часто користуються через великі затрати по часу. Спосіб заключається у тому щоб знайти числа на які вільний член (число, що стоїть без «х») ділиться націло (не має остачі) при цьому не зважають на знак (наприклад, якщо вільний член то він ділиться як на так і на Після цього необхідно по черзі підставляти ці числа у рівняння та перевіряти чи вийде нуль Якщо вийшов нуль це означає, що дане число є коренем рівняння.
Цей спосіб використовують коли рівняння є третього та вище порядку (порядок рівняння визначається по найбільшому степені « рівняння п’ятого порядку). Варто зауважити, що максимальна кількість розв’язків не може бути більшою за порядок рівняння. Тобто, не може бути шість коренів у рівнянні п’ятого порядку.
Розв’яжемо рівняння:
x5 + x3 - x + 1 = 0
Вільним членом є а його дільниками Підставимо ці дільники у рівняння.
Підставляємо «1»:
не вийшов, отже «1» не є коренем рівняння.
Підставляємо «-1»:
нуль, отже «-1» є коренем рівняння.