Трикутником називають фігуру, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які сполучають ці точки. Точки називають вершинами трикутника, а відрізки – сторонами.

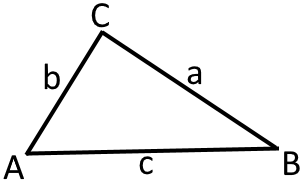
На малюнку зображено трикутник «АВС». Його вершинами є точки «А», «В», «С», а сторонами відрізки «АВ», «ВС» і «АС» або «a», «b», «c» (сторони позначають або двома великими літерами або однією маленькою). Щоб не писати кожного разу слово «трикутник», його заміняють символом «∆».

Кутами трикутника «АВС» називають кути «ВАС», «АВС» і «ВСА» або їх ще позначають однією буквою «∠A», «∠B» і «∠C».

У трикутнику навпроти найбільшої сторони знаходиться найбільший кут, найменшої – найменший і відповідно, навпроти рівних сторін знаходяться рівні кути.

Сума всіх внутрішніх кутів трикутника (тих кутів, що знаходяться в середині трикутника) рівна «180» градусів.

Зовнішнім кутом трикутника при даній вершині називається кут, суміжний з кутом трикутника при цій вершині.

Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним.

На малюнку кути «4», «5» та «6» є зовнішніми. Для того щоб зобразити зовнішній кут необхідно продовжити одну зі сторін трикутника і кут від цього продовження до іншої сторони буде зовнішнім. Зовнішній та внутрішній кут, що знаходяться біля однієї вершини є суміжними. «∠6 = ∠1 + ∠2», «∠1 + ∠4 = 180⁰».

Сума зовнішніх кутів взятих по одному при кожній вершині буде рівна «360» градусів.

∠4 + ∠5 + ∠6 = 360⁰

Важливо пам’ятати, що кожна сторона трикутника менша за суму двох інших сторін. Таку властивість називають нерівністю трикутника. «a < b + c»; «b < a + c»; «c < a + b» з відси можна зробити висновок, що «a > b - c» і «a > c – b». Узагальнюючи це, отримаємо: «a > |b – c|». Отже, кожна сторона трикутника менша за суму двох інших сторін, але більша від модуля їх різниці.

|b - c| < a < b + c

Дану нерівність можна скласти з будь-якою стороною трикутника.

Периметр трикутника – це довжин усіх його сторін. Периметр позначають буквою «Р». Також часто індексами вказують якої саме фігури це периметр (часто так роблять, якщо є декілька периметрів). Наприклад периметр трикутника «АВС» можна записати так «P_∆ABC». Отже «P_∆ABC = АВ + ВС + АС» або «P_∆ABC = a + b + c».

Медіана, бісектриса, висота

Медіана:

Медіаною трикутника називають відрізок, що сполучає вершину трикутника із серединою протилежної сторони.

Медіани будь-якого трикутника перетинаються в одній точці (вона називається центроїдом трикутника) і діляться цією точкою у відношенні «2:1», починаючи від вершини.

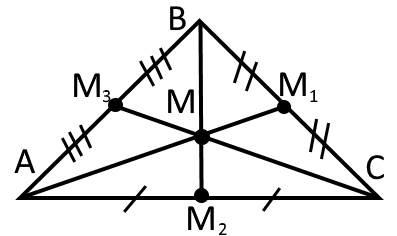
Точки «М₁», «М₂», «М₃» - основи медіан. Будь який трикутник має три медіани. «АМ₁», «ВМ₂», «СМ₃» - медіани трикутника «АВС».

Точка «М» - центроїд трикутника. Тоді «AM ∶ MM₁ = BM ∶ MM₂ = CM ∶ MM₃ = 2 ∶ 1» і «AM = /2/3 · AM₁; MM₁ = /1/3 · AM₁; BM = /2/3 · BM₂; MM₂ = /1/3 · BM₂; CM = /2/3 · CM₃; MM₃ = /1/3 · CM₃».

Довжину медіани трикутника «m_a», проведену до сторони «a», можна знайти за формулою:

або

Де «b» і «c» - сторони трикутника, між якими проходить медіана.

Якщо ви маєте всі три медіани трикутника, то можна знайти будь-яку сторону трикутника:

a = /2/3 · 2m/b/2 + 2m/c/2 - m/a/2

Бісектриса:

Бісектрисою трикутника називають відрізок бісектриси кута, що сполучає вершину трикутника з точкою протилежної сторони.

Якщо простими словами, то бісектриса ділить кут по полам (на два однакові кути які рівні половині початкового кута).

Будь який трикутник має три бісектриси. Відрізки «AL₁», «BL₂», «CL₃» - бісектриси трикутника «АВС». Точки «L₁», «L₂», «L₃» - основи бісектрис.

У будь-якому трикутнику бісектриси перетинаються в одній точці. Цю точку називають інцентром. На малюнку «І» - інцентр трикутника.

Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні двом іншим сторонам.

Наприклад: «ABBL₁ = ACL₁C» або можна записати ще так «/AB/AC = BL₁L₁C». Тобто пропорція складається за таким принципом: ліва сторона відноситься до лівого відрізку так само як і права сторона до правого. При складані пропорції важливо розуміти послідовність запису. Якщо в одній частині пропорції (наприклад з ліва від «=») стоїть першим сторона, а потім відрізок, то така ж послідовність має бути в іншій частині пропорції. Або, якщо в одній частині з почату стоїть права сторона, а потім ліва, то в іншій частині має бути правий відрізок, а потім лівий.

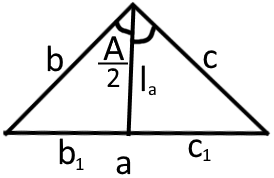
Довжину бісектриси трикутника «l_a», проведену до сторони «а» можна знайти за формулами:

Де «b», «c» - сторони трикутника; «b₁», «c₁» - відрізки сторони «a», на які її ділить бісектриса.

Або ще можна скористатися такою формулою:

Висота:

Висотою трикутника називають перпендикуляр, проведений із вершини трикутника до прямої, що містить його протилежну сторону. Висота це найкоротша відстань від вершини трикутника до сторони.

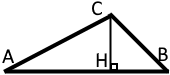
У будь якому трикутнику можна провести три висоти. Варто знати, що висоти можуть бути проведені не до самої сторони, а до її продовження (будуть знаходитися за межами трикутника).

Перетин висот, що проведені до сторін трикутника

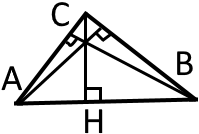
Перетин висот, що проведені до продовжень сторін трикутника

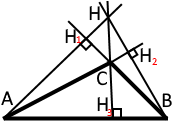
Варто зауважити, що висоти можуть перетинатися коли якась частина з них буде проведена до сторін трикутника, а інша до продовження сторін трикутника.

Відрізки «АН₁», «ВН₂», «СН₃» - висоти трикутника «АВС». Точки «Н₁», «Н₂», «Н₃» - основи висот.

Висоти або їх продовження перетинаються в одній точці. Цю точку називають ортоцентром трикутника (на малюнках це точка «Н»).

Відношення висот у трикутнику є рівним оберненому відношенню сторін трикутника до яких ці висоти проведені.

Зобразимо наші висоти на малюнку:

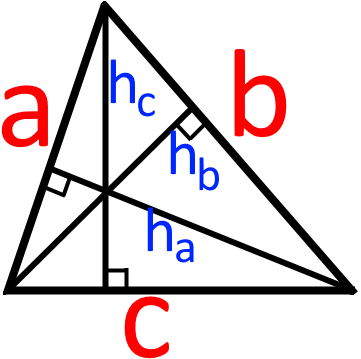
Тоді, дане правило можна записати так:

h_a : h_b : h_c = /1/a ∶ /1/b ∶ /1/c

Також, сума обернених довжин висот буде рівна оберненій довжині радіуса вписаного кола:

1h_a + 1h_b + 1h_c = /1/r

Види трикутників:

В залежності від довжини сторін розрізняють такі види трикутників: різносторонній, рівнобедрений, рівносторонній.

Різносторонній:

У різносторонньому трикутнику як слідує з назви довжини всіх сторін різні.

Рівнобедрений:

У рівнобедреного трикутника є дві рівні сторони. Рівні сторони рівнобедреного трикутника називають бічними сторонами, а його третю сторону – основою.

Властивість рівнобедреного трикутника:

Ознака рівнобедреного трикутника:

Рівносторонній:

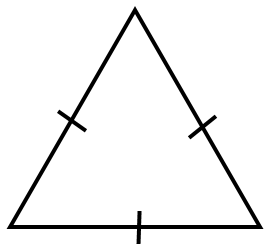
У рівностороннього трикутника всі сторони рівні.

Властивість рівностороннього трикутника:

Ознака рівностороннього трикутника: якщо в трикутнику всі кути рівні, то він рівносторонній.

В залежності від величини кутів розрізняють такі види трикутників: гострокутні, прямокутні, тупокутні.

Гострокутний:

У гострокутного трикутника всі кути гострі (їх градусна міра є меншою «90» градусів).

Прямокутний:

Прямокутний трикутник має один прямий кут (градусна міра одного з кутів рівна «90» градусів) і два гострих кути.

Сторона яка знаходиться навпроти прямого кута називається гіпотенузою, а дві інші сторони називають катетами.

Властивості прямокутного трикутника:

Тупокутний:

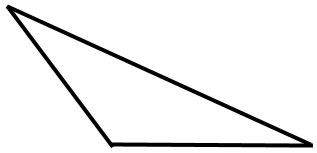
Тупокутний трикутник має один тупий кут (градусна міра одного з кутів більша «90» градусів) та два гострих кути.

Ознаки рівності трикутників:

Перша ознака рівності трикутників:

Друга ознака рівності трикутників:

Третя ознака рівності трикутників:

Подібні трикутники:

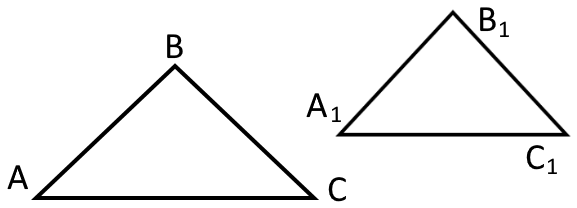
Трикутник «АВС» подібний до трикутника «А₁В₁С₁». Також слово «подібний» можна замінити символом «∼»:

∆ ABC ~ ∆ А₁В₁С₁

У подібних трикутників відповідні кути рівні, а відповідні сторони – пропорційні:

∠A = ∠A₁; ∠B = ∠B₁; ∠C = ∠C₁

Перша ознака подібності трикутників:

За двома сторонами та кутом між ними. Якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, утворені цими сторонами рівні, то такі трикутники є подібними.

Друга ознака подібності трикутників:

За трьома кутами. Якщо три кути (достатньо і двох кутів) одного трикутника відповідно дорівнюють двом кутам другого трикутника, то такі трикутники є подібними.

∠A = ∠A₁; ∠B = ∠B₁; ∠C = ∠C₁

Третя ознака подібності трикутників:

За трьома сторонами. Якщо три сторони одного трикутника пропорційні трьом сторонам другого трикутника, то такі трикутники є подібними.

Властивості подібних трикутників:

Відношення периметрів подібних трикутників дорівнює відношенню відповідних сторін і дорівнює коефіцієнту подібності:

Відношення площ подібних трикутників дорівнює квадрату коефіцієнта подібності:

Середня лінія трикутника. Теорема Фалеса

Середньою лінією трикутника називається відрізок, який сполучає середини двох його сторін.

Приклад: «MN» - середня лінія трикутника «АВС»

Середня лінія трикутника, яка сполучає середини двох даних сторін, паралельна третій стороні і дорівнює її половині.

Теорема Фалеса. Якщо паралельні прямі, що перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на іншій його стороні.

В умові теореми Фалеса замість сторін кута можна взяти дві довільні прямі.

Теорема про пропорційні відрізки. Паралельні прямі, що перетинають сторони кута, відтинають від сторін кута пропорційні відрізки.

Співвідношення у прямокутному трикутнику:

Якщо у прямокутному трикутнику «АВС», де кут «В» є прямим, провести висоту «ВН» до гіпотенузи «АС», то ми отримаємо два відрізки «АН» та «СН». Відрізок «АН» є проекцією катета «АВ» на гіпотенузу «АС», «СН» проекція катета «ВС» на гіпотенузу «АС».

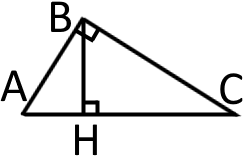
AC² = AB² + BC²

BH² = AH ∙ CH

AB² = AH ∙ AC

BC² = CH ∙ AC

BH = /AB · BC/AC

Тригонометричні співвідношення у прямокутному трикутнику

Найпростішими тригонометричними функціями є: «sin», «cos», «tg», «ctg». Давайте розберемося, що це за функції, як та коли їх використовувати.

В першу чергу необхідно розібратися, що вони роблять. Тригонометричні функції вказують на співвідношення чогось до чогось (кожна функція є унікальною) в залежності від заданого кута (значення). Сам кут (значення) може задаватися як у градусах так і в радіанах.

Щоб було зрозуміло про які співвідношення йде мова, розглянемо декілька прикладів:

Співвідношення у прямокутному трикутнику:

Наприклад «sin» кута «А» будемо шукати так: Беремо протилежний до нього катет (катет, що знаходиться навпроти нього) в нашому випадку це «ВС» та ділимо на гіпотенузу цього трикутника «АВ» (у прямокутному трикутнику гіпотенуза завжди знаходиться навпроти кута «90⁰» (прямого кута)). Тобто отримаємо: «sinA = /BC/AB»

	00	300	450	600	900
sin	0	/1/2	/√2/2 або /1/√2	/√3/2	1
cos	1	/√3/2	/√2/2 або /1/√2	/1/2	0
tg	0	/1/√3 або /√3/3	1	√3	-
ctg	-	√3	1	/1/√3 або /√3/3	0

Зауважимо, що тригонометричні функції можуть використовуватися не лише в прямокутниму трикутнику.

Детальніше про тригонометричну функцію, її властивості та базові формули ви можете прочитати тут.

Теорема синусів:

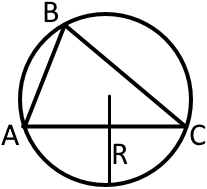
Теорему синусів можна сформулювати так:

Будь-яка сторона трикутника поділена на синус протилежного кута, буде рівна двом радіусам кола (діаметру) описаного навколо даного трикутника.

Тобто, ми можемо це записати так:

/AB/sin ⁡C = 2R; /BC/sin ⁡A = 2R; /AC/sin⁡ B = 2R

Врахувавши, що в кожній формулі права частина є однаковою («2R»), то ми можемо це об’єднати в один запис:

/AB/sin ⁡C = /BC/sin⁡ A = /AC/sin ⁡B = 2R

Під час використання даної теореми нам необхідно обрати будь-які дві частини з даної формули. Наприклад: «/BC/sin ⁡A = /AC/sin⁡ B» чи «/AB/sin ⁡C = 2R».

Теорему синусів використовують найчастіше тоді, коли необхідно об’єднати між собою дві сторони та два кути або сторону, кут та радіус описаного кола.

Теорема косинусів:

Теорему косинусів подібна до теореми Піфагора і її зручно запам’ятовувати так:

Сторона в квадраті є рівною сумі двох інших сторін в квадраті (це як шукати гіпотенузу в прямокутному трикутнику) відняти подвоєний добуток цих сторін (які додаються) на косинус кута між ними. Тобто, ми беремо кут який знаходиться навпроти сторони яка рівна цьому всьому.

Будемо вважати, що «a», «b», «c» - сторони трикутника, а «A», «B», «C» - кути трикутника.

Ось так можна записати:

a² = b² + c² - 2bc · cos⁡B

b² = a² + c² - 2ac · cos⁡A

c² = b² + c² - 2bc · cos⁡C

За допомогою цих формул можна шукати будь який кут трикутника. Для цього лише необхідно знати всі сторони цього трикутника.

Наприклад. Давайте знайдемо «cos B».

Для цього напишемо нашу формулу де використовується «cos B».

a² = b² + c² - 2bc · cos⁡B

Після чого перенесемо «cos B». та все, що з ним є у ліву частину, а все, що є у лівій частині перенесемо в праву. При цьому не забуваємо, що при перенесенні з однієї частини в іншу знак змінюється на протилежний. Отримаємо:

2bc · cos⁡B = b² + c² - a²

Після чого залишається лише розділити на все, що стоїть біля «cos B». В нашому випадку це «2bc». Отримаємо:

cosB = b² + c² - a²2bc

Після чого можна знайти і сам кут. Детальніше можете прочитати тут.

Також варто зауважити таку властивість:

Якщо «с» - найбільша сторона трикутника і

a² + b² > c², то кут С (кут, що навпроти найбільшої сторони) є гострим. Відповідно трикутник є гострокутним.

a² + b² = c², то кут С є прямим. Відповідно трикутник є прямокутним.

a² + b² < c², то кут С є тупим. Відповідно трикутник є тупокутним.

Коло, описане навколо трикутника:

Коло називають описаним навколо трикутника, якщо воно проходить через усі вершини трикутника. При цьому трикутник називають вписаним у коло.

Центром кола, описаного навколо трикутника, є точка перетину серединних перпендикулярів до його сторін.

Звідси випливає, що серединні перпендикуляри до сторін трикутника перетинаються в одній точці.

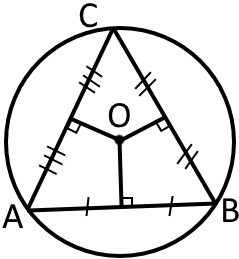
Центром кола, описаного навколо прямокутного трикутника, є середина його найбільшої сторони (гіпотенузи), а радіус кола дорівнює половині гіпотенузи.

Коло, вписане у трикутник:

Коло називається вписаним у трикутник, якщо воно дотикається до всіх його сторін. При цьому трикутник називається описаним навколо кола.

Центром кола, вписаного у трикутник, є точка перетину бісектрис цього трикутника (інцентр).