Графіки функцій
Для кращого розуміння даної теми, варто ознайомитися з прямокутною системою координат. Так ви можете зрозуміти як наносити точки на координатній площині.
Функція
З даною функцією ми вже ознайомилися тут.
Функцію яку можна задати формулою змінна, числа, називають лінійною. Число називається кутовим коефіцієнтом прямої. Число є координатою по «у» перетину графіку функції з віссю
Наведемо декілька прикладів лінійної функції: тощо.
Лінійна функція є визначеною на всій дійсній числовій множині.
Графіком лінійної є пряма. Для побудови графіка даної функції достатньо мати дві точки.
Для того щоб знайти точки через які проходить пряма, можна підставити будь-які числа замість змінної та знайти значення змінної На справді, в даній функції можна зробити і навпаки. Тобто, підставити значення замість змінної та знайти значення змінної Але, оскільки, таке можна робити далеко не у всіх функціях, то до такого краще не звикати.
Для запису результатів зручно використовувати таблицю:
| x | ||
| y |
У другу та третю колонку записують координати точок через які проходить графік функції.
Побудуємо графік функції
Отже, це у нас лінійна функція. Для її побудови достатньо мати дві точки через які проходить графік цієї функції. Візьмемо числа замість змінної та знайдемо значення змінної
Для першої точки візьмемо Отримаємо:
y = 2∙0 - 1
y = -1
Отже, перша точка через яку проходить графік функції має координати:
(0; -1)
Пам’ятаємо, що першим числом йде координата по осі а по осі Тобто:
(х; у)
Заповнимо нашу таблицю:
| x | 0 | |
| y | -1 |
Знайдемо координати другої точки. Візьмемо «х = 1». Отримаємо:
y=2 ∙1-1
y=2-1
y=1
Отже, друга точка матиме такі координати:
(1;1)
Заповнимо нашу таблицю:
| x | 0 | 1 |
| y | -1 | 1 |
Побудуємо графік нашої функції:

Коли ми будуємо графік функції за допомогою точок, то він виходить «точним». Якщо не має потреби будувати «точний» графік, а необхідно мати приблизний малюнок, то використовують ескіз.
Для побудови ескізу лінійної функції необхідно знати дві речі:
1. Точку перетину з віссю Це є значення
2. Нахил прямої. Це є значення
Якщо з точкою перетину із віссю все доволі просто. Яке число таку і точку перетину має функція з Мається, на увазі:
(0; b)
У функції маємо тому і точка перетину графіка функції з віссю була на увазі
Оскільки, є кутовим коефіцієнтом, то нахил прямої залежить від його знаку.
При лівий край прямої буде нижчий за правий. І дана пряма буде утворювати гострий кут із додатним напрямом осі та буде проходити з у чверть.
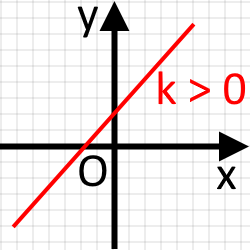
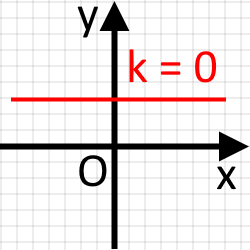
При пряма буде паралельною до осі І буде проходити через точку перетину графіка функції з віссю
При лівий край прямої буде вищий за правий. І дана пряма буде утворювати тупий кут із додатним напрямом осі та буде проходити з у чверть.

Якщо нашу функцію задано формулою де змінна, число крім нуля, то таку її називають прямою пропорційністю.
Функція «y = /k/x»
Враховуючи, що функцію називають прямою пропорційністю. То, функцію вигляду де змінна, число крім нуля, називають оберненою пропорційністю.
Областю допустимих значень функції є множина всіх дійсних чисел крім нуля. Це виникає через те, що при ми отримаємо ділення на нуль. Тому, необхідно викинути всі значення при яких наший знаменник перетвориться у нуль.
Дану точку змінної при якому знаменник перетворюється у називають точкою розриву.
Ось декілька виглядів даної функції: тощо.
Графіком даної функції є дві вітки гіперболи. Якщо то вітки будуть розташовані в та координатній чверті, а якщо то у та координатній чверті.
Ескізи даної функції виглядатимуть так:
При
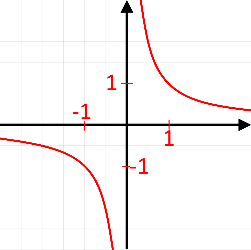
При

Для побудови «точного» графіка варто в першу чергу знайти значення при яких знаменник перетвориться у нуль. Після чого обирати наступні значення змінної відштовхуючись від цього значення (при якому знаменник рівний нулеві), тобто брати числа ліворуч та праворуч від цього значення. Для побудови графіка даної функції варто мати хоча б по три числа (по три точки) з кожної сторони (ліворуч та праворуч). Для запису координат точок також будемо використовувати таблицю.
Побудуємо графік функції
В першу чергу знайдемо значення змінної при якому знаменник буде перетворюватися в нуль та викинемо це значення. Тобто, ми знайдемо ОДЗ даної функції. Матимемо:
x - 2 ≠ 0
x ≠ 2
Отже, змінна не може набувати значення Тому, наше ОДЗ буде таким:
D(y) =
Тепер ми можемо скласти таблицю. Для змінної будемо обирати числа, що знаходяться ліворуч та праворуч від числа Візьмемо по три значення з кожної сторони.
Пам’ятаємо, що нам необхідно підставити замість змінної обране число та знайти значення змінної
Тут є не велика хитрість. Якщо обирати числа замість які є рівновіддалені від числа при якому знаменник перетвориться у нуль нашому випадку це то будемо мати однакові значення але з протилежним знаком.
| x | 0 | 1 | 1,5 | 2,5 | 3 | 4 |
| y | -0,5 | -1 | -2 | 2 | 1 | 0,5 |
Побудуємо графік нашої функції. В точці проведемо пряму. Як помітно графік до неї наближається але не перетинає її.

Функція
Областю допустимих значень функцій та є множина всіх дійсних чисел. Графіком даних функції є парабола.
Розглянемо функцію її вітки направлені вгору, а вершина параболи знаходиться в початку координат точці

Розглянемо функцію Напрямок віток параболи даної функції залежить від коефіцієнта Якщо додатне то вітки параболи будуть направлені вгору. Якщо від’ємне
Вершину параболи ми можемо позначити як:
(x0; y0)
Координату вершини параболи по осі можна знайти так:
x0 = -/b/2a
Координату вершини параболи по осі можна знайти підставивши значення замість у виразі Матимемо:
y0 = ax02 + bx0 + c
Цього цілком достатньо щоб побудувати ескіз графіка функцій. Для того щоб побудувати «точний» графік необхідно взяти хоча б по точки ліворуч та праворуч від вершини параболи. Ще часто шукають точки перетину з віссю розв’язуючи при цьому рівняння
Побудуємо графік функції
В першу чергу визначимо напрямок віток параболи. Оскільки, коефіцієнт тобто є від’ємним то вітки параболи будуть направлені вниз.
Тепер визначимо координати вершини параболи
Знайдемо координату по осі за допомогою формули:
x0 = -/b/2a
Матимемо:
x0 = -/6/2 ∙ (-1) = 3
Знайдемо координату по осі за допомогою формули:
y0 = ax02 + bx0 + c
Матимемо:
y0 = -32 + 6∙3 - 5
y0 = 4
Отже, вершина параболи має координати:
(3; 4)
Тепер знайдемо декілька точок які належать графіку функції. Візьмемо декілька значень змінної Краще за все обирати значення ліворуч та праворуч від координати вершини параболи по осі відносно числа
В даному випадку, якщо обирати числа рівновіддалені від вершини параболи по осі то значення по осі будуть однаковими.
Складемо таблицю.
| x | 1 | 2 | 3 | 4 | 5 |
| y | 0 | 3 | 4 | 3 | 0 |
Побудуємо графік функції:
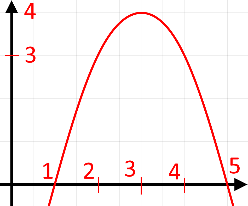
Функція
Областю допустимих значень функції невід’ємних чисел. В нашому випадку це Тобто, щоб знайти область допустимих значень нам необхідно написати, що підкореневий вираз є за нуль. Після чого розв’язати отриману нерівність.
Графіком функції є вітка параболи.
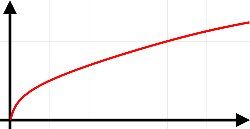
Для того щоб побудувати даний графік можна обирати значення з області допустимих значень або з першу розв’язати рівняння «підкореневий вираз дорівнює нулю» після чого обирати ті значення замість змінної при яких підкореневий вираз буде додатнім.
Побудуємо графік функції
Для побудови графіка функції нам варто розв’язати нерівність:
x + 2 ≥ 0
В такий спосіб ми знайдемо ОДЗ. Пам’ятаємо, що під коренем парного степеня не може знаходитися від’ємне число. Отже, будемо мати:
x ≥ -2
Матимемо ОДЗ:
D(y) ∈ [-2; +∞)
Для побудови графіка функції нам варто використовувати значення, що належать ОДЗ.
Для зручності скористаємося таблицею.
| x | -2 | -1 | 2 |
| y | 0 | 1 | 2 |
Побудуємо графік даної функції.
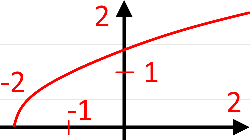
Степенева функція
Функцію виду число, називають степеневою. В залежності від того яким є число «a» ми будемо мати різні графіки та властивості даної функції.
Розглянемо різні варіанти.
Якщо тоді наша функція матиме такий вигляд:
Тобто:
y = 1
При цьому дана функція матиме точку розриву при адже в такому випадку матимемо:
y = 00
І графік нашої функції буде пряма яка є паралельною до осі (перпендикулярною до осі і проходить через координату по осі точку
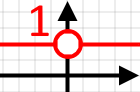
Якщо у нас є функція то пряма буде проходити через координату по осі (через точку
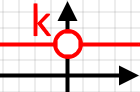
Якщо тоді наша функція матиме такий вигляд:
Тобто:
y = x
Отже, при ми будемо мати лінійну функцію яку розглядали раніше.
Якщо тоді наша функція матиме такий вигляд:
Отже, при ми будемо мати квадратну функцію яку розглядали раніше.
Якщо парне натуральне число то графіком даної функції буде парабола:

Якщо непарне натуральне число то графіком даної функції буде таким:

Якщо не ціле додатне число то функція є визначеною на проміжку
Якщо то графік функції буде мати вигляд:
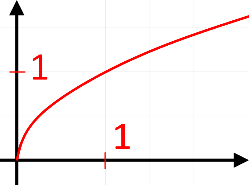
Якщо то графік функції буде мати вигляд:

Якщо не ціле від’ємне число то функція є визначеною на проміжку
Якщо то графік функції буде мати вигляд: