Простий рух тіла

В першу чергу нам потрібно розібратися із позначеннями. Наші величини будемо позначати так:

Деколи доведеться зустрічатися з таким поняттям як «середня швидкість». Для того, щоб знайти значення середньої швидкості вам необхідно всю відстань пройдену тілом поділити на весь затрачений час.

Також, напишемо їх одиниці вимірювання. Для швидкості це «км/год» (кілометри за годину) або «м/с» (метри за секунду), відстані – «км» (кілометри) або «м» (метри), часу – «год» (години) або «с» (секунди).

Одиниці вимірювання є важливими. Адже, при розв’язуванні задач вам необхідно зробити так, щоб величини (швидкість, відстань, час) були в однакових одиницях. Для цього їх часто доводиться «переводити» (перетворювати). Детальніше про одиниці вимірювання та їх перетворення читайте тут.

Зазвичай, задачі на швидкість, відстань, час можна розв’язати за допомогою «трикутника». Цей «трикутник» виглядає так:

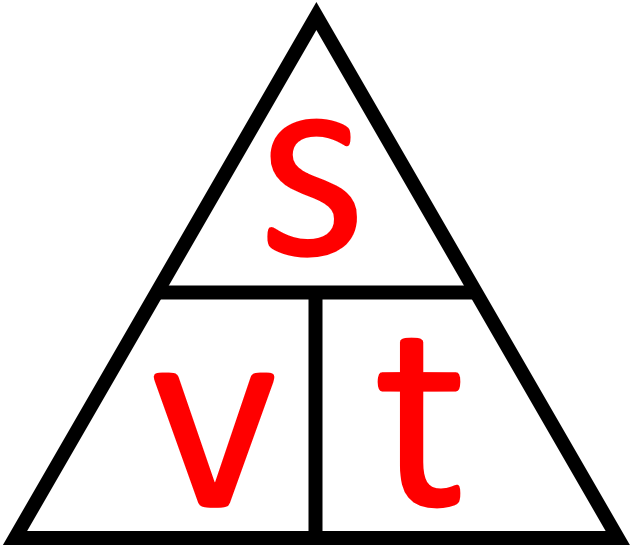
З ним працювати доволі просто. Коли нам необхідно знайти якусь величину, то ми її «закриваємо» і дивимось на те що залишилося.

Якщо дві величини знаходяться на одному рівні (в одному рядку), то це означає, що вони між собою множаться.

Якщо дві величини знаходяться на різних рівнях (одна в горі інша з низу), то це означає, що верхню величину потрібно поділити на нижню.

Також, багато таких задач зручно розв’язувати за допомогою лінійних рівнянь.

Розв’яжемо наступну задачу: Велосипедист їхав зі швидкістю «12 км/год». Він проїхав «48 км». Скільки годин рухався велосипедист?

В даній задачі ми маємо такі речення «їхав зі ШВИДКІСТЮ 12 км/год», тобто, нам відома швидкість «v = 12 км/год». А, також, «він проїхав 48 км», тобто, нам відома відстань «s = 48 км». Також, ви можете орієнтуватися на одиниці вимірювання. Тобто, на «км/год» та «км». Враховуючи, що в обох величинах використовуються кілометри (км), то це означає, що нам не потрібно нічого перетворювати (переводити одиниці вимірювання).

Виходить, що нам необхідно знайти час «t».

Отже, розглянемо ще раз наш трикутник:

Враховуючи, що потрібно знайти час («t»), то ми закриваємо «t»:

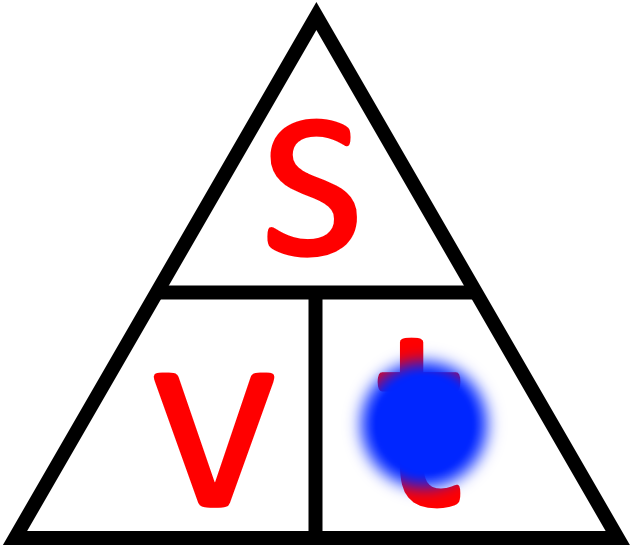
Як помітно у нас залишилась «s» над «v». Це означає, щоб знайти час нам потрібно відстань поділити на швидкість (верх ділимо на низ). Тобто:

t = s ∶ v

Підставимо наші числа та отримаємо:

t = 48 ∶ 12

t = 4

Враховуючи, що швидкість вимірювалася в «км/год», то будемо мати, що час записують через «год». Отже:

t = 4 год

Розглянемо ще задачі на знаходження середньої швидкості тіла

Задача: Велосипедист за першу годину проїхав «10 км», а за дві наступні «26 км». Знайти середню швидкість руху велосипедиста.

Для того, щоб знайти середню швидкість велосипедиста нам необхідно всю відстань розділити на весь час.

Оскільки, велосипедист з першу проїхав «10 км», а потім «26 км», то загальна відстань буде:

s = 10 + 26

s = 36

Тепер, знайдемо весь час. За умовою задачі сказано, що він їхав з першу «1 годину», а потім ще «2 години». Тому, загальний час буде:

t = 1 + 2

t = 3

Отже, щоб знайти середню швидкість («v_c») нам необхідно всю відстань розділити на весь час. Будемо мати:

v_c = s ∶ t

v_c = 36 ∶ 3

v_c = 12

Виходить, що середня швидкість велосипедиста буде «12 км/год».

Рух тіла за/проти

Доволі часто зустрічаються задачі в яких доводиться враховувати додаткову швидкість. Наприклад, коли є рух «за» течією/вітром або «проти» течії/вітру. В таких ситуаціях вам необхідно шукати «кінцеву» швидкість.

Якщо тіло рухається «за» течією/вітром, то його «кінцева» швидкість буде сумою (додавання) швидкості тіла та течії/вітру.

Якщо тіло рухається «проти» течії/вітру, то його «кінцева» швидкість буде різницею (віднімання) швидкості тіла та течії/вітру.

Розглянемо таку задачу: Човен пливе проти течії. Швидкість човна «12 км/год», а швидкість течії «5 км/год». Скільки кілометрів пропливе човен за «3 год»?

В даній задачі нам відома швидкість човна «12 км/год». Позначимо це як «v_ч» («v_ч = 12 км/год»). Також, нам відома швидкість течії «5 км/год». Позначимо це як «v_т» («v_т = 5 км/год»). Цей човен плив «3 год», тобто ми маємо час («t = 3 год»). І нам необхідно знайти відстань («s = ?»).

Враховуючи, що човен рухається проти течії, то щоб знайти його «кінцеву» швидкість («v») потрібно від швидкості човна відняти швидкість течії.

v = v_ч - v_т

Будемо мати:

v = 12 - 5

v = 7 км/год

Скориставшись «трикутником» (тобто, «закриваємо s») ми побачимо, що для того, щоб знайти відстань потрібно швидкість помножити на час (бо «v» та «t» знаходяться на одному рівні). Отже:

s = v ∙ t

Підставимо числа:

s = 7 ∙ 3

s = 21 км

Отже, човен пропливе «21 км».

Розглянемо приклад схожої задачі, але з використанням лінійних рівнянь.

Задача: Велосипедист рухається зі швидкістю «11 км/год». Він їде за вітром. За дві години він проїхав «28 км». Знайдіть швидкість вітру.

Розберемо яку інформацію нам відомо з умови задачі.

Нам відома швидкість велосипедиста «11 км/год». Напишемо це так: «v_вел = 11 км/год». Відомо, що велосипедист рухався протягом «2 год» («t = 2 год») і за цей час він проїхав «28 км» («s = 28 км»). Нам потрібно знайти швидкість вітру. Напишемо це так: «v_віт = ?».

За умовою задачі велосипедист рухається за вітром. Тобто, вітер дує йому в спину тим самим буде допомагати при русі.

В такій ситуації кінцева швидкість («v») це буде сума швидкості велосипедиста та вітру («v = v_вел + v_віт» або «v_вел + v_віт = v»).

Оскільки, під час руху в нас буде використовуватися саме кінцева швидкість і ми маємо відстань та час, то можемо спробувати її (значення кінцевої швидкості) знайти. Скориставшись трикутником ми побачимо, що для знаходження швидкості потрібно відстань поділити на час.

v = s ∶ t

Підставимо значення та отримаємо:

v = 28 ∶ 2

v = 14

Отже, кінцева швидкість буде «14 км/год» («км/год», бо у нас відстань є в «км», а час в «год»).

Ми отримали кінцеву швидкість. Тепер, нам варто знайти швидкість вітру. А, швидкість вітру використовується в рівнянні «v_вел + v_віт = v». Підставимо все, що нам є відомим:

11 + v_віт = 14

Якщо замінити «v_віт» на «х» («v_віт = х»), то ви отримаєте лінійне рівняння у звичному вигляді (у нас і так є лінійне рівняння, але багато хто звик, що там має бути «х». Але яку б ви букву не використовували сенс залишиться таким же).

11 + х = 14

х = 14 – 11

х = 3

v_віт = 3 км/год

Отже, швидкість вітру буде «3 км/год».

Задачі, коли два тіла рухаються один за одним (одне тіло «втікає» від іншого або «наздоганяє» інше)

Мабуть, у кожного в житті були ситуації, коли доводилося спостерігати як якась людина «доганяє» іншу (або «втікає» від когось). Багатьом доводилося й самим бути в ролі «наздоганяючого» («втікаючого»).

Дану ситуацію можна показати у вигляді такої схеми:

Як бачите «тіло 2» рухається за «тілом 1» (наздоганяє). При цьому «тіло 2» зможе наздогнати «тіло 1» лише за умови, що його швидкість буде більшою («v₂ > v₁» ситуація коли «наздоганяємо»), а «тіло 1» може «втекти» від «тіла 2» лише, коли його швидкість буде більшою («v₁ > v₂» ситуація, коли «втікаємо»).

При цьому, коли маємо задачу про «наздоганяючого», то щоб знайти «кінцеву» швидкість потрібно від «v₂» (наздоганяючого) відняти «v₁» (втікаючого).

v = v₂ - v₁

Якщо кінцева швидкість вийде від’ємною, то наздогнати тіло не вдасться, а якщо додатною, то наздогнати вдасться. Зауважимо, що багато задач не використовують «кінцеву» швидкість. Вона скоріше необхідна для перевірки чи вдасться наздогнати.

А, коли задача про «втікаючого», то потрібно від «втікаючого» відняти «наздоганяючого».

v = v₁ - v₂

Не хвилюйтеся, якщо ви заплутались. На практиці все доволі просто. І щоб знайти «кінцеву» швидкість достатньо від більшої швидкості відняти меншу. Головне, щоб ви не заплутались з тим що робити далі

Розглянемо декілька задач.

Задача 1 (на віддалення): З міста «А» до міста «Б» вийшов пішохід зі швидкістю «4 км/год» та виїхав велосипедист зі швидкістю «7 км/год». Через скільки часу відстань між велосипедистом та пішоходом буде «6 км»?

Враховуючи, що в даній задачі ми маємо дві швидкості, то краще відразу їх якось відрізняти. Для прикладу будемо швидкість пішохода позначати як «v_п», а велосипедиста як «v_в». Тоді, матимемо, що «v_п = 4 км/год» і «v_в = 7 км/год».

Початок цієї задачі ми можемо показати у вигляді такого малюнку:

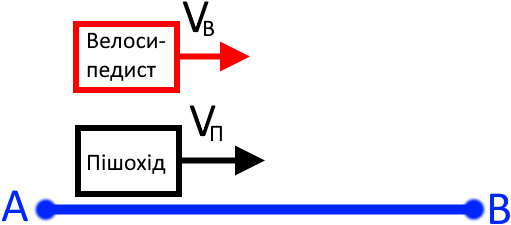
Враховуючи, що швидкість велосипедиста є більшою за швидкість пішохода, то через деякий час наші тіла на малюнку виглядатимуть так:

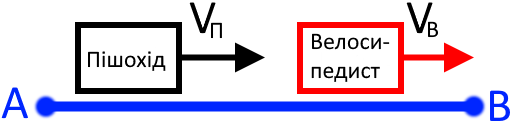
Як бачите, між ними утворилася відстань «s». Нам необхідно знайти час через який ця відстань буде «6 км» («s = 6 км»).

Для цього, в першу чергу, необхідно знайти різницю їх швидкостей Тобто, «кінцеву» швидкість. Позначимо її як «v». Оскільки, швидкість велосипедиста є більшою, то від неї будемо віднімати швидкість пішохода.

v = v_в - v_п

v = 7 - 4

v = 3 км/год

Ми маємо швидкість («3 км/год»), також нам відома відстань («6 км») і нам необхідно знайти час. Скориставшись трикутником величин ми побачимо, що щоб знайти час потрібно відстань поділити на швидкість:

t = s ∶ v

t = 6 ∶ 3

t = 2 год

Отже, велосипедист та пішохід будуть на відстані «6 км» один від одного через «2 год» після початку руху.

Задача 2 (на наздоганяння): З міста «А» виїхав велосипедист зі швидкістю «12 км/год», а через «30 хвилин» виїхав другий велосипедист зі швидкістю «15 км/год». Через скільки часу вони зустрінуться?

Розберімося як взагалі все відбувається. Виходить, що перший велосипедист почав рухатися з міста «А» та їхав протягом «30 хвилин». Після чого, з того ж самого міста «А» слідом (навздогін) виїде другий велосипедист. Це можна намалювати так:

Через певний проміжок часу вони зустрінуться. Це можна показати у вигляді такого малюнку:

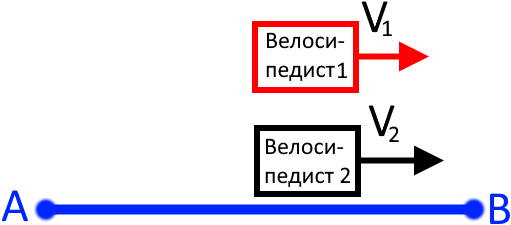
Зверніть увагу, що обидва велосипедисти подолають однакову відстань. Від міста «А» до точки їх зустрічі «В».

Дуже часто в таких задачах діє принцип «відоме, необхідно знайти, не відоме». І щоб розв’язати такі задачі потрібно «позбутися» від «не відомого». Зазвичай (мова йде про прості завдання) «не відоме» можна зробити (або воно відразу буде) спільним для обох об’єктів (тих хто рухається).

Для прикладу, розберемося, що в нашій задачі є «відомим», «необхідно знайти» і «не відоме».

Очевидно, що «відомим» є швидкість. Адже, по факту лише вона одна є чітко вказана (в деяких моментах «відоме» ми можемо знайти із задачі). В задачі нас просять знайти через який час вони зустрінуться, отже «необхідно знайти» саме час зустрічі. І «не відомим» є відстань від якої нам необхідно позбутися.

Для початку давайте все якось позначимо. Швидкість першого велосипедиста напишемо як «v₁», а другого «v₂». Враховуючи, що швидкість є відомою, то її можемо записати «v₁ = 12 км/год» і «v₂=15 км/год». Відстань від міста «А» до точки зустрічі «В» позначимо як «s», а час через який відбулась зустріч «t».

Також, зауважимо, що час руху другого велосипедиста («t₂») буде таким же, як час до моменту зустрічі «t₂ = t», а час руху першого велосипедиста («t₁») буде на «30 хв» більшим, адже він почав рухатися раніше «t₁ = t + 30 хв».

Оскільки швидкість записана у годинах, то і час потрібно вказувати у годинах. Для того, щоб хвилини перетворити у години потрібно їх поділити на «60». Отже: «30 хв = /30/60; год = /1/2; год = 0,5 год».

Зауважимо, що для обох велосипедистів відстань є однаковою. Тому, можемо спробувати записати її для кожного велосипедиста.

Щоб знайти відстань ми можемо скористатися нашим трикутником:

s = v ∙ t

Врахувавши значення швидкості та часу першого велосипедиста будемо мати:

s = v₁ ∙ t₁

s = 12 ∙ (t + 0,5)

А, для другого:

s = v₂ ∙ t₂

s = 15 ∙ t

Зверніть увагу, в кожному рівнянні у лівій частині ми маємо «s». Якщо, у двох рівняннях є однакові частини, то це означає, що інші частини також є однаковими. Тому, ми можемо записати так (порядок обираєте самостійно):

15 ∙ t = 12 ∙(t + 0,5)

Ми отримали лінійне рівняння. Розв’яжемо його.

15t = 12t + 6

15t - 12t = 6

3t = 6

t = 6 ∶ 3

t = 2

Виходить, що наші велосипедисти зустрінуться через «2 години».

Рух тіл в одному/протилежних напрямках

Часто бувають ситуації, коли два тіла рухаються один на зустріч одному (для прикладу коли ви вирішили зустрітися в якомусь місці і йдете до цього місця з різних сторін) або ж рухаються з одного місця у протилежні напрямки (коли після зустрічі з друзями ви йдете до дому в протилежних напрямках).

Рух на зустріч один одному можна зобразити так:

Рух у протилежних напрямках можна зобразити так:

В таких випадках ми маємо «швидкість зближення», коли тіла рухаються на зустріч один одному або «швидкість віддалення», коли тіла рухаються у протилежних напрямках. Цю швидкість можна знайти як суму швидкостей обох тіл:

v = v₁ + v₂

Якщо почали рух одночасно і рухались без перерв, то час руху для обох тіл буде однаковим.

І тоді дані тіла можна розглядати як одне тіло, яке рухається з даною швидкістю («v»).

А, відстань, яку подолає єдине тіло буде рівна сумі відстаней, яку подолає кожне з тіл окремо:

s = s₁ + s₂

Розглянемо декілька задач.

Задача 1 (рух на зустріч): З міста «А» та «В» на зустріч один одному виїхали автомобіль і мотоцикліст. Через скільки годин вони зустрінуться, якщо швидкість автомобіля «70 км/год», а мотоцикліста «50 км/год». А, відстань між містами «480 км».

Для нашої зручності виконаємо малюнок, який буде демонструвати нашу задачу.

В даній задачі матимемо, що швидкість автомобіля є «70 км/год» і ми зможемо це записати як «v_A = 70 км/год», а швидкість мотоцикла є «50 км/год», і напишемо це як «v_M = 50 км/год». Відстань між містами «А» та «В» є «480 км» і ми можемо це записати як «s = 480 км». Нам необхідно знайти час зустрічі «t = ?».

Враховуючи, що наші тіла рухаються один навпроти одного, то ми можемо їх «об’єднати» в одне тіло і розв’язувати задачу відносно цього тіла. Дане тіло буде мати швидкість «зближення» яка складається з суми швидкостей автомобіля та мотоцикліста. Напишемо дану швидкість як «v», матимемо:

v = v_A + v_M

v = 70 + 50

v = 120

Загальна швидкість буде «v = 120 км/год».

В такій ситуації час можна знайти за допомогою нашого трикутника. Отже, формула буде:

t = s ∶ v

Підставимо наші числа:

t = 480 ∶ 120

t = 4

Автомобіль та мотоцикліст зустрінуться через «4 год» від початку руху.

Задача 2 (рух в протилежних напрямках): Андрій та Степан грали в теніс. Після гри кожен з хлопців пішов додому. Вони жили в протилежних сторонах. На якій відстані вони будуть один від одного через «12 хвилин», якщо Андрій йшов зі швидкістю «47 м/хв», а Степан – «54 м/хв»?

Для нашої зручності виконаємо малюнок, який буде демонструвати нашу задачу.

В даній задачі матимемо, що швидкість Андрія є «47 м/хв» і ми зможемо це записати як «v_A = 47 м/хв», а швидкість Степана є «54 м/хв», і напишемо це як «v_С = 54 м/хв». Час протягом якого вони рухались є «12 хв» і ми можемо це записати як «t = 12 хв». Нам необхідно знайти відстань яку вони пройдуть за даний час «s = ?».

Враховуючи, що наші тіла рухаються в протилежних напрямках один від одного, то ми можемо їх «об’єднати» в одне тіло і розв’язувати задачу відносно цього тіла. Дане тіло буде мати швидкість «віддалення» яка складається з суми швидкостей Андрія та Степана. Напишемо дану швидкість як «v», матимемо:

v = v_A + v_С

v = 47 + 54

v = 101

Загальна швидкість буде «v = 101 м/хв».

В такій ситуації відстань можна знайти за допомогою нашого трикутника. Отже, формула буде:

s = v ∙ t

Підставимо наші числа:

s = 101 ∙ 12

s = 1212

Андрій та Степан через «12 хвилин» будуть на відстані «1212 метрів» один від одного.