Для того, щоб правильно розв’язувати рівняння з модулем вам варто пригадати такі теми як лінійні рівняння, квадратні рівняння, рівняння з модулем.

Коли ви розв’язуєте рівняння з модулем, то вам варто звести дане рівняння до базового вигляду. Щоб визначити тип рівняння варто подивитися на кількість модулів в рівнянні та на вираз який знаходиться за межами модуля.

Також пам’ятайте про обмеження модуля. Модуль не може бути рівний від’ємному числу!

1) Розв’язати рівняння «|x² - 3x + 2| - 2 = 0».

Звернемо увагу, що в нас є один єдиний модуль. В такій ситуації потрібно звести до стандартного вигляду «модуль = все інше». Тобто, потрібно перенести «- 2» з лівої частини в праву (не забуваємо змінити знак на протилежний):

|x² - 3x + 2| = 2

Враховуючи, що модуль рівний числу, то ми маємо такий тип рівняння «|f(x)| = a». При цьому, якщо число «a» є більшим за нуль («a > 0»), то таке рівняння має два розв’язки:

f(x) = a

f(x) = -a

Отже, в нашому випадку ми отримаємо два рівняння:

x² - 3x + 2 = 2

x² - 3x + 2 = -2

Розв’яжемо перше рівняння.

x² - 3x + 2 = 2

Враховуючи, що максимальним степенем не відомої є «2» («x²»). То, це є квадратне рівняння. Зведемо все до стандартного вигляду (перенесемо все в одну частину і прирівняємо до нуля):

x² - 3x + 2 - 2 = 0

x² - 3x = 0

Отримали не повне квадратне рівняння.

x(x - 3) = 0

x = 0; x - 3 = 0

x = 0; x = 3

Отже, розв’язками першого рівняння є «0» та «3». Розв’яжемо друге рівняння.

x² - 3x + 2 = -2

x² - 3x + 2 + 2 = 0

x² - 3x + 4 = 0

Це є повне квадратне рівняння. Скористаємось дискримінантом:

D = (-3)² - 4 ∙ 1 ∙ 4 = 9 - 16 = -7

Враховуючи, що дискримінант є від’ємним, то дане рівняння розв’язків не має. Тому, розв’язками початкового рівняння є «0» та «3».

Відповідь: 0; 3.

2) Розв’язати рівняння «-3|5 - 2x| - 21 = 0».

Маємо єдиний модуль. Зведемо дане рівняння до стандартного вигляду «модуль = все інше».

-3|5 - 2x| - 21 = 0

-3|5 - 2x| = 21 |∶(-3)

|5 - 2x| = -7

Пам’ятаємо, що модуль не може бути рівний від’ємному числу, тому дане рівняння розв’язків не має.

x ∈ ∅

Відповідь: ∅.

3) Розв’язати рівняння «|(|x + 2| - 1)| = 4».

В даному рівнянні ми маємо декілька модулів, але враховуючи, що один модуль знаходиться в середині іншого, то можна сказати що ми маємо лише один модуль. Бо всю внутрішню частину великого модуля («|x + 2| - 1») можна вважати як одне ціле. Тому, ми маємо звичайне рівняння «модуль = число». Отже, розкривши зовнішній модуль будемо мати два рівняння.

Перше:

|x + 2| - 1 = 4

Друге:

|x + 2| - 1 = -4

Розв’яжемо кожне з даних рівнянь. Розпочнемо з першого:

|x + 2| - 1 = 4

Зведемо його до базового вигляду «модуль = все інше»:

|x + 2| = 1 + 4

|x + 2| = 5

Отримали знову просте рівняння з модулем. Розкривши модуль знову отримаємо два рівняння:

x + 2 = 5; x + 2 = -5

x = 5 - 2; x = -5 - 2

x = 3; x = -7

Отже, отримали два розв’язки «3» і «- 7».

Розглянемо друге рівняння:

|x + 2| - 1 = -4

|x + 2| = -4 + 1

|x + 2| = -3

Оскільки, модуль не може бути рівний від’ємному числу, то дане рівняння не має розв’язків.

Відповідь: 3; -7.

4) Розв’язати рівняння «|3x² - x| = 8 + x».

Враховуючи, що ми маємо один єдиний модуль, то варто написати його в базовому вигляді «модуль = все інше». В нашому випадку це вже є написаним. Оскільки, модуль рівний виразу в якому є «х», то таке рівняння ми мусимо розв’язати після чого перевірити чи наші розв’язки допускаються ОДЗ.

Пам’ятаємо, що модуль не може бути рівний від’ємному числу. Тому, права частина (якій рівний модуль) має бути більша-рівна за нуль:

8 + x ≥ 0

x ≥ -8

Якщо ви не хочете розв’язувати нерівність, то можна розв’язки рівняння в кінці підставити в праву частину (в такому випадку в «8 + x») і подивитися на результат. Якщо він додатній або нуль, то даний розв’язок вам підходить. Якщо від’ємний, то розв’язок не підходить.

Даний тип рівняння має вигляд:

|f(x)| = g(x)

А, його розв’язками будуть такі рівняння:

f(x) = g(x)

f(x) = -g(x)

Тобто, ми матимемо перше рівняння:

3x² - x = 8 + x

Друге:

3x² - x = -(8 + x)

Почнемо з першого рівняння.

3x² - x = 8 + x

Перенесемо все в одну частину:

3x² - x - 8 - x = 0

3x² - 2x - 8 = 0

Отримали квадратне рівняння розв’язками якого будуть числа:

x₁ = 2; x₂ = -/4/3

Зауважимо, що обидва числа входять в ОДЗ («x ≥ -8»). Тому, вони обидва є розв’язками початкового рівняння.

Розв’яжемо друге рівняння.

3x² - x = -(8 + x)

3x² - x + 8 + x = 0

3x² + 8 = 0

3x² = -8

x² = -/8/3

Це є не повне квадратне рівняння. Враховуючи, що «x²» не може бути рівний від’ємному числу, то дане рівняння розв’язків не має.

x ∈ ∅

Відповідь: 2; -/4/3.

5) Розв’язати рівняння «x² - 7|x| + 10 = 0».

Зверніть свою увагу, що ми маємо лише один єдиний корінь. Тому, можна припустити, що це є рівняння типу «|f(x)| = g(x)» (оскільки за межами кореня є «х»). Але враховуючи, що в нас є «x²», то можна скористатися властивістю парного степеня. Тобто, що будь-яке число в парному степені буде більшим-рівним за нуль. Таку ж саму властивість має і корінь. Тому, ми можемо «x²» написати як «|x|²». Після чого наше рівняння буде мати вигляд:

|x|² - 7|x| + 10 = 0

Зверніть свою увагу, що наші корені є абсолютно однаковими та змінна «х» знаходиться лише там. Тому, ми можемо виконати заміну змінної та розв’язати спрощене рівняння.

Заміна:

t = |x|

Спрощене рівняння:

t² - 7t + 10 = 0

Отримали повне квадратне рівняння розв’язками якого будуть:

t₁ = 2; t₂ = 5

Тепер нам варто повернутися до заміни.

При «t = 2»:

|x| = 2

Це є найпростіше рівняння з модулем типу «|f(x)| = a», де «a > 0». Отже, матимемо розв’язки:

x₁ = 2; x₂ = -2

При «t = 5»:

|x| = 5

x₃ = 5; x₄ = -5

Відповідь: -5; -2; 2; 5.

6) Обчислити «x ∙ y», якщо «|y - 1| + x² - 2xy + y² = 0».

В даному рівнянні ми маємо дві не відомі («х» та «у»), тому дане рівняння розв’язати в лоб не можливо (бо кількість змінних/не відомих є більшою за кількість рівнянь). Тому, доведеться скористатися якимись хитростями.

Зверніть свою увагу на вираз «x² - 2xy + y²». На справді це є формула скороченого множення. Тому, ми можемо виконати такі перетворення:

x² - 2xy + y² = (x - y)²

Отже, наше рівняння буде мати вигляд:

|y - 1| + (x - y)² = 0

Зауважимо, що вирази «|y - 1|» та «(x - y)²» є більшими-рівними за нуль, тобто не можуть набувати від’ємних значень. Але їх сума є рівною нулеві. Таке можливо лише, якщо обидва вирази будуть рівні нулеві одночасно. Тобто:

y - 1 = 0; x - y = 0

Отже, нам необхідно прирівняти кожен вираз до нуля і знайти їх спільний розв’язок. Це можна зробити за допомогою системи рівнянь.

{/y - 1 = 0/x - y = 0

{/y = 1/x = y

{/y = 1/x = 1

Отже, матимемо:

x ∙ y = 1 ∙ 1 = 1

Відповідь: 1.

7) Розв’язати рівняння «|x² - x + 1| = |x² - 3x + 4|».

В даному рівнянні ми маємо ситуацію, коли корінь рівний кореню. Це є тип рівняння «|f(x)| = |g(x)|».

Даний тип має декілька способів розв’язання.

Перший спосіб полягає в тому, що нам варто замінити модуль на парний степінь (на квадрат). Тобто, саме рівняння набуде такого вигляду:

|f(x)| = |g(x)|

[f(x)]² = [g(x)]²

В нашому випадку це виглядатиме так:

(x² - x + 1)² = (x² - 3x + 4)²

Після чого ви можете скористатися формулами скороченого множення та відкрити дужки, або перенести це все в одну частину і також скористатися формулою скороченого множення («a² - b²»).

Даний метод зазвичай використовується, якщо ви маєте нерівності.

Другий спосіб вважається «розписаним» (кінцевим варіантом) першого способу. Використовуючи цей спосіб ви відразу забираєте модуль та отримуєте два рівняння. В першому рівнянні ви обираєте однакові знаки для обох модулів, а в другому рівнянні протилежні знаки. Це виглядатиме так:

|f(x)| = |g(x)|

{/± f(x) = ± g(x)/± f(x) = ∓ g(x)

В нашому випадку можна взяти перше рівняння зі знаками «+», а друге рівняння ліву частину зі знаком «+», а праву – «-». Матимемо:

Перше рівняння:

x² - x + 1 = x² - 3x + 4

Друге рівняння:

x² - x + 1 = -(x² - 3x + 4)

Інші методи не розглядаємо, бо вони часто бувають складнішими чим два базові методи.

Скористаємося другим способом і почнемо з розв’язування першого рівняння.

x² - x + 1 = x² - 3x + 4

x² - x + 1 - x² + 3x - 4 = 0

2x - 3 = 0

x = 3∶2

x = 1,5

Друге рівняння:

x² - x + 1 = -(x² - 3x + 4)

Ми можемо не розкривати дужки в правій частині, а відразу перенести її в ліву. При перенесені правої частини в ліву в нас поміняється ЛИШЕ знак перед дужками з «-» на «+», тому ці дужки можна буде відразу забрати. Матимемо:

x² - x + 1 + x² - 3x + 4 = 0

2x² - 4x + 5 = 0

Отримали повне квадратне рівняння.

D = (-4)² - 4∙2∙5 = 16 - 40 = -24

Враховуючи, що дискримінант вийшов меншим за нуль (від’ємним), то дане рівняння не має розв’язків.

Відповідь: 1,5.

8) Розв’язати рівняння «|x² - 4x + 3| + |x² - 5x + 6| = 1».

Як бачите, у нас є декілька модулів. При цьому є вираз без модуля. Тому, дане рівняння має тип «|f(x)| + |g(x)| = h(x)».

В таких рівняннях нам в першу чергу потрібно знайти при яких значеннях змінної «х» кожен із модулів буде рівний нулеві. Для цього потрібно кожен підмодулевий вираз прирівняти до нуля та знайти розв’язки отриманого рівняння.

Перший модуль:

x² - 4x + 3 = 0

Має розв’язки:

x = 1; x = 3

Другий модуль:

x² - 5x + 6 = 0

Має розв’язки:

x = 2; x = 3

Тепер ми можемо нанести отримані розв’язки на координатну пряму:

Давайте відразу розіб’ємо наші пряму на проміжки на яких буде знаходити знак кожного модуля. Наприклад, візьмемо такі проміжки: «(-∞; 1)», «[1; 2)», «[2; 3]», «(3; + ∞)». Пам’ятаємо, що число в одному проміжку має бути включеним (квадратна дужка), а в іншому не включеним (кругла дужка).

Тепер потрібно знайти знак кожного модуля на кожному проміжку. Це можна зробити підставляючи число з кожного проміжку в підмодулевий вираз і дивитися на знак результату.

Наприклад, візьмемо проміжок «(-∞; 1)» і підставимо в кожен підмодулевий вираз число «0».

x² - 4x + 3: 0² - 4∙0 + 3 = 3

x² - 5x + 6: 0² - 5∙0 + 6 = 6

Аналогічні дії робимо з іншими проміжками й отримаємо такі знаки модулів:

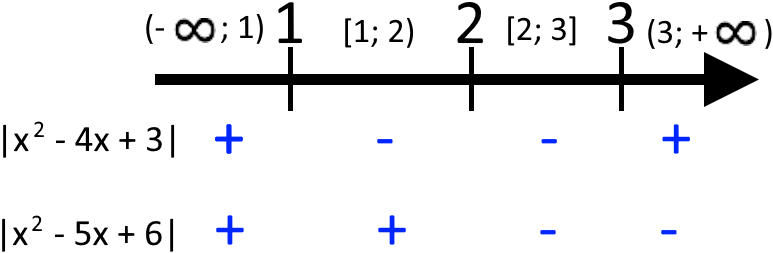
Тепер потрібно розкрити модулі на кожному проміжку та розв’язати отримане рівняння. Після чого перевіряємо чи отриманий розв’язок належить обраному проміжку.

Проміжок: «(-∞; 1)», знаки модулів: «+», «+».

Враховуючи, що обидва модулі мають знак «+», то можна ці модулі просто забрати. Матимемо:

x² - 4x + 3 + x² - 5x + 6 = 1

Розв’язуємо отримане рівняння:

2x² - 9x + 9 - 1 = 0

2x² - 9x + 8 = 0

Отримаємо такі розв’язки:

x = /9 + √17/4; x = /9 - √17/4

Зауважимо, що жоден з отриманих розв’язків не належить проміжку «(-∞; 1)», тому на даному проміжку розв’язків не має.

Проміжок: «[1; 2)», знаки модулів: «-», «+».

-(x² - 4x + 3) + x² - 5x + 6 = 1

-x² + 4x - 3 + x² - 5x + 6 = 1

-x + 3 = 1

-x = 1 - 3

-x = -2

x = 2

Даний розв’язок не належить проміжку «[1; 2)», тому на даному проміжку розв’язків не має.

Проміжок: «[2; 3]», знаки модулів: «-», «-».

-(x² - 4x + 3) - (x² - 5x + 6) = 1

-x² + 4x - 3 - x² + 5x - 6 - 1 = 0

-2x² + 9x - 10 = 0 |∙(-1)

2x² - 9x + 10 = 0

Будемо мати розв’язки:

x = /5/2 = 2,5; x = 2

Оскільки, обидва розв’язки належать проміжку, то вони будуть розв’язками початкового рівняння.

Проміжок: «(3; + ∞)», знаки модулів: «+», «+».

Оскільки, на даному проміжку ми маємо такі ж самі знаки як і на проміжку «(-∞; 1)», то ми будемо мати такі ж розв’язки:

x = /9 + √17/4; x = /9 - √17/4

В проміжок входить лише розв’язок:

x = /9 + √17/4

Відповідь: 2; 2,5; /9 + √17/4.

9) Розв’язати рівняння «||x + 1| - |x - 3|| = |x|».

Звернемо увагу, що ми маємо зовнішній модуль. І по зовнішньому модулі ми маємо рівняння вигляду «|f(x)| = |g(x)|». Тому, будемо мати два рівняння.

Перше:

|x + 1| - |x - 3| = х

Друге:

|x + 1| - |x - 3| = -х

Обидва рівняння мають тип «|f(x)| + |g(x)| = h(x)».

Ми маємо однакові модулі, тому принцип розв’язання буде в обох випадках схожим.

Знайдемо значення при яких кожен модуль рівний нулеві.

x + 1 = 0

x = -1

x - 3 = 0

x = 3

Наносимо на координатну пряму:

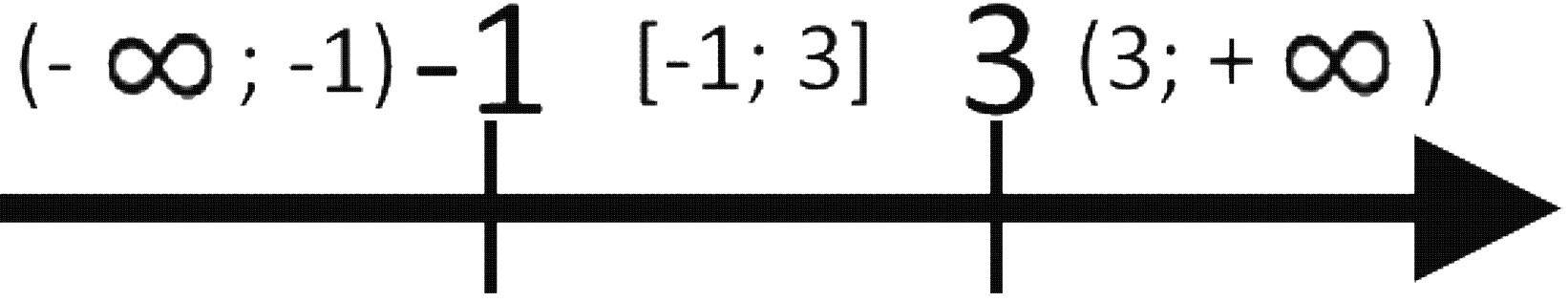
Отримаємо такі проміжки: «(-∞; -1)», «[-1; 3]», «(3; +∞)».

Знаходимо знаки кожного модуля на кожному проміжку. Матимемо:

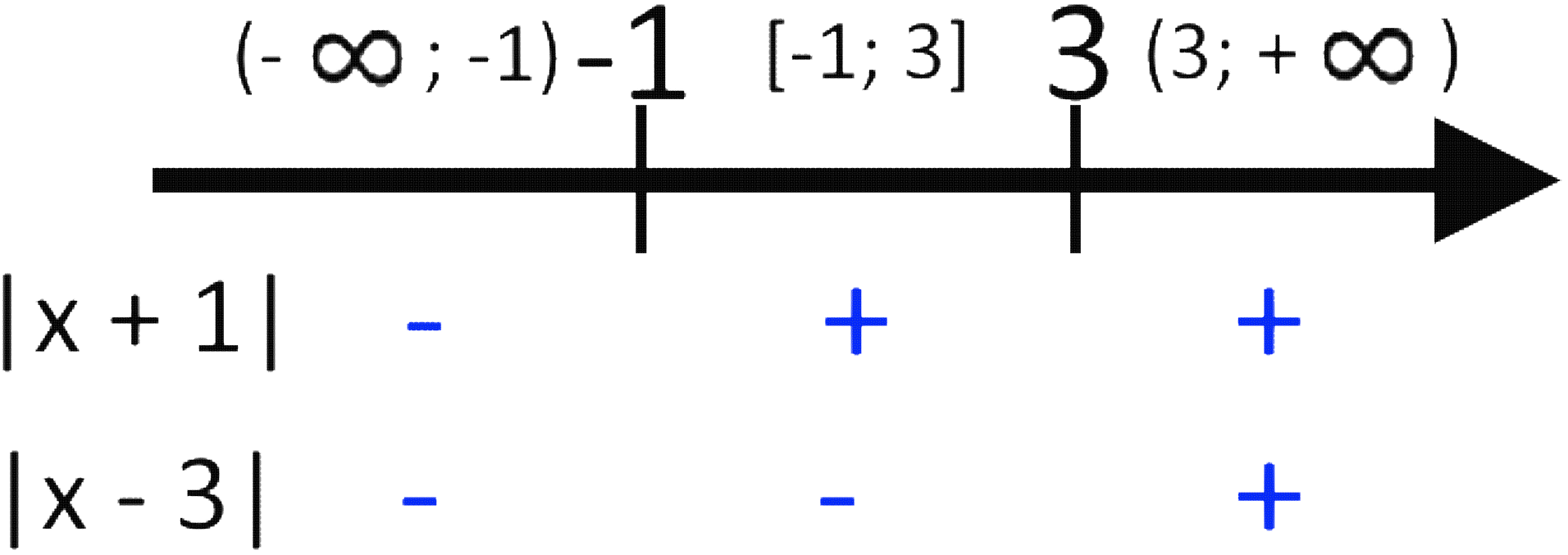
Розв’яжемо перше рівняння.

Проміжок: «(-∞; -1)», знаки модулів «-», «-».

-(x + 1) - (-(x - 3)) = x

-x - 1 + x - 3 = x

x = -4

Даний розв’язок належить проміжку, тому він нам підходить.

Проміжок: «[-1; 3]», знаки модулів «+», «-».

x + 1 - (-(x - 3)) = x

x + 1 + x - 3 = x

x = 2

Даний розв’язок належить проміжку, тому він нам підходить.

Проміжок: «(3; +∞)», знаки модулів «+», «+».

x + 1 - (+(x - 3)) = x

x + 1 - x + 3 = x

x = 4

Даний розв’язок належить проміжку, тому він нам підходить.

Розв’яжемо друге рівняння.

Проміжок: «(-∞; -1)», знаки модулів «-», «-».

-(x + 1) - (-(x - 3)) = -x

-x - 1 + x - 3 = -x

-x = -4

x = 4

Даний розв’язок не належить проміжку, тому він нам не підходить.

Проміжок: «[-1; 3]», знаки модулів «+», «-».

x + 1 - (-(x - 3)) = -x

x + 1 + x - 3 = -x

3x = 2

x = /2/3

Даний розв’язок належить проміжку, тому він нам підходить.

Проміжок: «(3; +∞)», знаки модулів «+», «+».

x + 1 - (+(x - 3)) = -x

x + 1 - x + 3 = -x

3x = 4

x = /4/3

Даний розв’язок не належить проміжку, тому він нам не підходить.

Відповідь: -4; /2/3; 2; 4.