Поняття «множин» та «підмножин» зустрічається надзвичайно часто не лише в математиці, а і у повсякденному житті. Для того щоб простіше зрозуміти, що таке множина варто дати їй означення.

Множина це сукупність однорідних (однотипних) об’єктів (речей, предметів, величин), які називають її елементами.

Відповідно, підмножина це сукупність однорідних об’єктів, які є частиною якоїсь множини.

Для прикладу, учні одного класу будуть утворювати множину. Відповідно, кожен учень є елементом цієї множини.

Ви та ваші батьки/діти будуть утворювати множину яку називають сім’єю. Відповідно, кожен член сім’ї є елементом множини.

Якщо ви читаєте даний текст, то з великою ймовірністю навчаєтеся або навчалися у школі. Під час навчання була велика кількість предметів але в один день проводилися заняття лише з деяких предметів. Відповідно, ці деякі предмети утворюватимуть підмножину. Адже, це є частина предметів з усіх можливих.

Множини позначають великими буквами латинського алфавіту: «A», «B», «C», «D», … .

Елементи множини записують у фігурних дужках розділяючи комою (можуть і крапкою з комою). Наприклад, напишемо множену «А» з елементами які є цілими числами від «-1» до «3»:

A = {-1, 0, 1, 2, 3}

Також, можемо написати множену «В» елементами якої є букви:

B = {a, b, c, d}

Якщо елемент належить множині, то це можна записати так:

Елемент ∈ Множина

Наприклад, елемент «с» належить множині «В». Тому, ми можемо це записати так: «c ∈ B».

Якщо елемент не належить множині, то це можна записати так:

Елемент ∉ Множина

Наприклад, елемент «с» не належить множині «А». Тому, ми можемо це записати так: «c ∉ A».

Перші множини які ви зустрічаєте в математиці є числовими.

Множина називається числовою, якщо її елементами є лише числа.

Розглянемо числові множини (основні):

Символ «∪» називають «об’єднанням». Він об’єднує елементи двох (або більше) множин в одну множину.

Наприклад, якщо ми маємо «A = {2, 4}» і «B = {7, 8}», то в якості об’єднання цих множин ми можемо записати множину «C» («A ⋃ B = C») з елементами «{2, 4, 7, 8}» («C = {2, 4, 7, 8}»).

Об’єднання множин можна схематично зобразити у вигляді малюнку (зафарбована частина це кінцевий результат):

Символ «∩» називають «перерізом». Він вибирає спільні елементи двох (або більше) множин в одну множину.

Наприклад, якщо ми маємо «A = {1, 2, 3, 4}» і «B = {0, 2, 4, 5}», то в якості перерізу цих множин ми можемо записати множину «C» («A ∩ B = C») з елементами «{2, 4}» («C = {2, 4}»).

Переріз множин можна схематично зобразити у вигляді малюнку (зафарбована частина це кінцевий результат):

Символ «\» називають «різницею». Він забирає елементи з лівої множини, якщо вони є у правій множині (тобто, забираються спільні елементи).

Наприклад, якщо ми маємо «A = {1, 2, 3, 4}» і «B = {0, 2, 4, 5}», то в якості різниці цих множин ми можемо записати множину «C» («A \ B = C») з елементами «{1, 3}» («C = {1, 3}»).

Переріз множин можна схематично зобразити у вигляді малюнку (зафарбована частина це кінцевий результат):

В кожній множині (підмножині) є як мінімум один елемент. Цей елемент позначають символом «∅» і називають «порожньою множиною».

Тому, якщо під час перерізу ви не матимете спільних елементів у множинах, то спільним елементом (перерізом цих множин) буде елемент «порожньої множини» («∅»).

Як ми вже вияснили підмножиною, називають множину елементи якої є частиною елементів іншої множини (спрощене формулювання).

Якщо якась множина «А» є підмножиною множини «В», то це можна записати за допомогою символу «⊂», тобто «A ⊂ B» (або «B ⊃ A»).

Наприклад, якщо множина «А» має елементи «{1, 3}» («A = {1, 3}»), а множина «В» має елементи «{1, 2, 3, 4}» («B = {1, 2, 3, 4}»), то ми можемо сказати, що множина «А» є підмножиною множини «В».

Зауважимо, що ВСІ елементи підмножини мають бути в множинні. Якщо, в множинні «А» є хоча б один елемент якого не має в множинні «В», то вона (множина «А») не може бути підмножиною множини «В».

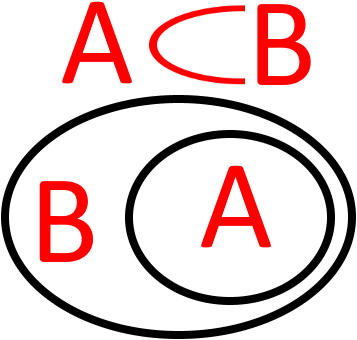
Підмножину множини можна схематично зобразити у вигляді малюнку: