Доволі часто виникає потреба намалювати не точний графік функції (тобто, не виконувати побудову по точках, тому не потрібно робити таблицю через які точки проходить даний графік), а лише ескіз даного графіка (приблизний малюнок).

В деяких випадках ми можемо використати базовий графік функції та його зміщення відносно центру координат.

Наведемо вигляди деяких базових функцій:

Пригадати графіки даних функцій ви можете тут.

Також, відразу зауважимо, що в загальному вигляді функцію можна записати так: «y = f(x)», де «f(x)» буде довільною базовою функцією (тобто, на місті «f(x)» може бути будь-яка базова функція «x», «x²», «x» і так далі).

<и>Зміщення по осі «ОУ». Вигляд функції «y = f(x) ± a»

Якщо до базового вигляду функції додати/відняти якесь число, то графік даної функції зміститься по осі «ОУ».

У випадку, коли ми додаємо число, то графік функції підніметься в гору на дане число (на дану кількість одиниць). Тобто, «+a = ↑»

У випадку, коли ми віднімаємо число, то графік функції опускається до низу на дане число (на дану кількість одиниць). Тобто, «-a = ↓».

Розглянемо це на прикладі функції «y = x²» (графік червоного кольору). Функція «x²» для нас є базовою.

Напишемо функцію, яка буде піднята на дві одиниці в гору. В такому випадку вона буде мати вигляд «y = x² + 2» (графік синього кольору). І функцію, яка буде опущена на три одиниці до низу. В такому випадку вона буде мати вигляд «y = x² - 3» (графік зеленого кольору).

Намалюємо дані графіки:

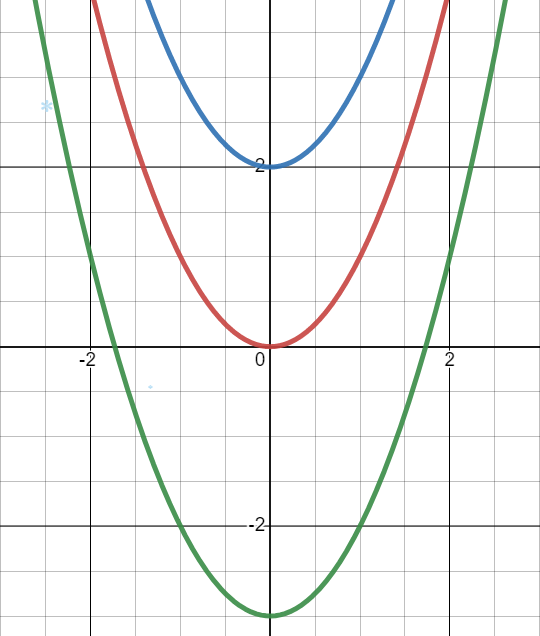
Якщо придивитися до малюнку, то можна помітити, що всі графіки є ідентичними і відрізняються лише своїм розміщенням. Кожна точка базового графіку піднялась/опустилася на одну й ту ж саму відстань (піднялась на «2» одиниці та опустилась на «3» одиниці відповідно).

Варто зауважити що ми додаємо/віднімаємо число саме до базової функції, а не до «х».

Якби ми взяли інші базові функції, то вони б виглядали так:

Зміщення по осі «ОX». Вигляд функції «y = f(x ± a)»

Якщо в базовому вигляду функції додати/відняти якесь число до аргументу функції (тобто, до «х»), то графік даної функції зміститься по осі «ОХ».

У випадку, коли ми додаємо число, то графік функції зміщується ліворуч на дане число (на дану кількість одиниць). Тобто, «+a = ←».

У випадку, коли ми віднімаємо число, то графік функції зміщується праворуч на дане число (на дану кількість одиниць). Тобто, «-a = →».

По факту ми запитуємо себе: «яким має бути «х» щоб отримати «0»?».

Розглянемо це на прикладі функції «y = x» (графік червоного кольору). Функція «x» для нас є базовою.

Напишемо функцію, яка буде зміщена на три одиниці ліворуч. В такому випадку вона буде мати вигляд «y = x + 3» (графік синього кольору). І функцію, яка буде зміщена на дві одиниці праворуч. В такому випадку вона буде мати вигляд «y = x - 2» (графік зеленого кольору).

Намалюємо дані графіки:

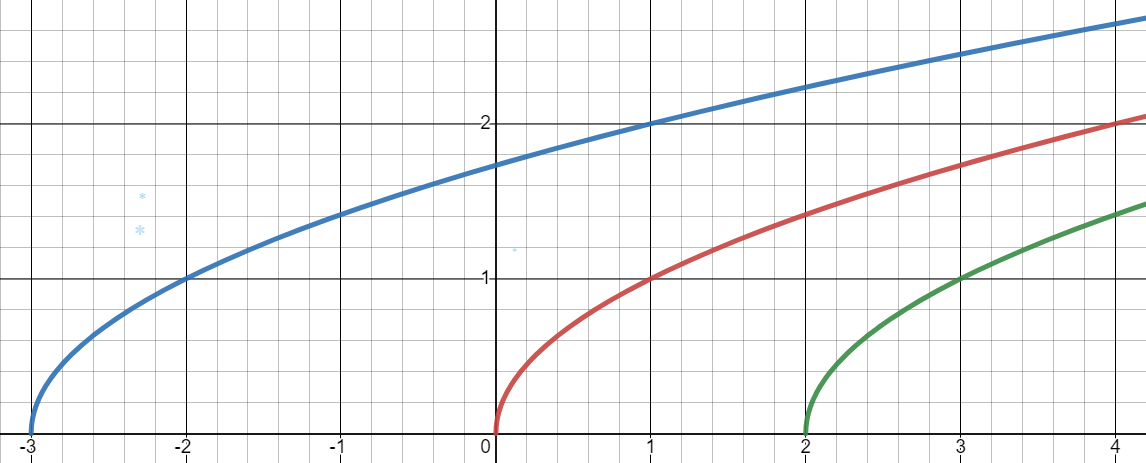
Зауважте. Графіки знову є повністю однаковими. Але зі зміщеннями в праву/ліву сторону.

Якби ми взяли інші базові функції, то вони б виглядали так:

Звуження/розширення графіку функції відносно осі «ОУ». Вигляд функції «y = a ∙ f(x)»

Якщо ми візьмемо базову функцію і помножимо її на якесь число, то в залежності від даного числа графік функції може розширитися (відштовхнутися) відносно осі «ОУ», або навпаки звузитися (прижатися) відносно осі «ОУ».

Якщо ми базову функцію будемо множити на число, яке є більшим за «1» («a > 1»), то графік нашої функції звузиться (притисниться) відносно осі «ОУ».

Якщо ми базову функцію будемо множити на число, яке є більшим за «0» і меншим за «1» («0 < a < 1»), то графік нашої функції розшириться (відштовхнеться) відносно осі «ОУ».

Зауважте! Ми не беремо від’ємні числа. Це все через те, що від’ємні числа (а саме знак «-») по іншому впливають на графік функції. Дану ситуацію розглянемо пізніше.

Візьмемо базову функцію «y = x²» (графік червоного кольору). Припустимо ми хочемо прижати її до осі «ОУ». Для цього нам необхідно помножити цю функцію на число більше за «1». Для прикладу на «2». Тоді, отримаємо: «y = 2x²» (графік синього кольору). А, якщо нам необхідно її віддалити від осі «ОУ», то потрібно помножити на число більше за «0» але менше за «1». Для прикладу на «/1/2». Тоді, отримаємо: «y = /1/2 x²» (графік зеленого кольору).

Давайте розберемось, чому це так працює. Пояснення є доволі простим. Якщо для кожної з даних функцій ми візьмемо одне й теж саме значення аргументу (тобто «х»), то ми отримаємо різні значення функції (тобто «у»).

При «х = 1», будемо мати:

Побудуємо графіки даних функцій. Для кращої демонстрації звуження/розширення функцій поставимо наші числа (по осі «ОХ»: «1», по осі «ОУ»: «/1/2», «1», «2»).

Зверніть увагу, коли графік функції прижимається до осі «ОУ», то він віддаляється від осі «ОХ» і навпаки, коли ми віддаляємося від осі «ОУ», то прижимаємося до осі «ОХ».

Звуження/розширення графіку функції відносно осі «ОХ». Вигляд функції «y = f(a ∙ x)»

Якщо ми візьмемо базову функцію і помножимо її аргумент на якесь число, то в залежності від даного числа графік функції може розширитися (відштовхнутися) відносно осі «ОХ», або навпаки звузитися (прижатися) відносно осі «ОХ».

Якщо ми аргумент базової функції будемо множити на число, яке є більшим за «1» («a > 1»), то графік нашої функції розшириться (відштовхнеться) відносно осі «ОХ».

Якщо ми аргумент базової функції будемо множити на число, яке є більшим за «0» і меншим за «1» («0 < a < 1»), то графік нашої функції звузиться (притисниться) відносно осі «ОХ».

Зауважте! Ми не беремо від’ємні числа. Це все через те, що від’ємні числа (а саме знак «-») по іншому впливають на графік функції. Дану ситуацію розглянемо пізніше.

Візьмемо базову функцію «y = x» (графік червоного кольору). Припустимо ми хочемо віддалити її від осі «ОХ». Для цього нам необхідно помножити аргумент цієї функції на число більше за «1». Для прикладу на «2». Тоді, отримаємо: «y = 2x» (графік синього кольору). А, якщо нам необхідно її притиснути до осі «ОХ», то потрібно помножити на число більше за «0» але менше за «1». Для прикладу на «/1/2» (графік зеленого кольору). Тоді, отримаємо: «y = /1/2x».

Давайте розберемось, чому це так працює. Пояснення є доволі простим. Якщо для кожної з даних функцій ми візьмемо одне й теж саме значення функції (тобто «у»), то ми отримаємо різні значення аргументу функції (тобто «х»).

При «у = 1», будемо мати:

Побудуємо графіки даних функцій. Для кращої демонстрації звуження/розширення функцій поставимо наші числа (по осі «ОХ»: «/1/2», «1», «2», по осі «ОУ»: «1»).

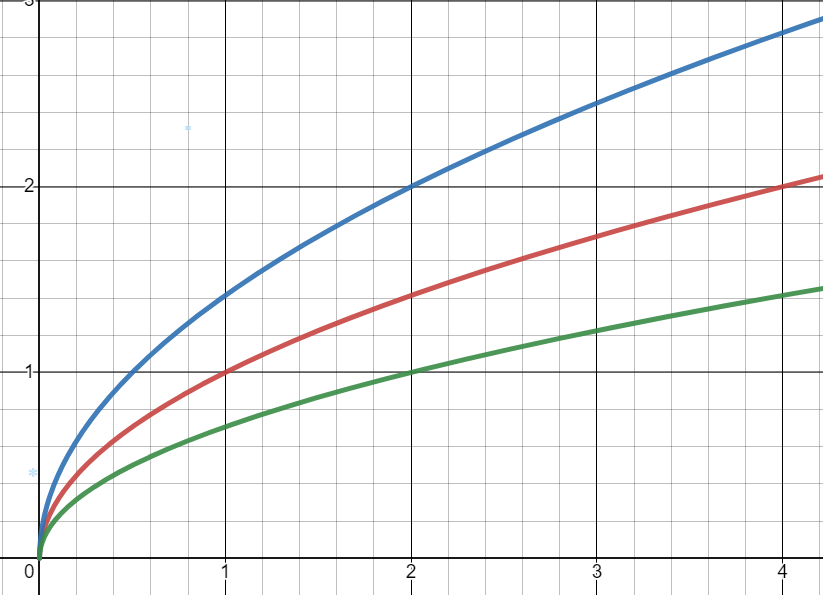
Зверніть увагу, коли графік функції прижимається до осі «ОХ», то він віддаляється від осі «ОУ» і навпаки, коли ми віддаляємося від осі «ОХ», то прижимаємося до осі «ОУ».

Дзеркальне відображення функції відносно осі «ОХ». Вигляд функції «y = -f(x)»

Якщо ми візьмемо функцію і перед нею напишемо знак «-» (по факту помножимо нашу функцію на «-1»), то її графік дзеркально (симетрично) відіб’ється (перевернеться) відносно осі «ОХ».

Тобто, це можна уявити як малюнок зроблений на одній сторінці зошита. Коли, ви закриєте цей зошит, то зроблений малюнок переб’ється на іншу сторінку симетрично (віддзеркалено) середини зошита (згину). В нашому випадку серединою зошита буде вісь «х».

Важливо розуміти, що цей мінус має відноситися до всієї функції, а не до якось єдиного числа. Для прикладу, якщо ми маємо функцію «y = x² - 4x + 5» і хочемо її віддзеркалити відносно осі «ОХ», то потрібно було помножити дану функцію на «-1». В такому випадку наша віддзеркалена функція мала б такий запис «y = -(x² - 4x + 5)». Як бачите «-» відноситься до всієї функції. Якщо розкрити дужки, то ми отримаємо «y = -x² + 4y - 5».

Візьмемо функцію «y = x - 2 + 1» (графік червоного кольору) віддзеркалимо її відносно осі «ОХ». Для цього помножимо дану функцію на «-1» (поставимо перед всією функцією знак «-»). Будемо мати «y = -(x - 2 + 1)» (або « y= -x - 2 - 1») (графік синього кольору).

Тепер для демонстрації намалюємо наші графіки:

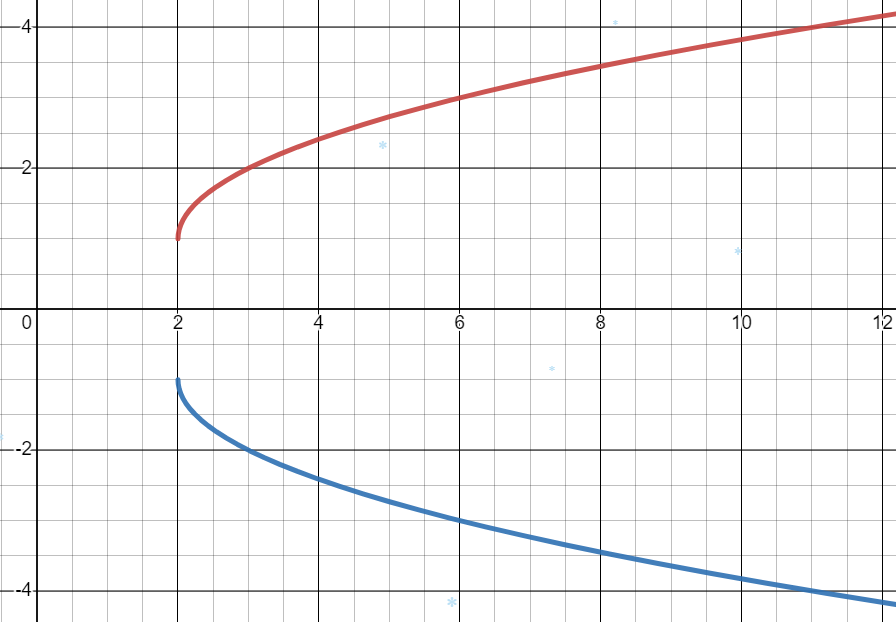
Спробуємо розібратися, чому так виходить. В загальному функцію можна записати у вигляді «y = f(x)». Коли, ми підставляємо значення замість аргументу, то вираз «f(x)» набуває якогось значення і ми отримуємо «у = а», де «а» - число. А, коли ми беремо «у = -f(x)» але те ж саме значення аргументу, то отримаємо «у = -а».

Розглянемо на нашій функції «y = x - 2 + 1». Обчислимо її значення при «х = 6». Матимемо: «y = 6 - 2 + 1 = 3». Тепер розглянемо «y = -(x - 2 + 1)» при тому ж значенні аргумента «х = 6». Матимемо: «y = -(6 - 2 + 1) = -3».

Ви можете підставити інші числа і переконатися, що отримаємо однакові результати але з протилежними знаками. Наприклад, при «х = 2» матимемо «1» та «-1»; при «х = 3» матимемо «2» та «-2».

Дзеркальне відображення функції відносно осі «ОУ». Вигляд функції «y = f(-x)»

Якщо ми хочемо віддзеркалити (симетрично відобразити) графік відносно осі «ОУ», то нам необхідно аргумент функції («х») поставити зі знаком «-» (помножити на «-1»).

Візьмемо функцію «y = x - 2 + 1» та спробуємо її графік віддзеркалити відносно осі «ОУ». Для цього аргумент функції («х») напишемо зі знаком «-». Будемо мати: «y = √(-x-2) + 1».

Побудуємо наші графіки:

В таких випадках при одних і тих же значеннях «у» ми будемо мати однакові значення «х», але з протилежними знаками.

Наприклад, коли ми візьмемо замість «у» число «2» і підставимо у наші функції, то з «y = x - 2 + 1» ми отримаємо, що «х = 6», а з «y = -x - 2 + 1» матимемо «х = -6».

Модуль функції. Відбиття графіка відносно осі «ОХ». Вигляд функції «y = |f(x)|»

Ми знаємо, що модуль «з’їдає» знак і будь-яке число по модулі буде давати додатний результат («|5| = 5», «|- 5| = 5»). Коли графік функції знаходиться під віссю «ОХ», то значення функції є від’ємним. Відповідно, коли ми візьмемо всю функцію по модулю, то ці від’ємні значення стануть додатними. При цьому графік перейде з нижньої частини у верхню. Ситуація буде дуже схожою до того моменту, коли ми ставили знак «-» перед функцією. Але, в даному випадку не вся функція віддзеркалюється, а лише та, що знаходиться під віссю «ОХ».

Розглянемо це на прикладі функції «y = x² + 4x + 2». Намалюємо цю функцію червоним кольором. І візьмемо ще функцію «y = |x² + 4x + 2|» та зробимо її графік синього кольору.

Як бачите частини графіків функції співпадають, а червона частина яка є під «ОХ» відобразилась у синю частину над «ОХ».

Модуль аргумента функції. Відбиття графіка відносно осі «ОУ». Вигляд функції «y = f(|x|)»

Коли ми беремо аргумент функції по модулю, то всі значення аргумента стають додатними і графік функції який є в лівій частини відносно осі «ОУ» починає повторювати графік з правої частини відносно осі «ОУ». Виходить, що графік з правої частини відносно осі «ОУ» додатково повторюється в лівій частині відносно осі «ОУ».

Розглянемо дану ситуацію на прикладі функції «y = x² - 4x + 3». Намалюємо її графік червоним кольором. І Візьмемо функцію «y = |x|² - 4 ∙ |x| + 3» яку намалюємо синім кольором.

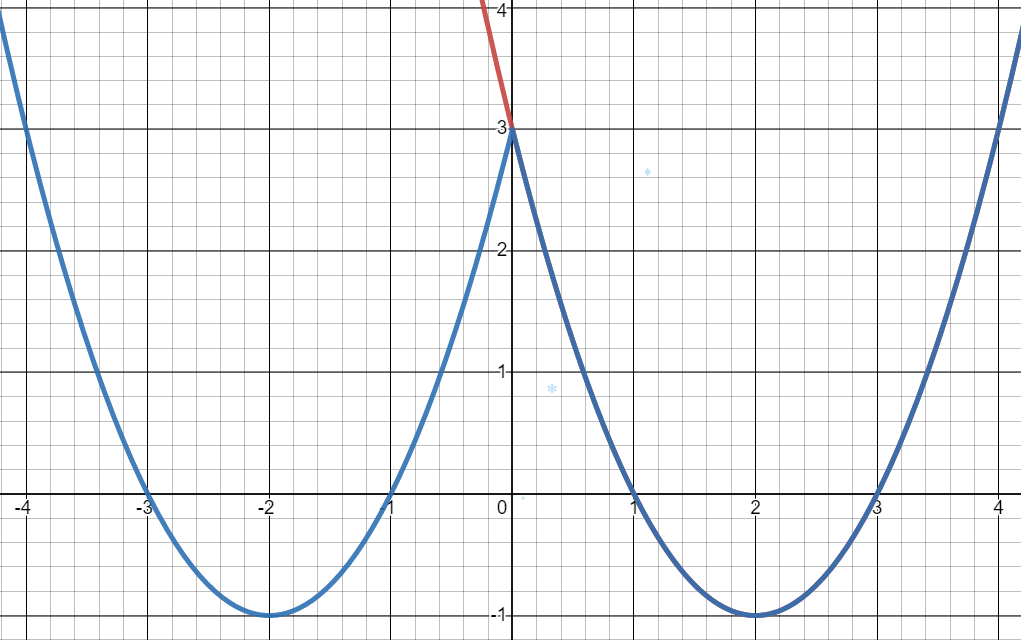
Зверніть увагу, що графік синього кольору виглядає однаково ліворуч і праворуч відносно осі «ОУ».