Числа з комою (десяткові дроби). Основні алгебраїчні дії з десятковими дробами
Відразу повідомимо, що основні алгебраїчні дії розглянуто тут. Тому варто з першу прочитати попередній матеріал.
Називаємо числа правильно
Мабуть перше, що стає не зрозумілим з перших хвилин роботи з числами із комою це як їх називати. Розглянемо їх стандартний вигляд «х, у», де «х» - ціла частина (завжди знаходиться ліворуч від коми), «у» - дробова частина (завжди знаходиться праворуч від коми). Наприклад: «6,31», «-75,8», «0,001».
Отже, для того, щоб навчитися їх правильно називати варто слідувати простим правилам (пояснення приведені для простоти):
1) Цілу частину говоримо як число добавляючи в кінці слово «цілих»: «шість цілих», «сімдесят п’ять цілих», «нуль цілих».
2) Щоб правильно назвати дробову частину вважаємо «кому» як «одиницю». Після чого необхідно порахувати скільки чисел знаходиться після коми і добавити стільки ж нулів до нашої «одиниці». Після чого називаємо число яке знаходиться після коми та додаємо в кінці число яке у нас вийшло (одиниця + нулі) так щоб воно відповідало на запитання «яких?», «яка?»: «десятих», «десята»; «сотих», «сота»; «тисячних», «тисячна» і так далі. Наприклад: у числі «6,31» є два числа після «коми», тому додаємо до одиниці два «нулі» і отримаємо «шість цілих тридцять одна сота»; «-75,8» буде «мінус сімдесят п’ять цілих вісім десятих»; «0,001» буде «нуль цілих одна тисячна».
Додавання та віднімання чисел з комою
Додавання та віднімання чисел з комою відбувається по розрядах. Не лякайтеся все дуже просто. Додавання або віднімання по розрядах означає, що до цілої частини додається/віднімається ціла частина (цілі частини додаються відповідно як цілі числа), до десятих – десяті, сотих – соті і так далі.
! Додавання як і віднімання необхідно починати з правого краю.
Наприклад: «14,5 + 3,76».
Отже: Соті частини додаємо між собою. Оскільки в числі «14,5» не має сотої частини, то вона вважається «0». Отримаємо: «0 + 6 = 6»;
Десяті «5 + 7 = 12». Оскільки число вийшло більшим за «9», то воно перейшло у новий розряд (на один більше). Тобто: «2» - залишається десятком, а «1» вже стає цілою частиною (якщо, така ситуація вийшла б при додаванні сотих, то «2» - буде сотою, а «1» - десятою частиною). У випадку коли б вийшло число «23», «57» і подібні, то до лівого числа додавалося б «2» або «5»;
Цілі «14 + 3 = 17» і варто пам’ятати, що при додаванні десятих у нас з’явилася «1» яка додається до цілої частини. Тобто, отримаємо: «17 + 1 = 18».
Результат: «18,26»
«3,76 – 14,5»
Виконую віднімання необхідно в першу чергу визначити знак результату. Для цього потрібно поставити знак більшого числа. Пам’ятаємо, що знак числа знаходиться перед числом! Якщо перед числом не має ні я кого знаку, то це означає, що число є додатним.
Отже «3,76» є додатне (оскільки перед ним не має жодного знаку), «14,5» є від’ємне (оскільки перед ним стоїть знак мінус). «14,5» є більшим за «3,76» це означає, що результат буде від’ємним.
Після того як визначили знак результату, необхідно, знайти різницю. Для цього віднімаємо від більшого числа менше. Дотримуючись тих же правил, що і при додаванні. Тобто, віднімаємо по розрядах починаючи з правої сторони!
«3,76 – 14,5 = - (14,5 – 3,76)» - знак результату «-»
«14,5 – 3,76» - віднімання від більшого числа менше
Отже. Соті: знову ж таки в «14,5» сотих не має тому вважаємо, що вони «0». Від «0» необхідно відняти «6». «0» є меншим за «6», то це означає, що необхідно позичити «1» в числа, що стоїть ліворуч, тобто у «5». Після чого отримаємо «10» (одиниця позичена в лівого числа є по факту «10» яку ми додаємо до числа для якого позичали цю одиницю, а оскільки у нас був «0» то будемо мати «10 + 0 = 10»). Тому отримаємо:
«10 – 6 = 4» - сота частина
Десяті: Відразу зауважимо, що від «5» ми забрали «1», тому вже маємо:
«5 – 1 = 4»
Тепер необхідно від «4» відняти «7». «4» є меншим за «7», тому необхідно позичити «1» в лівого числа. Після чого отримаємо:
«10 + 4 = 14»
І вже від «14» необхідно відняти «7»
«14 – 7 = 7» - десята частина
Рекомендація. Якщо ви позичаєте «1», то краще від «10» відняти число після чого до результату додати число для якого позичали «1». Тобто:
«10 – 7 = 3»
«3 + 4 = 7»
Цілі: Оскільки ми позичили «1» у «14», то тепер маємо:
«14 – 1 = 13»
І отримаємо після віднімання цілих:
«13 – 3 = 10» - ціла частина
Отже кінцевий результат віднімання «14,5 – 3,76», буде «10,74».
! Ми з самого початку визначили, що результатом віднімання буде від’ємне число. Тому потрібно відповідь записати зі знаком «-»:
«3,76 – 14,5 = - 10,74»
Дуже часто виникають моменти коли складно зрозуміти яка дія зараз виконується.
Наприклад: «- 5,7 + 7,9»; «- 5,7 - 7,9».
! Якщо в чисел є однакові знаки «5,7 + 7,9» чи «- 5,7 - 7,9», то необхідно числа додати та поставити їх спільний знак. Якщо у чисел знаки різні «- 5,7 + 7,9» чи «5,7 - 7,9», то числа віднімаються по принципу, що описаний вище.
Доволі зручно виконувати дії додавання/віднімання чисел з комою у стовпчик. Для цього необхідно виконати таку послідовність дій.
Увага! Якщо дія віднімання, то відразу знаходимо знак результату та визначити яке число від якого віднімаємо (від більшого менше).
Для прикладу візьмемо вже числа з якими виконували дії, що б можна було порівняти.
Дії:
1. Записуємо перше число (одна клітинка = один знак):
| 1 | 4 | , | 5 |
2. Ставимо кому під комою:
| 1 | 4 | , | 5 |
| , |
3. Переписуємо друге число відносно нижньої коми(одна клітинка = один знак):
| 1 | 4 | , | 5 | |
| 3 | , | 7 | 6 |
4.Ставимо знак дії (додавання або віднімання). Щоб не писати двічі одне і теж ми поєднаємо знаки «+» та «-» в один «±». Знак ставиться з краю ліворуч між двома числами:
| ± | 1 | 4 | , | 5 | |
| 3 | , | 7 | 6 |
5. Записуючи результат необхідно дотримуватися головного правила: «кома має знаходитися під комою». Також на місці порожніх клітинок ви можете записувати «0» для вашої зручності. Дії додавання та віднімання виконуються стовпцями (для демонстрації виділимо їх різними кольорами). Тобто до числа, що знаходиться з верху додається або віднімається нижнє. Для прикладу додаймо та віднімемо наші числа (не забуваємо про числа які додаються при результаті більшому за «9» та «1» яку можна позичати):
| + | 1 | 4 | , | 5 | 0 |
| 0 | 3 | , | 7 | 6 | |
| 1 | 8 | , | 2 | 6 | |
| - | 1 | 4 | , | 5 | 0 |
| 0 | 3 | , | 7 | 6 | |
| 1 | 0 | , | 7 | 4 | |
Результат: «14, 5 + 3,76 = 18,26», «3,76 – 14,5 = - (14,5 – 3,76) = - 10,74»
Множення та ділення чисел з комою на числа в яких є нулі:
Часто доводиться множити або ділити числа з комою на числа в яких є нулі (в кінці числа). Наприклад: «1,22 · 30», «3,2 · 100», «56,3 : 1000», «44,6 : 20», «2,2 · 110», «51 : 10» та багато інших.
В такому випадку можна трішки спростити собі життя.
Якщо число з комою множиться на число з нулями, то кому можна зміщувати праворуч на стільки ж цифр скільки нулів (один нуль – зміщення на одну цифру праворуч). Після чого необхідно буде помножити числа які залишилися (на справді можна множити числа, а потім зміщувати кому. Це вже на ваш розсуд).
Наприклад:
«1,22 · 30 = 12,2 · 3 = 36,6»
«1,4 · 100 = 140»
При діленні відбувається з точністю до навпаки. Необхідно зміщувати кому ліворуч на стільки ж цифр скільки нулів. Цей спосіб корисний коли число ділиться на «10», «100», «1000» і так далі. При ділені наприклад на «370» він вже є не зовсім зручним. В такому випадку краще ділити як описано нижче.
Наприклад:
«36 : 10 = 3,6»
«786 : 10000 = 0,0786»
Множення чисел з комою:
Множити числа з комою доволі просто. Для цього необхідно порахувати скільки цифр є після коми в числах які множаться. Потім помножити ці числа забравши кому (просто уявляємо, що її не має). Отримавши результат необхідно стати в правий край і рухатися на таку ж саму кількість цифр ліворуч скільки ми порахували з самого початку (скільки цифр після коми до множення стільки ж саме має бути після множення).
Наприклад: «2,36 · 5,4»
В даних числах є три цифри після коми («36» та «4»).
Тепер необхідно помножити «236» на «54»:
«236 · 54 = 12744»
Тепер стаємо в правий кінець числа і рухаємося ліворуч на стільки ж цифр скільки було до множення (в нашому випадку три):
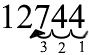
Отримаємо:
«12,744»
Отже:
«2,36 · 5,4 = 12,744»
Пам'ятаємо! Скільки цифр було після коми до множення стільки ж має бути після множення.
Ділення чисел з комою:
Коли необхідно поділити числа серед яких хоча б одне є з комою, то є два (можливо більше, але ці способи рекомендую вам я) простих способи:
1. Необхідно порахувати яка максимальна кількість цифр є після коми. Після чого помножити числа які діляться на «1 + стільки ж нулів скільки є максимально цифр після коми».
Наприклад: «3,56 : 0,2» - максимальна кількість цифр після коми «2» (у «3,56»), тому необхідно «3,56» та «0,2» помножити на «100» (1 + два нулі, бо максимальна кількість цифр є дві).
Отримаємо: «(3,56 · 100) : (0,2 · 100) = 356 : 20»
2. Необхідно в обох числах одночасно зміщувати кому праворуч поки вона не опиниться з правого краю. Важливо! Якщо в одному з чисел кома опинилася у правому кінці, а в іншому ні, то необхідно все одно зміщувати її праворуч. На місці «порожніх» зміщень необхідно поставити нулі. Така ж ситуація виникне, якщо одне число буде з комою, а інше ні.
Ось так це виглядає:
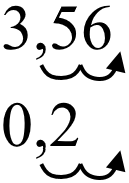
Отримаємо: «356 : 20»
Після чого залишається лише розділити данні числа. Детальніше можна прочитати тут.
Ділення чисел до десяткових дробів:
Часто доводиться ділити числа до десяткових дробів. На справді таке ділення не сильно відрізняється від ділення з остачею. Але звісно не позбавлене своїх нюансів. Розглянемо відразу на прикладі:
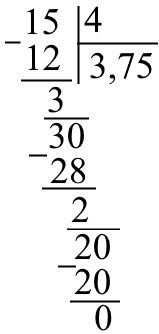
Погляньте. Після того як поділили «15» на «4» остача вийшла «3». Після чого до «3» був дописаний «0» якого не має. Тому в результаті ділення необхідно поставити кому. Важливо! Якщо перед комою не буде ні якого числа то необхідно поставити нуль. Після чого отримаємо ділення «30» на «4». Результат буде «7», остача «2». Знову ж таки до «2» дописуємо нуль, але кома більше одного разу не ставиться! Після чого продовжуємо ці дії поки остача не вийде нуль або поки не отримаємо необхідну точність числа (тобто певну кількість знаків після коми).
Варто зауважити, що у випадку коли дописуємо декілька нулів підряд, то в результат необхідно написати на один нуль менше.
Наприклад:
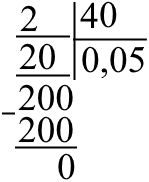
Перший нуль в результаті (той, що ліворуч від коми) з’явився через те, що перед комою не було ні якого числа. Нуль, що стоїть після коми з’явився через те, що до «2» дописали два нулі підряд (пам’ятаємо, що в результат записуємо на один нуль менше чим до діленого числа). Таке може відбуватися на будь якому етапі прикладу:

Перетворення десяткових дробів на звичайні та навпаки:
Розпочнемо із перетворення звичайних дробів у десяткові. В такому випадку необхідно просто розділити чисельник на знаменник способом ділення чисел з комою (вище описано). Не має значення чи до цього дріб був правильним чи неправильним. У випадку якщо дріб правильний та є ціла частина, то необхідно в кінці просто додати цілу частину до числа, що вийде після ділення.
Наприклад: Перетворити у десятковий дріб число: «3/1/2».
Розділимо «1» на «2» способом описаним раніше. Отримаємо число «0,5». Після цього необхідно просто додати «3» та «0,5» і отримаємо: «3,5».
Перетворити у десятковий дріб число: «/5/2».
Розділивши «5» на «2» отримаємо: «2,5». Оскільки не має виділеної цілої частини, то не потрібно нічого додавати.
Перетворювати з десяткових дробів у звичайні ще простіше. Якщо є ціла частина, то можна діяти за двома принципами. Перетворювати у правильний або неправильний дріб. Для перетворення у неправильний дріб необхідно порахувати скільки чисел є після коми. Після чого все число без коми написати в чисельнику, а знаменник записуємо так: «1 + стільки ж нулів скільки чисел є після коми».
Наприклад: «2,354» має «3» числа після коми. Отже, у знаменнику буде «1 + три нулі».
Отримаємо: /2354/1000
Для перетворення у правильний дріб або у випадках коли ціла частина є нульовою необхідно в чисельник записувати лише числа, що стоять після коми, а цілу частину писати як у звичайному дробі. Знаменник визначаємо за тим же принципом.
Візьмемо за приклад знову ж таки число «2,354».
Отримаємо: 2/354/1000