Нерівності
Якщо «a» і «b» деякі числа або вирази (можуть бути дробові, цілі, від’ємні, додатні числа або якісь вирази), то їх можна порівняти. Є п’ять варіантів порівняння: (ще кажуть «не менше», далі «більше-рівне»), (ще кажуть «не більше», далі «менше-рівне»), Їх запам’ятати доволі просто. Необхідно подивитися на лівий край. Якщо він великий, то це знак більше або більше-рівне Якщо він маленький то менше або менше-рівне Відповідно залишився знак рівності
Знаки та називають знаками строгих нерівностей. Знаки та називають знаками нестрогих нерівностей.
Розглянемо як порівнюються числа (вирази розглядатимемо пізніше).
Зауважимо, що будь яке додатне число або нуль є більшим за будь яке від’ємне число:
0,0001 > -10000
Можна запам’ятати так. Якщо уявити числову пряму, то чим правіше число знаходиться (чим ближче до «х») тим воно і більше.
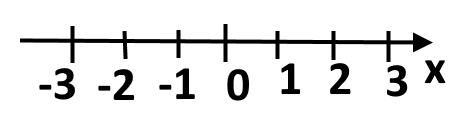
Порівняння цілих чисел та раціональних чисел
З цілими або раціональними числами зазвичай не виникає труднощів. Хоча є декілька доволі простих способів порівнювати ці числа.
В першу чергу порівнюють по знаках. Якщо числа різних знаків, то більше те число яке є додатнім. Якщо числа додатні, то можна відняти від першого числа друге, після чого оцінити їх різницю. Якщо різниця від’ємна, то друге число більше за перше. Якщо додатна, то перше число більше. Якщо різниця рівна нулю, то числа рівні.
Також часто порівнюють від’ємні числа (цілі або дробові вирази) (якщо обидва числа є від’ємними, якщо одне від’ємне інше ні так робити не можна!) за допомогою модуля. Тобто беруть модуль обох чисел (числа з від’ємних стають додатними). Після чого порівнюють числа (якщо ви вже орієнтуєтеся в цьому. Або ж можна взяти модуль чисел та відняти їх як у попередньому випадку, але знак буде протилежний. Тобто, якщо при відніманні число вийде від’ємним, то друге (праве) число є меншим), а між початковими ставлять протилежний знак.
– різниця при порівнянні додатних чисел від’ємна, то:
– різниця при порівнянні від’ємних чисел від’ємна, то
Аналогічно порівнюються раціональні числа.
Порівняння дробів
Якщо у дробів однакові знаменники і якщо обидва дроби є додатними, то більший той дріб в якого чисельник більший, а якщо обидва дроби є від’ємними то більший той у якого знаменник менший.
/2/5 < /3/5; -/42/51 > -/48/51 (не забувайте як порівнюються від’ємні числа)
Якщо у дробів однакові чисельники і якщо обидва дроби є додатними, то більший той дріб в якого знаменник менший, а якщо обидва дроби є від’ємними, то більший той у якого знаменник більший.
/7/3 > /7/4; -/9/2 < -/9/5 (не забувайте як порівнюються від’ємні числа)
Якщо у дробів чисельники та знаменники різними, а дроби є одного знаку, то їх зводять до спільного чисельника або знаменника після чого порівнюють за попередніми варіантами. Або переводять у десяткові дроби (такого вигляду: після чого порівнюють.
Якщо у дробів є ціла частина, то в першу чергу порівнюють по ній (як звичайні цілі числа) і лише коли цілі частини рівні, то порівнюють між собою дробові частини.
Властивості числових нерівностей
1. Якщо то якщо то
2. Якщо та то (властивість транзитивності)
3. Якщо то
4. Якщо та - додатне число то
Ця властивість має такий зміст: якщо обидві частини правильної нерівності помножити на одне й те ж саме додатне число, то отримаємо правильну нерівність.
5. Якщо і - від’ємне число то
Ця властивість має такий зміст: якщо обидві частини правильної нерівності помножити на одне й те саме від’ємне число і змінити знак початкової нерівності на протилежний, то отримаємо правильну нерівність.
6. Якщо і то Якщо почленно додати дві правильні нерівності одного знака, то отримаємо правильну нерівність.
7. Якщо - додатні числа, до того ж і то Якщо почленно перемножити правильні нерівності одного знака, ліві і праві частини яких додатні числа, то отримаємо правильну нерівність.
8. Якщо і то
9. Якщо то
10. Якщо то для будь-якого натурального числа «n» виконується нерівність
Числові проміжки
| Вид проміжку | Геометричне зображення | Позначення | Запис за допомогою нерівностей |
| Інтервал |  | (a ; b) | a < x < b |
| Відрізок | 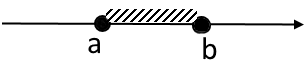 | [a ; b] | a ≤ x ≤ b |
| Півінтервал |  | (a ; b] | a < x ≤ b |
| Півінтервал |  | [a ; b) | a ≤ x < b |
| Промінь |  | [a ; +∞) | x ≥ a |
| Промінь |  | (-∞ ; b] | x ≤ b |
| Відкритий промінь |  | (a ; +∞) | x > a |
| Відкритий промінь |  | (-∞ ; b) | x < b |
На практиці не завжди використовують терміни «інтервал», «відрізок», «півінтервал», «промінь», а замінюють їх спільною назвою «числовий проміжок».
Переріз числових проміжків або множин (двох або більше) – це проміжок, який складається з тих чисел, які належать одночасно всім проміжкам. Тобто, це спільна частина проміжків.
Уявіть ситуацію. У вас та у вашого(-ї) друга/подруги є по одному бутербродові. У вас бутерброд складається з хліба та ковбаси, а у друга/подруги хліба та сиру. Оскільки переріз це спільна річ з двох (або більше) числових проміжків або множин, то вашим перерізом буде хліб, оскільки він є в обох бутербродах.
Переріз позначають символом «∩»
Об’єднання числових проміжків або множин (двох або більше) – це проміжок, який складається з тих чисел, які належать хоча б одному з даних проміжків.
Візьмемо попередній приклад із бутербродами. Об’єднання збирає до кучі все, що є, але лише по одному разу. Тобто об’єднання буде таким: один хліб, ковбаса та сир.
Об’єднання позначають символом «∪»
Переріз проміжків (множин) – це завжди проміжок (множина). Об’єднання проміжків (множин) не завжди є проміжком (множиною), це зумовлено тим, що може не виявитися спільних елементів або буде лише один елемент.
Лінійні нерівності
Лінійною називається нерівність виду де
Розв’язками нерівності з однією змінною називається множина таких значень змінної, яка перетворює її на правильну числову нерівність.
При розв’язуванні нерівностей використовуються такі властивості:
1. Якщо з однієї частини нерівності перенести в іншу доданок з протилежним знаком, то утвориться нерівність, рівносильна даній.
2x + 4 > x + 7
2x - x > 7 - 4
x > 3
2. Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то утвориться нерівність, рівносильна даній.
2x ≤ 6
2x ≤ 6 | ∶ 2
x ≤ 3
3. Якщо обидві частини нерівності помножити або поділити на одне й те саме від’ємне число, змінивши при цьому знак нерівності на протилежний, то утвориться нерівність, рівносильна даній. Тобто при множенні або ділені на від’ємне число, знак нерівності змінюється на протилежний.
-3x > 9
-3x > 9 | : (-3)
x < -3
Це основні моменти на які необхідно звертати увагу при розв’язувані лінійних нерівностей з однією змінною. У всьому іншому вони розв’язуються так само як лінійні рівняння з однією змінною.
У випадках, коли зникає, а нерівність є правильною маємо: - тобто, є будь яке число.
У випадках, коли зникає, а нерівність є не правильною маємо: - тобто, розв’язків не має.
Подвійна нерівність
Нерівність вигляду:
a < x < b
Де називають, подвійною, оскільки в ній є два знаки нерівності. Ці знаки мають бути направленими в одну сторону.
Якщо така нерівність є лінійною. Тобто «х» є без степеня, кореня, модуля, не у знаменнику і так далі, то її розв’язувати доволі просто.
1. Необхідно, для своєї зручності, закрити ліву або праву частину нерівності.
2. Виконати дії для розв’язання нерівності, що залишилася.
3. Виконати аналогічні дії з тією ж частиною яку закрили.
Наприклад:
2 < /7 - 2x/3 ≤ 5
Для своєї зручності забираємо ліву частину і після цього отримаємо звичайну нерівність. Після чого робимо дію з тим, що залишилося.
– забрали ліву частину
Щоб розв’язати таку нерівність необхідно помножити обидві частини нерівності на Оскільки є додатнім числом, то знак нерівності не змінюється.
Оскільки ми помножили «праву» частину нерівності помножили на то аналогічно маємо поступити і з «лівою» частиною.
6 < 7 - 2x ≤ 15
Знову забираємо ліву частину.
7 - 2x ≤ 15
Тепер необхідно перенести у протилежну сторону змінивши при цьому знак на протилежний.
-2x ≤ 15 - 7
Оскільки в правій частині у нас з’явилося то і в лівій частині воно також має з’явитися.
6 - 7 < -2x ≤ 15 - 7
-1 < -2x ≤ 8
Забираємо ліву частину.
-2x ≤ 8
Тут необхідно поділити на Оскільки число є від’ємним, то знак нерівності зміниться на протилежний.
x ≥ 8 ∶ (-2)
Аналогічні дії робимо з лівою частиною.
-1 ∶ (-2) > x ≥ 8 ∶ (-2)
/1/2 > x ≥ -4
Вже знайшли «х» але прийнято записувати відповідь починаючи з меншого числа. Тому необхідно розвернути нашу нерівність.
-4 ≤ x < /1/2
Подвійну нерівність також можна переписати за допомогою системи рівнянь.
a < x < b
Найпростіший спосіб запам’ятати є таким: забираємо праву частину подвійної нерівності й все, що залишилося записуємо як перше рівняння системи, для другого рівняння необхідно забрати ліву частину. Тобто будемо мати:
{/a < x/x < b
В такий спосіб розв’язуються подвійні нерівності, коли:
1. Змінна є не тільки у центральній частині:
В центральній частині є не лінійний вираз (змінна є у степені, під коренем, у знаменнику, під модулем і так далі):
З подвійною нерівністю так само як і зі звичайною нерівністю можна виконувати алгебраїчні дії, тобто, додавати, віднімати, множити, ділити і так далі.
Наприклад:
Знайти якщо
Нам необхідно орієнтуватися на результат який необхідно отримати В першу чергу подвійну нерівність необхідно помножити на (дії множення та ділення мають вищій пріоритет) щоб отримати В такому випадку кожна частина нерівності помножиться на
3 ∙ 2 < 2b < 9 ∙ 2
6 < 2b < 18
Тепер до всіх частин необхідно написати
6 - 7 < 2b - 7 < 18 - 7
-1 < 2b - 7 < 11
Подвійні нерівності можна додавати, віднімати, множити та ділити за такою схемою (знаки нерівностей мають бути однаковими).
Оцінка суми, різниці, добутку, частки:
Для всіх виразів вважаємо:
Сума та добуток чисел відносяться прямо
Різниця та частка чисел відносяться навхрест
Системи нерівностей
Раніше була розв’язана подвійна нерівність Уже відомо, що її можна переписати у систему нерівностей в такому вигляді:
{ 2 < (7 - 2x) : 3 (7 - 2x) : 3 ≤ 5
Системи нерівностей розв’язуються як окремі нерівності. Розв’язавши кожну з них будемо мати:
{ x < ½ x ≥ -4
Після чого необхідно нанести отримані нерівності на координатну пряму.
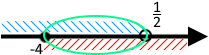
Наносимо на координатну пряму обидві нерівності. І відповіддю буде їх спільна частина.
-4 ≤ x < /1/2
x ∈ [-4; /1/2)