Ми вже розглядали з вами границю функції. За допомогою границі функції в точці можна знайти похідну функції.

Для цього вам необхідно скористатися формулою:

y' = ∆x#0/∆f/∆x = ∆x#0#f(x₀ + ∆x) - f(x₀)#∆x

Даний запис символізує похідну в точці.

Розберемося трішки детальніше. Побудуємо у прямокутній системі координат графік довільної функції «y = f(x)». На графіку поставимо дві точки. Точка «A(x₀; y₀)» буде не рухомою (зафіксованою), а точка «B(x; y)» може рухатися по графіку даної функції.

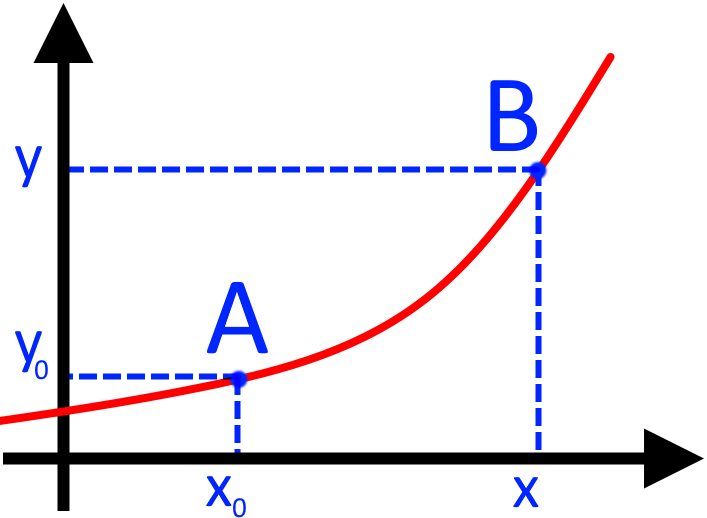
Різниця «x - x₀» називається приростом не залежної змінної або приростом аргументу функції. Дану різницю записують як «∆x» («∆» читаємо як «дельта»).

∆x = x - x₀

Відповідно, абсцису рухомої точки можна обчислити як:

x = ∆x + x₀

Схожа ситуація відбувається і з ординатою. Різницю «y - y₀» або «f(x) - f(x₀)» називають приростом функції у точці «x₀» та позначають «∆f». Дану різницю записують так:

∆f = f(x) - f(x₀)

Враховуючи, що «x = ∆x + x₀», то можна зустріти запис приросту функції у вигляді:

∆f = f(∆x + x₀) - f(x₀)

Відношення «/∆f/∆x» називають різницевим відношенням приросту функції до приросту аргументу даної функції.

/∆f/∆x = f(∆x + x₀) - f(x₀)∆x

Якщо, приріст аргументу функції спрямувати до нуля («∆x → 0»), то відношення «/∆f/∆x» буде рівне якомусь числу. Дане число буде похідною функції в точці «x₀».

f'(x₀) = /∆f/∆x = f(∆x + x₀) - f(x₀)∆x; при ∆x → 0

Або, це можна записати за допомогою границі функції:

f'(x₀) = ∆x#0#f(x₀ + ∆x) - f(x₀)#∆x

Функцію, яка має похідну в точці «x₀» називають диференційованою в цій точці.

Основні формули похідних

Для знаходження похідної є чимало готових формул. Розглянемо частину з них (в дужках ми напишемо особливі випадки певних формул):

C' = 0; C - const

(xⁿ)' = n∙x^{n - 1}; (x' = 1; (x)' = /1/2√x)

(a^x)' = a^x ∙ ln a; ((e^x)' = e^x)

(sin⁡ x)' = cos x

(cos x)' = -sin x

(tg x)' = 1cos² x

(ctg x)' = -1sin² x

(log_a x)' = /1/(x ∙ln a); ((ln x)' = /1/x)

Це є частина з основних формул похідних. Частіше за все ви будете зустрічати похідні з «добавками».

Правила обчислення похідних

Розглянемо основні правила обчислення похідних. Відразу зауважимо, що «f(x)», «g(x)» - функції, «k» - число.

1) Якщо ви маєте множення числа на функцію, то в такій ситуації дане число залишається без змін, а похідна береться виключно від функції:

(k ∙ f(x))' = k ∙ f'(x)

Наприклад, знайти похідну функції: «x⁴6».

На перший погляд вам може здатися, що тут не має ніякого множення функції на число. Але, ми можемо подати наявний дріб у вигляді множення дробів: «x⁴6 = /1/6 ∙ x⁴1». Пам’ятаємо, що чисельник множиться на чисельник, а знаменник на знаменник. Також, врахуємо, що будь-яке число помножене або поділене на «1» буде давати теж саме число. Тому, в кінцевому результаті, ми будемо мати такий вираз:

x⁴6 = /1/6 ∙ x⁴

А, цей вигляд цілком співпадає з виглядом формули «k ∙ f(x)». Обчислимо похідну даної функції. Тобто, матимемо запис:

(/1/6 x⁴)'

Пам'ятаємо, що коли функція множиться (або ділиться) на число, то похідна береться виключно від функції. А, число, залишається без змін.

(/1/6 x⁴)' = /1/6 ∙ (x⁴ )'

Тепер потрібно глянути на вигляд функції від якої беремо похідну. Ми маємо «x⁴», тобто, це є «x» в якомусь степені. Тому, нам підходить формула «(xⁿ)' = n ∙ x^{n - 1}». Отримаємо:

/1/6 ∙ (x⁴)' = /1/6 ∙ 4 ∙ x^{4 - 1} = /1/6 ∙ 4 ∙ x³

Даний вираз ми можемо спростити виконавши множення та скорочення.

/1/6 ∙ 4 ∙ x³ = 4x³6 = 2x³3

Отже, ми маємо такий результат похідної функції:

(/1/6 x⁴)' = 2x³3

2) Якщо ви маєте додавання/віднімання функцій, то в такому випадку ми беремо похідну від кожної функції.

(f(x) ± g(x))' = f'(x) ± g'(x)

Наприклад, знайти похідну функції: «1x³ + 3/x».

Отже, ми маємо додавання двох функцій від яких необхідно обчислити похідну. Пам’ятаємо, якщо в нас є додавання/віднімання декількох функцій від яких обчислюємо похідну, то потрібно обчислити похідну від кожної функції окремо:

(1x³ + 3/x)' = (1x³)' + (3/x)'

Але, якщо ви поглянете на формули для обчислення похідної, то там не буде формул у яких «х» є в знаменнику або під коренем. На справді ці вигляди є різновидом «змінної у степені». Тому, вам необхідно скористатися формулами степеня та кореня.

Скористаємося формулою степеня: «a^-n = 1aⁿ». В результаті отримаємо:

1x³ = x^-3

А, також, скористаємося формулою кореня: «maⁿ = an/m». В результаті отримаємо:

3/x = x 1/3

Отже, ми будемо мати такий вигляд функцій:

(1x³)' + (3/x)' = (x^-3)' + (x 1/3)'

Підбираємо формулу для обчислення похідної. Оскільки маємо «х» в степені, то підходить формула «(xⁿ)' = n ∙ x^{n - 1}». Матимемо:

(x^-3)' + (x1/3 )' = -3 ∙ x^{-3 - 1} + /1/3 ∙ x 1/3 ^{- 1} = -3x^-4 + /1/3 x^- 2/3

Залишається записати даний результат в кращому вигляді. Позбутися від «-» та дробу в степені. Знову скориставшись формулами: «a^-n = 1aⁿ», «maⁿ = an/m».

-3x^-4 + /1/3 x^- 2/3 = -3x⁴ + 23 3x²

3) Якщо ви маєте множення декількох функцій, то в такому випадку ми маємо брати суму похідну від кожної функції по черзі при цьому інші функції залишатимуться без змін в якості множників.

[f(x) ∙ g(x)]' = f'(x) ∙ g(x) + f(x) ∙ g'(x)

Наприклад, знайти похідну функції: «x⁵ ∙ 7^x ∙ sin ⁡x».

В даному випадку ми маємо множення декількох функцій. В цій ситуації варто похідну потрібно обчислювати як суму даних виразів в яких похідна береться від кожної функції по черзі. Оскільки, ми маємо три функції (три множники), то ми матимемо три доданки:

(x⁵ ∙ 7^x ∙ sin ⁡x)' = (x⁵ )' ∙ 7^x ∙ sin⁡ x + x⁵ ∙ (7^x)' ∙ sin ⁡x + x⁵ ∙ 7^x ∙ (sin⁡ x)'

Ви можете вираз від якого береться похідна записувати в кінці. Я ж демонструю що похідна йде послідовно по кожному множнику. Після чого вам залишається підібрати формулу по якій обчислюється похідна й обчислити її.

Для «x⁵» - «(xⁿ)' = nx^{n - 1}», «7^x» - «(a^x)' = a^x ∙ ln a», «sin ⁡x» - «(sin ⁡x)' = cos ⁡x». Отже, матимемо:

(x⁵)' ∙ 7^x ∙ sin⁡ x + x⁵ ∙ (7^x)' ∙ sin⁡ x + x⁵ ∙ 7^x ∙ (sin⁡ x)' = 5x⁴ ∙ 7^x ∙ sin⁡ x + x⁵ ∙ 7^x ln ⁡7 ∙ sin ⁡x + x⁵ ∙ 7^x ∙ cos⁡ x

Якщо буде необхідно, то виконуємо спрощення. Тобто, виконуємо додавання/віднімання/множення/ділення виразів.

4) Якщо ви маєте ділення функцій, то в такому випадку ми маємо брати похідну від чисельника помножену на знаменник відняти від похідної по знаменнику помножену на чисельник. При цьому знаменник піднімається до квадрату.

[/f(x)/g(x)]' = f'(x) ∙ g(x) - f(x) ∙ g'(x)[g(x)]²

Наприклад, знайти похідну функції: «ln xx⁴».

Отже, ми маємо ділення декількох функцій. В чисельнику ми маємо записати: похідну від чисельника помножену на знаменник, відняти похідну від знаменника помножену на чисельник; знаменник маємо підняти до квадрату.

(#ln⁡ x#x⁴)' = #(ln⁡ x)' ∙ x⁴ - ln ⁡x ∙ (x⁴)'#(x⁴)²

Залишається підібрати правильні формули для обчислення похідних. Для «ln⁡x» - «(ln x)' = /1/x», «x⁴» - «(xⁿ)' = nx^{n - 1}». Матимемо:

#(ln⁡ x)' ∙ x⁴ - ln ⁡x ∙ (x⁴)'#(x⁴)² = #/1/x ∙ x⁴ - ln⁡ x ∙ 4x³#(x⁴)²

Залишається спростити даний вираз.

#/1/x ∙ x⁴ - ln⁡ x ∙ 4x³#(x⁴)² = #x³ - 4x³ ∙ ln ⁡x#x⁸

Зверніть увагу, що в чисельнику ми маємо «x³», яке можна винести за дужки.

#x³ - 4x³ ∙ ln ⁡x#x⁸ = #x³(1 - 4 ln ⁡x)#x⁸

І ми маємо «х» в чисельнику та знаменнику, тому можна їх спростити за формулами степеня.

#x³(1 - 4 ln ⁡x)#x⁸ = #1 - 4 ln ⁡x#x⁵

При сильному бажанні або потребі ви можете продовжити спрощувати чисельник користуючись властивостями логарифмів.

5) Якщо ви маєте вкладену функцію (функцію в середині функції), то потрібно в першу чергу взяти похідну від зовнішньої функції помножену на похідну внутрішньої функції.

[f(g(x))]' = f'(g(x)) ∙ g'(x)

Наприклад, знайти похідну функції: «e^{3x + 5}».

Мабуть найскладніший варіант обчислення похідної це ситуація, коли у вас є складена функція.

Як зрозуміти, що функція є складеною? На справді доволі просто. Потрібно вивчити формули похідних. І якщо біля «х» ви бачите ще щось: «число» - «sin⁡ (x + 4)», «sin⁡ (2x)»; «степінь» - «2^x3»; «іншу функцію» - «(x - x²)³» тощо, то дана функція є складеною.

Наприклад, в нас є формула для обчислення похідної «(e^x)' = e^x», а в даному прикладі біля «х» ми маємо «щось» (числа). Тому, наша функція буде складеною.

Для обчислення похідної від складеної функції потрібно з першу взяти похідну від зовнішньої функції (вираз «без х») і помножити її на внутрішню функцію (вираз «з х»).

Зовнішня функція це функція яка знаходиться «найдальше» від «х». І при обчисленні похідної від зовнішньої функції ми можемо весь вираз «з х» вважати як якесь там «t».

Розглянемо нашу ситуацію:

(e^{3x + 5})' = (e^t)' ∙ (3x + 5)'

Зауважте, що в записі «e^t», «t» виступає замість «3x + 5». Я так написав, щоб вам легше було візуально сприймати запис похідної. Бо в іншому випадку це виглядало б так: «(e^{3x + 5})' = (e^{3x + 5} )' ∙ (3x + 5)'». А, це вже взагалі не зрозуміло, бо двічі повторюється «(e^{3x + 5})'».

Тому, ми з першу порахуємо похідну з «t», а потім повернемо все на свої місця.

Підбираємо формули і/та правила обчислення похідних для обчислення наявних похідних.

(e^t)' ∙ (3x + 5)' = e^t ∙ 3

Повертаємо на своє місце вираз «3x + 5». Остаточна відповідь буде:

(e^{3x + 5})' = 3e^{3x + 5}

Розглянемо складнішу ситуацію складеної функції. Обчислити похідну функції «sin²⁡(2x + 0,5)».

Як ви вважаєте, яка функція є зовнішньою? Якщо ви відповіли «квадрат», то повністю правильно! Чому? Ми можемо другий степінь винести за дужки:

sin²⁡ (2x + 0,5) = (sin⁡ (2x + 0,5))²

Зауважте, що квадрат знаходиться найдальше від «х». Саме, тому він є зовнішньою функцією. А, «sin⁡ (2x + 0,5)» буде внутрішньою функцією.

Спробуємо записати похідну функції:

[(sin ⁡(2x + 0,5))²]' = [t²]' ∙ (sin⁡(2x + 0,5))'

Зауважте, що ми замінили внутрішню функцію «sin⁡(2x+0,5)» на «t» для зручності обчислення похідної.

Похідна від «t²» буде:

[t²]' = 2t^{2 - 1} = 2t

І, якщо, повернутися до заміни, то матимемо:

2t => 2 sin⁡ (2x + 0,5)

Залишається обчислити похідну від «sin ⁡(2x + 0,5)». Але, зауважте, що тут також є складена функція! Де «sin» буде зовнішньою функцією, а «2x + 0,5» внутрішня. Чому? Бо біля «х» у вас знаходяться додаткові числа (функції). Тому, похідна буде такою:

(sin⁡(2x + 0,5))' = [sin ⁡t]' ∙ (2x + 0,5)'

Обчислимо похідну:

[sin ⁡t]' ∙ (2x + 0,5)' = cos⁡t ∙ 2 = 2 cos ⁡t

Повернемося до заміни:

2 cos⁡ t => 2 cos⁡ (2x + 0,5)

Тепер, повернемося до початкового прикладу та використаємо отримані результати:

[(sin⁡ (2x + 0,5))²]' = 2 sin⁡ (2x + 0,5) ∙ 2 cos⁡ (2x + 0,5) = 4 sin ⁡(2x + 0,5) · cos⁡(2x + 0,5)

Якщо скористатися формулою тригонометричних перетворень «2 sin⁡x · cos⁡x = sin ⁡2x», то отримаємо такий результат:

4 sin⁡(2x + 0,5) · cos⁡(2x + 0,5) = 2 sin⁡(2(2x + 0,5)) = 2 sin⁡(4x + 1)

Знаходження значення похідної в точці

Якщо вам необхідно обчислити похідну в точці, то в першу чергу потрібно обчислити похідну даної функції після чого підставити точку заміть змінної «х».

Наприклад, обчислити «f'(9)», якщо «f(x) = /x - 2/x + 1».

В першу чергу нам необхідно знайти похідну функції:

(/x - 2/x + 1)' = #(x - 2)'∙(x + 1) - (x - 2)∙(x + 1)'#(x + 1)² = #1∙(x + 1) - (x - 2)∙1#(x + 1)² = #x + 1 - x + 2#(x + 1)² = #3#(x + 1)²

Отже, ми знайшли похідну функції:

f'(x) = #3#(x + 1)²

Після чого залишається підставити значення «9» замість «х» та обчислити значення похідної функції.

f'(9) = #3#(9 + 1)² = #3#10² = #3#100 = 0,03

Обчислити значення похідної функції «y = #1#(2x-2)²» у точці «x₀ = 2».

Отже, нам необхідно в першу чергу обчислити похідну. Оскільки, тут є дріб, то можна скористатися формулами частки (ділення функцій) але враховуючи, що в чисельнику є «1», то можна перевернути знаменник і записати його у від’ємному степені. Після чого ви отримаєте складену функцію.

Скористаємося другим способом:

#1#(2x-2)² = (2x - 2)^{- 2}

Обчислимо похідну даної функції. Пам’ятаємо, що біля «х» ми маємо «щось», тому функція є складеною. Де степінь це зовнішня функція, а «2x - 2» внутрішня. Внутрішню функцію замінимо на «t».

[(2x - 2)^{- 2}]' = [t^{- 2}]'∙(2x - 2)' = -2t^{-2 - 1} ∙ 2 = -4 t^{- 3} = -#4#t³

Повернемося до заміни:

-#4#t³ => -#4#(2x - 2)³

y' = -#4#(2x - 2)³

Для обчислення значення похідної в точці нам залишається підставити замість «х» значення «2»:

y'= -#4#(2 · 2 - 2)³ = -#4#2³ = -/4/8 = -/1/2 = -0,5

Фізичний зміст похідної

В першу чергу нам варто розібратися з величинами які використовуються у фізичному змісті похідної. Це є:

Залежність даних функцій між собою записати за допомогою похідних таким чином:

V(t) = S'(t)

a(t) = V'(t) = (S'(t))'

Задача: Точка рухається прямолінійно за законом «S(t) = /2/3 t³ - 2t² + 4t» (час «t» вимірюється в секундах, шлях «S» - у метрах). Визначити прискорення його руху в момент «t = 10» с.

Щоб обчислити прискорення нам необхідно взяти похідну від швидкості. Але в нас не має швидкості. А, щоб знайти швидкість потрібно взяти похідну від відстані.

Отже, знайдемо в першу чергу похідну від відстані:

V(t) = S'(t)

Тобто, можемо записати:

V(t) = (/2/3 t³ - 2t² + 4t)' = /2/3 ∙ 3t² - 2 ∙ 2t + 4 = 2t² - 4t + 4

Тепер необхідно знайти прискорення. Для цього потрібно взяти похідну від швидкості:

a(t) = V'(t)

Матимемо:

a(t) = (2t² - 4t + 4)' = 2 ∙ 2t - 4 = 4t - 4

Залишилося знайти прискорення в момент часу «10» секунд. Для цього достатньо підставити значення в прискорення замість «t».

a(10) = 4 ∙ 10 - 4 = 36

Отже, прискорення в момент часу «10» секунд буде: «36 #м#с²».

Геометричний зміст похідної

Маючи рівняння функції ви можете побудувати його графік. З графіками функцій ви можете ознайомитися тут.

Зауважимо, що рівняння прямої має загальний вигляд:

y = kx + b

Де:

До даних графіків можна провести дотичну в певній точці. Рівняння дотичної до функції «f(x)» в точці дотику «x₀» можна записати за допомогою формули:

y = f'(x₀)(x - x₀) + f(x₀)

Де:

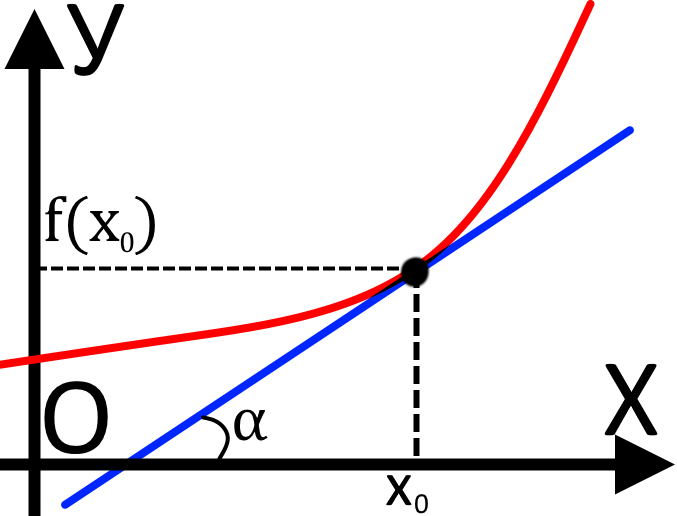
Зауважимо, що дотична до графіка функції має кут нахилу відносно додатного напрямку осі «ОХ». На графіку даний кут позначений як «α».

Значення похідної функції в точці дотику буде рівне кутовому коефіцієнтові, а також буде рівне тангенсу кута нахилу даної прямої:

f'(x₀) = k = tg α

Важливо розуміти, що дві прямі є паралельними, якщо їх кутові коефіцієнти рівні. Тобто, маючи дві прямі: «y₁ = k₁ x₁ + b₁», «y₂ = k₂ x₂ + b₂» вони будуть паралельні, якщо:

«k₁ = k₂», то «y₁ || y₂»

Дві прямі є перпендикулярними, якщо їх кутові коефіцієнти рівні але мають протилежні знаки. Тобто, маючи дві прямі: «y₁ = k₁ x₁ + b₁», «y₂ = k₂ x₂ + b₂» вони будуть перпендикулярні, якщо:

«k₁ = -k₂», то «y₁ ⊥ y₂»

Задача: обчисліть кутовий коефіцієнт дотичної, проведеної до графіка функції «f(x) = x² + /1/4 x⁴» у точці «x₀= -1».

Пригадаємо, що кутовий коефіцієнт дотичної («k») є рівний значенню похідної функції до якої проведена дотична в точці дотику («f'(x₀)»):

k = f'(x₀)

Отже, нам в першу чергу потрібно обчислити похідну:

(x² + /1/4 x⁴)' = 2x + /1/4 ∙ 4 ∙ x³ = 2x + x³

Маємо:

f'(x) = 2x + x³

Тепер, нам необхідно підставити замість «х» значення в точці дотику. Пам’ятаємо, що «x₀ = -1»:

f'(-1) = 2 ∙ (-1) + (-1)³ = -2 - 1 = -3

Отже, значення кутового коефіцієнту дотичної буде:

k = -3

Задача: Точка «А» лежить на параболі «y = 0,5x² - 6x + 1». Знайдіть координати точки «А», якщо дотична до параболи у точці «А» паралельна прямій «y = 4x + 5». Записати рівняння дотичної.

Отже, нам необхідно знайти координати точки «А» яка є точкою дотику параболи та прямої (дотичної до даної параболи). Позначимо дані координати так:

A(x₀; y₀); x₀, y₀ - ?

Нам відомо, що дотична є паралельною до прямої «y = 4x + 5». А, таке можливо лише, коли їх кутові коефіцієнти є рівними між собою. Тому, ми робимо висновок, що кутовий коефіцієнт дотичної є «4».

k = 4

Пригадаємо, що кутовий коефіцієнт дотичної («k») є рівний значенню похідної функції до якої проведена дотична в точці дотику («f'(x₀)»):

k = f'(x₀)

Зробимо висновок, що:

f'(x₀) = 4

В нас не відоме значення «f'(x₀)». Обчислимо похідну:

(0,5x² - 6x + 1)' = 0,5 ∙ 2 ∙ x - 6 = x - 6

Ми знайшли похідну функції:

f'(x) = x - 6

А, похідна в точці дотику (абсцисі) буде:

f'(x₀) = x₀ - 6

При цьому, ми можемо врахувати, що «f'(x₀) = 4». Матимемо:

x₀ - 6 = 4

x₀ = 10

Таким чином ми знайшли абсцису точки дотику. Для того щоб знайти ординату точки дотику потрібно значення «x₀ = 10» підставити у функцію або в рівняння дотичної. Але, оскільки ми не маємо рівняння дотичної, то підставимо у функцію:

f(x₀) = y₀ = 0,5 ∙ 10² - 6 ∙ 10 + 1 = -9

Отже:

A(x₀; y₀) = A(10; -9)

Для запису рівняння дотичної пригадаємо її формулу:

y = f'(x₀)(x - x₀) + f(x₀)

При цьому, ми вже знаємо:

x₀ = 10

f(x₀) = -9

f'(x₀) = 4

Матимемо:

y = 4(x - 10) - 9 = 4x - 40 - 9 = 4x - 49

Рівняння дотичної буде:

y = 4x - 49