Найпростіші тригонометричні рівняння
Поняття про arcsin (арксинус), arccos (арккосинус), arctg (арктангенс) і arcctg (арккотангенс) числа.
Відразу варто зауважити головний сенс у Ця функція перетворює число у радіальну (градусну міру). Вона просто запитує при яких радіанах (градусах) дана функція (тригонометрична функція) буде рівна числу «х».
Розглянемо все детально, але не варто це сильно завчати. В кінці виділимо необхідне. Також варто прочитати, що таке тригонометричні функції.
arcsin (арксинус) числа «а», де називають таке число (кут) з проміжку, синус якого дорівнює «а».
Позначають арксинус числа «а» так:
тоді коли:
Наприклад:
1. бо і
2. бо і
У випадках, коли є від’ємний кут, тоді будемо мати:
arcsin (-α) = - arcsin α
Наприклад:
бо і
arccos (арккосинус) числа «а», де називають таке число (кут) з проміжку, косинус якого дорівнює
Позначають арккосинус числа «а» так: Отже будемо мати:
тоді коли:
Наприклад:
1. бо і
2. бо і
У випадках, коли є від’ємний кут, тоді будемо мати:
arccos (-α) = π - arccos α
Наприклад:
бо і
Якщо є сума арксинуса та арккосинуса однакового кута то їх результат буде
arcsin x + arccos x = /π/2
arctg (арктангенс) числа «а», називають таке число (кут) з проміжку, тангенс якого дорівнює
Позначають арктангенс числа «а» так: Отже будемо мати:
тоді коли:
Наприклад:
1. бо і
2. бо і
У випадках, коли є від’ємний кут, тоді будемо мати:
arctg (-α) = - arctg α
Наприклад:
бо і
arcctg (арккотангенс) числа називають таке число (кут) з проміжку, арккотангенс якого дорівнює
Позначають арккотангенсом числа «а» так: «arcctg a». Отже будемо мати:
тоді коли:
Наприклад:
1. бо і
2. бо і
У випадках, коли є від’ємний кут, тоді будемо мати:
arcctg (-α) = π - arcctg α
Наприклад:
бо і
Якщо є сума арктангенса та арккотангенса однакового кута то їх результат буде
arctg x + arcctg x = /π/2
Отже. Після того як ми розібралися з тригонометричних функцій залишилося зрозуміти навіщо він нам необхідний.
Для цього розглянемо графіки тригонометричних функцій.
(зауважте, ця функція не виходить за межі
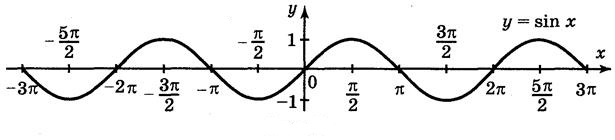
(зауважте, ця функція не виходить за межі
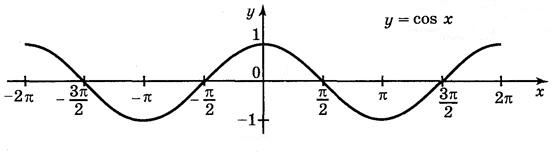
tg x:

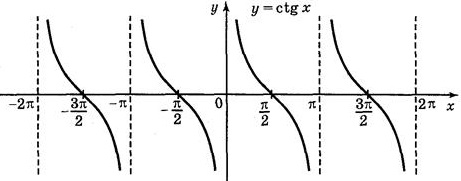
ctg x:
Коли ми маємо тригонометричне рівняння вигляду: То це означає, що ми маємо горизонтальну пряму (вона є паралельною до осі яка проходить через точку
Наприклад, тригонометричне рівняння
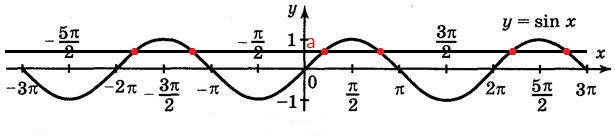
Отже, коли у нас є тригонометрична функція яка рівна якомусь числу, то такий запис називається «тригонометричним рівнянням».
Наприклад:
Розв’язати тригонометричне рівняння, означає «знайти усі точки перетину прямої та графіку тригонометричної функції».
На прикладі точки перетину функції та прямої «a» виділені червоним кольором.
Оскільки, кожна з функцій є безмежна та періодична та пряма «а» є безмежною, то таких точок буде безліч. Щоб не перераховувати кожну з цих точок є виведені спеціальні формули де застосовується
Тригонометричне рівняння, типу
Відразу зауважимо, що у випадках, коли або то рівняння розв’язків не має.
Є три варіанти стандартного розв’язання такого рівняння.
Якщо, то розв'язок буде таким:
x = -/π/2 + 2πn, n ∈ Z
Якщо, то розв'язок буде таким:
x = πn, n ∈ Z
Якщо, «sin x = 1» (а = 1), то розв'язок буде таким:
x = /π/2 + 2πn, n ∈ Z
У випадках, коли будемо мати такий розв’язок:
У випадках, коли будемо мати такий розв’язок:
Наприклад:
1. sin x = /√2/2
В першу чергу перевіряємо чи підходить значення якому рівний синус по обмеженню: Все добре. Оскільки це значення не є стандартним, то ми використовуємо загальну формулу:
Тепер необхідно знайти arcsin. Будемо мати: Отримаємо остаточну відповідь:
2. 2sin x + 1 = 0
Тут в першу чергу необхідно звести рівняння до правильного вигляду: Для цього перенесемо «1» в протилежну частину. Та поділимо на «2», що стоїть з синусом.
2sin x = -1
sin x = -/1/2
Виконаємо перевірку: Все добре. Але через те, що ми маємо від’ємне число, то нам необхідно скористатися другою стандартною формулою (для запису від’ємних чисел).
Тепер необхідно знайти arcsin. Будемо мати: Отримаємо остаточну відповідь:
Тригонометричне рівняння, типу
Відразу зауважимо, що у випадках, коли або то рівняння розв’язків не має.
Є три варіанти стандартного розв’язання такого рівняння.
Якщо, то розв'язок буде таким:
x = π + 2πn, n ∈ Z
Якщо, то розв'язок буде таким:
Якщо, то розв'язок буде таким:
x = 2πn, n ∈ Z
У випадках, коли будемо мати такий розв’язок:
У випадках, коли будемо мати такий розв’язок:
Наприклад:
1. cos x = /√2/2
Перевіряємо чи дане рівняння має розв’язки. отже рівняння має розв’язки. Скористаємося загальною формулою:
Знайдемо arccos:
2. 2cos x + √3 = 0
У цьому випадку як і у випадку з синусом необхідно звести рівняння до стандартного вигляду: Для цього перенесемо в іншу сторону та поділимо на
2cos x = -√3
cos x = -/√3/2
Тепер необхідно перевірити чи рівняння має розв’язки: Розв’язки є, але оскільки число є від’ємним, то варто скористатися другою стандартною формулою:
З’ясуємо значення арккосинуса:
Тепер залишається лише порахувати вираз у дужках. Оскільки там є дріб скористаємося правилом віднімання дробів (дробу та числа). Детальніше читайте у розділі «Алгебраїчний дріб».
Будемо мати:
Тригонометричне рівняння, типу
Якщо, то розв'язок буде таким:
x = πn, n ∈ Z
У випадках, коли будемо мати:
У випадках, коли будемо мати:
Наприклад:
1. tg x = √3
Тангенс та котангенс обмежень не мають. Тому не потрібно робити перевірок.
2. 4√3 ∙ tg x + 4 = 0
Необхідно звести рівняння до стандартного вигляду Для цього перенесемо в протилежну сторону та поділимо на що знаходяться біля тангенсу. Будемо мати:
4√3 ∙ tg x = -4
tg x = -/4/4√3
tg x = -/1/√3
Тригонометричне рівняння, типу
Якщо, то розв'язок буде таким:
У випадках, коли будемо мати:
У випадках, коли будемо мати:
1. ctg x = √3
Тангенс та котангенс обмежень не мають. Тому не потрібно робити перевірок.
2. 2ctg x + 2√3 = 0
Необхідно звести рівняння до стандартного вигляду Для цього перенесемо в протилежну сторону та поділимо на що знаходяться біля котангенсу. Будемо мати:
2ctg x = -2√3
ctg x = -/2√3/2
ctg x = -√3
Часто доводиться зустрічати приклади, коли «х» є не сам. Тобто може бути такий вигляд: В таких випадках вважають одним цілим і просто записують замість як в попередніх прикладах. Після чого необхідно знайти
Варто зауважити. У випадках коли до щось додається або віднімається, то при перенесені в протилежну сторону (коли шукаємо не потрібно нічого додавати/віднімати.
Наприклад:
Як ми вже знаємо в першу чергу необхідно звести приклад до стандартного вигляду
Хоча в дужках є але ми все одно вважаємо його як одне ціле яке будемо писати замість Отже будемо мати:
/x/4 - /π/3 = (-1)n arcsin /√3/2 + πn, n ∈ Z
/x/4 - /π/3 = (-1)n arcsin /π/3 + πn, n ∈ Z
Тепер необхідно забрати у протилежну сторону від Не забуваємо, що при перенесені у протилежну сторону знак змінюється на протилежний. Будемо мати:
Варто зауважити, що у випадках коли ви маєте щось біля (наприклад: то не потрібно нічого додавати/віднімати. Тобто все залишиться як є.
Тепер необхідно позбутися у знаменнику. Для цього помножимо весь вираз на Будемо мати:
Це вже і є розв’язок.
Часто бувають ситуації, коли є не першим в дужках.
Наприклад:
В таких прикладах варто зробити змінну першою.
Тобто:
Після чого, варто позбутися мінуса біля
Для цього його необхідно винести за дужки:
Тепер варто скористатися правилами винесення з під тригонометричної функції (властивості парних та не парних функцій).
Нагадаємо:
sin(-x) = - sin x
cos(-x) = cos x
tg(-x) = - tg x
ctg(-x) = - ctg x
Детальніше читайте тут.
В нашому випадку будемо мати:
sin(-(x - π)) = - sin(x - π)
Після чого розв’язуємо як попередній приклад.
Приклад: tg (/π/4 - /x/2) = -1
Як видно стоїть другим ще й зі знаком Тому ми відразу винесемо за дужки:
tg(-(/x/2 - /π/4)) = -1
«tg» це не парна функція, тому від аргументу виноситься на перед:
- tg(/x/2 - /π/4) = -1
Залишилося звести до стандартного вигляду: Для цього варто позбутися Просто змінимо знаки у нашому рівнянні (помножимо все рівняння на
tg(/x/2 - /π/4) = 1
Помножимо на «2» для того щоб позбутися знаменника біля
x = π + 2πn, n ∈ Z